一类含不定非线性项奇异椭圆方程的正解

吕登峰

一类含不定非线性项奇异椭圆方程的正解

吕登峰

(孝感学院数学系,湖北孝感432000)

研究了一类含Sobolev-Hardy临界指数与不定非线性项的奇异椭圆方程,通过Nehari流形和精确的能量估计,运用集中紧性原理与强极值原理得到了这类方程正解的存在性.

正解;Sobolev-Hardy临界指数;椭圆方程

0 引言及主要结果

本文研究如下奇异椭圆方程正解的存在性

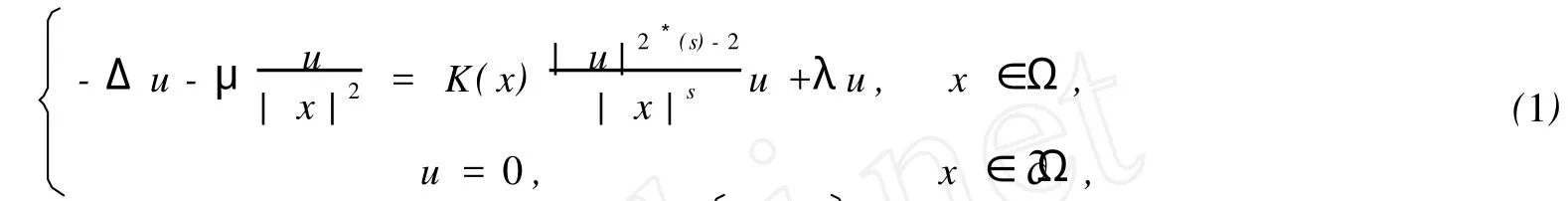
其中Ω⊂RN(N≥5)是包含原点的有界光滑区域是Sobolev-Hardy临界指数,λ>0.

当K(x)≡C时,已有许多这类问题解的存在性结果,如当K(x)≡1,s=0时,Jannelli在文[1]中给出了方程(1)在H10(Ω)中至少有一个正解,Ferrer和Gazzola在文[2]、Shen和Yang在文[3]中证明了方程(1)非平凡解的存在性,Chen在文[4]中证明了方程(1)多重解的存在性;当λ=0时,Deng和Jin在文[5]中证明了方程(1)G-对称解的存性.本文对更一般形式的K(x)给出方程(1)正解的存在性.我们设K(x)满足如下条件:

(A1)K(x)∈L∞(Ω),K+(x)=max{-K(x),0}≠0,K-(x)=max{-K(x),0}≠0;

(A2)KM:=supx∈¯Ω|K(x)|=K(0)>0,且存在δ>0,使得对于x∈B2δ(0),有K(0)-K(x)=O(|x|α),其中

用H10(Ω)表示通常的Sobolev空间,其等价模定义为表示H10(Ω)的对偶空间,用C或Ci等表示正常数,它们在不同的行或段落中可以不同,用→(⇀)表示在相应空间中的强(弱)收敛,O(εt)表示|O(εt)|/εt≤C,o(εt)表示ε→0时,|o(εt)|/εt→0.定义H10(Ω)上的能量泛函

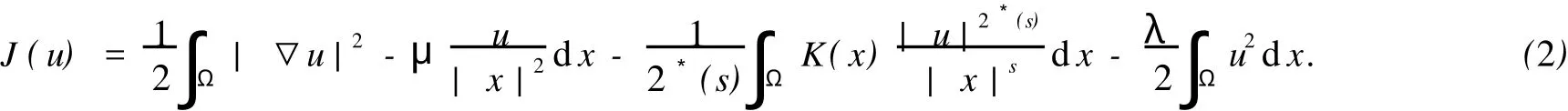
由Hardy不等式,Hardy-Sobolev不等式与K(x)满足的条件可知J(u)∈C1(H10(Ω),R),称u∈H10(Ω)是方程(1)的弱解当且仅当对任意的φ∈H10(Ω),有

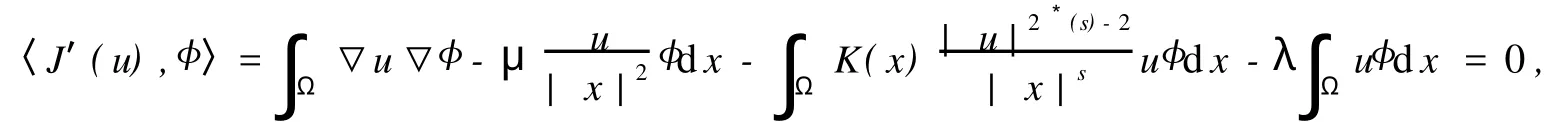
因而其弱解恰好是能量泛函J(u)在H10(Ω)上的临界点.定义最佳Sobolev-Hardy常数

由文[6]知Sμ的达到函数

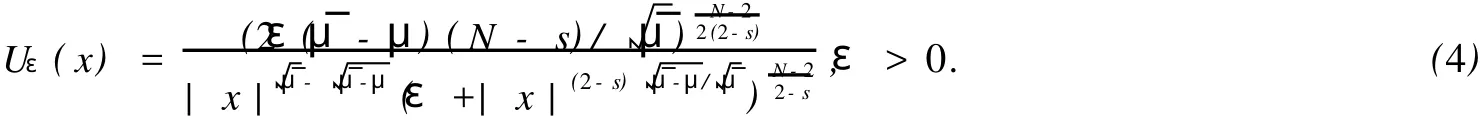
而且Uε(X)是方程的解,并满足

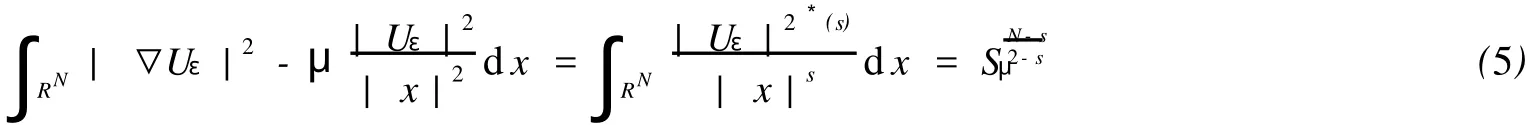
设B2δ(0)={x∈RN,|x|<2δ}⊂Ω.定义截断函数φ(x)∈C∞0(Ω,[0,1]),使得当x∈Bδ(0)时,φ(x)=1当x∈ΩB2δ(0)时,φ(x)=0,且对于任意x∈Ω,|▽φ|≤C.

本文的主要结果可表述为下面的定理.

定理1 若条件(A1),(A2)成立,且λ∈(0,λ1),μ∈(0,¯μ-1),则方程(1)至少存在一个能量水平于(0,的正解.

1 主要结果的证明

引理1 记uε=jφUε,则在定理1的条件下,有

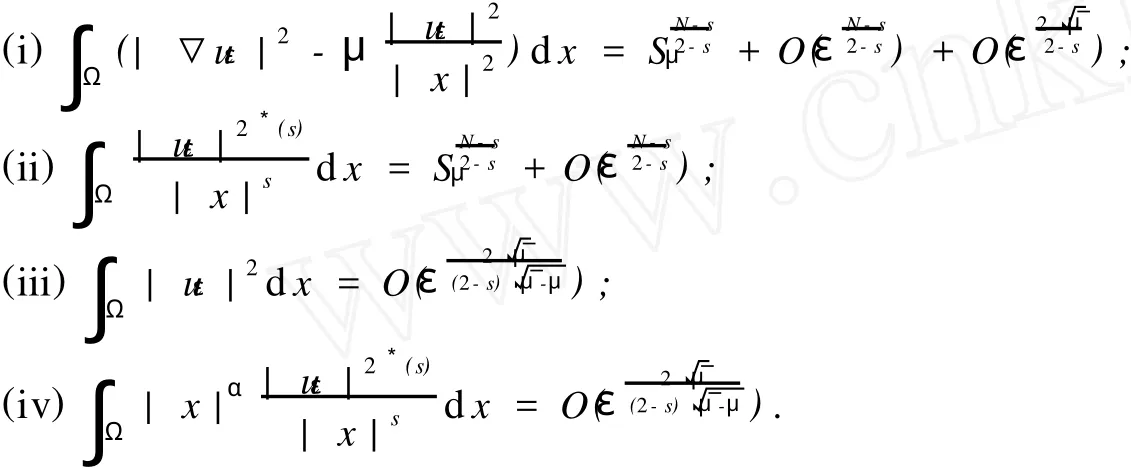
证明 由文[3],或[6,7]类似易得.

定义Nehari流形M={u∈H10(Ω):G(u)=〈J′(u),u〉=0,u≢0}.由M的定义知,对任意u∈N,有

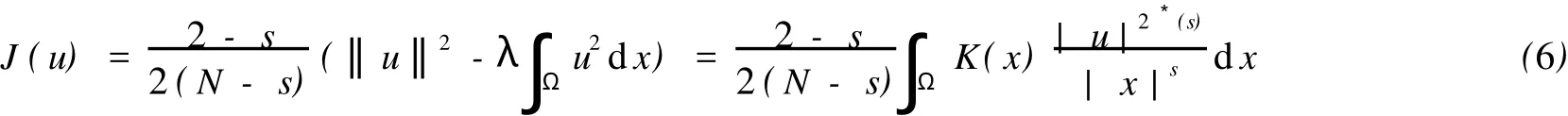
引理2 存在ρ>0,使得对任意u∈M,有‖u‖≥ρ.

证明 对u∈M,由式(6)与(A2)有,

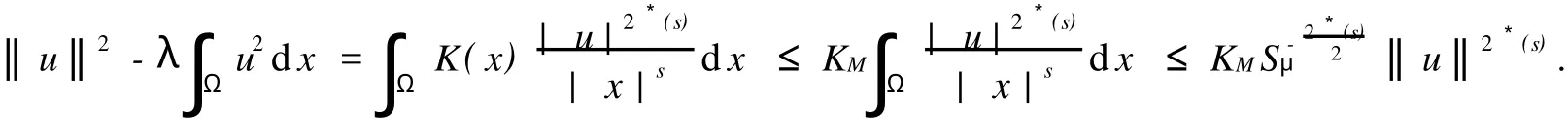
因此,由Sobolev不等式有

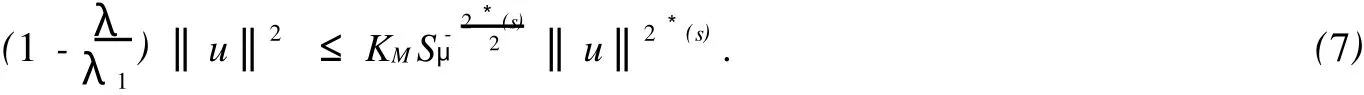
从而由式(7)有

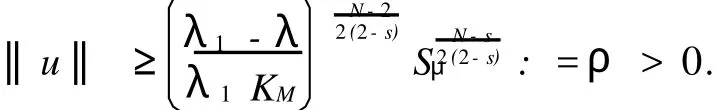
引理3 存在序列{un}⊂M,使得J(un)→c,J′(un)→0在H-1(Ω)中.{～un}⊂M为一相对于c=J(u)的极小化序列,由Ekeland变分原理,可找到序列{un}⊂{～un}⊂M,使得J(un)→c,J′(un)|M→0.又由Lagrange乘子法知,存在rn,使得

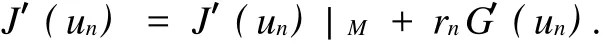
而J′(un)|M→0,所有有J′(un)-rnG′(un)→0,进而有

由M的定义知

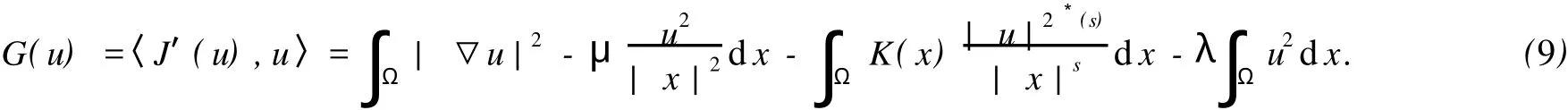
则由式(9),(6)及引理2有

由un∈M知〈J′(un),un〉=0,再结合(8),(10)式知rn=0,从而引理3得证.

引理4 设{un}⊂M,满足J(un)→c,J′(un)→0在H-1(Ω),则{un}在H10(Ω)中必有一个强收敛的子列.

证明 由{un}⊂M,J(un)→c,0<λ<λ1知,

因此,{un}在H10(Ω)中有界.故可选取子序列不妨仍记为{un},使得当n→∞时,有un⇀u在H10(Ω)中;un→u,a.e.于Ω;由文[8]集中紧性原理知,存在至多可数集I,使得

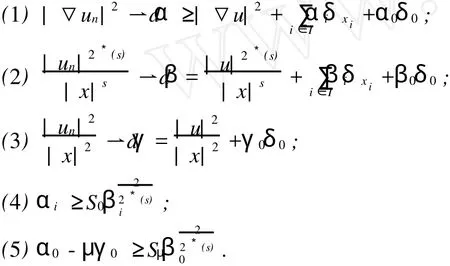
取截断函数φi=1,当|x-xi|≤r时;φi=0,当|x-xi|≤2r时,令ψi=unφi.由〈J′(un),ψi〉=o(1)‖ψi‖可得

令n→∞有,αi≤K(xi)βi≤KMβi,再结合(4)有(a)βi=0,或

若存在i∈I,使得βi≠0,即(b)发生,则由测度β的有界性知,集I必为有限的,再利用Brezis-Lieb引理(文[9])有

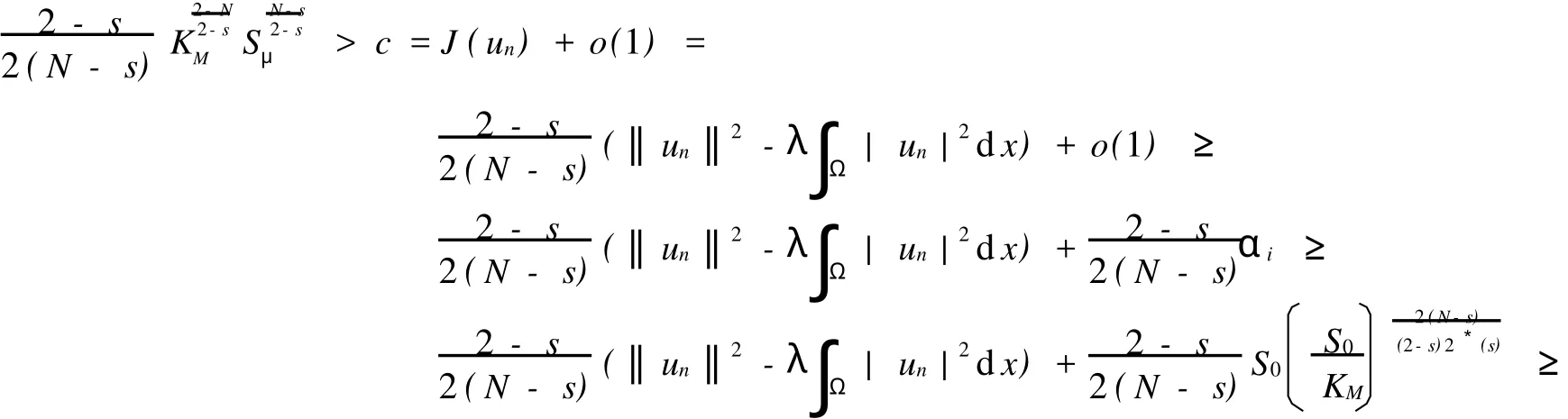
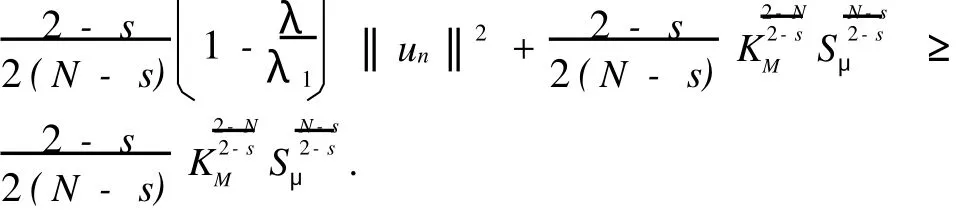
矛盾.所以,对任意i∈I,βi=0.

取截断函数φ0=1,当|x|≤r时;φ0=0.当|x|≥2r时;令ψ0=unφ0.由〈J′(un),ψ0〉=o(1)‖ψ0‖可得

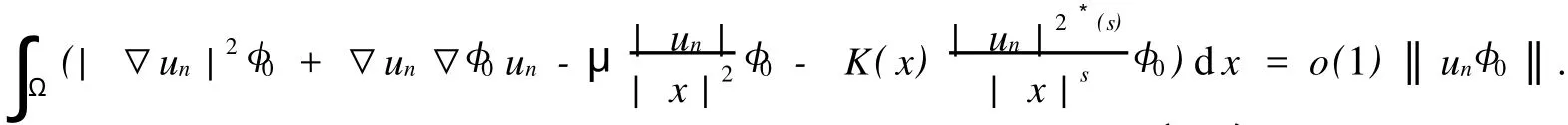
令n→∞,r→0有,α0-μ γ0≤K(0)β0≤KMβ0,再结合(5)有.同理可证集中在0点不可能发生,即β0=0.因此对任意i∈I,β0=βi=0.从而un→u在H10(Ω)中.

证明 取t0uε∈M,则

由引理1与(12),(A2)可得

从而

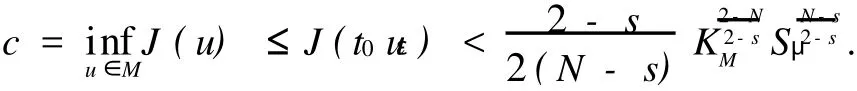
定理1的证明 由引理2-5可知,存在u0∈M达到c.由于若{un}是J(u)在M上的极小化序列,则{| un|}也是,故可设u0为非负临界点,即u0为方程(1)的一个非负解,再由强极值原理知u0为方程(1)的正解.

[1] JANNELLI E.The Role Played by Space Dimension in Elliptic Critical Problems[J].J Dif f erential Equations,1999, 156:407-426.

[2] FERRER A,GAZZOL F.Existence of Solutions for Singular Critical Growth Semilinear Elliptic Equations[J].J Dif f erential Equation,2001,177:494-522.

[3] SHEN Z,YANG M.Nontrivial Solutions for Hardy-Sobolev Critical Elliptic Equations[J].Act Mathematica Sinica,Chinese Series,2005,48:999-1010.

[4] CHEN J.Multiplicity Result for A Singular Elliptic Equation with Indefinite Nonlinearity[J].J Math A nal A ppl,2008, 337:493-504.

[5] DENG Y,J IN L.On Symmetric Solutions of A Sigular Elliptic Equation with Critical Sobolev-Hardy Exponent[J].J Math A nal A ppl,2007,329:603-616.

[6] KANG D,PENG S.Positive Solutions for A Singular Critical Elliptic Problem[J].A pplied Mathematics Letters,2004,329:603-616.

[7] CHEN J.Existence of Solutions for a Nonlinear PDE with an Inverse Square Potential[J].J Dif f erential Equations, 2003,195:497-519.

[8] LIONS P L.The Concentration Compactness Principle in the Calculus of Variations,the Limit Case,I,II[J].Rev Mat Iberoamericane,1985,1:145-201,45-121.

[9] BREZIS H,LIEB E.A Relation Between pointwise Convergence of Functions and Convergence of Integrals[J].Proc A mer Math Soc,1983,88:486-490.

[10] WILL EM M.Minimax Theorems[M].Boston:Birkhäuser,1996.

Positive Solution for Singular Elliptic Equations with Indefinite Nonlinearity

LÜDeng-feng
(Department of Mathematics,Xiaogan University,Xiaogan432000,China)

A class of singular elliptic equations with Sobolev-Hardy critical exponent and indefinite nonlinearity term is studied.With Nehari manifold and delicate energy estimates,the existence of positive solution is obtained by concentration-compactness principle and strong maximum principle.

positive solution;Sobolev-Hardy critical exponent;elliptic equation

O175.25

A

0253-2395(2010)03-0321-05

2009-11-27;

2010-02-07

国家自然科学基金重点项目(10631030);湖北省教育科学“十一五”规划(2007B086)

吕登峰(1981-),男,湖北洪湖人,助教,硕士,主要研究领域:偏微分方程.E-mail:dengfeng1214@163.com