千岛湖南浦大桥地震响应研究

刘明艳，李自林，李 妲，郭晓刚

(1. 天津城市建设学院 土木工程系，天津 300384；2. 河海大学 港口海岸与近海工程学院，南京 210098；3. 天津市纳川建筑设计有限公司 结构室，天津 300384)

钢管混凝土拱桥以其主拱圈形式为划分依据，可分为肋式和桁式(格构式)两种，桁式拱肋也称为格构式.考虑到钢管对混凝土的套箍作用以及拱桥的受力特点，可采用较小的钢管直径而取得较大的抗弯刚度，且杆件以受轴向力为主，这与拱桥的受力特性相符.近年来，我国所建的多肢桁式钢管混凝土拱桥大多为拱肋弦杆采用钢管混凝土截面[1-4]，而腹杆和平联均采用钢管，这样减少了钢材和混凝土的用量，从而在自重方面有很大的优势，其跨越能力也相应增强.另外，各肢受轴向力为主，更适于依据钢管混凝土套箍作用理论进行设计计算.本文以千岛湖南浦大桥为例，应用动态时程分析法，研究该桥在地震荷载作用下的动力响应.

1 工程概况

千岛湖南浦大桥总设计长度 330 m，拱轴为悬链线，拱轴系数为 1.167，净矢高为 55.99 m，净跨径为307.94 m，矢跨比为 1/5.5.主拱圈钢管外径为 850 mm，上弦杆及下弦杆中间段壁厚为12 mm，下弦杆拱脚段局部加厚为 20 mm，中间增设过渡段壁厚为14 mm.直腹杆断面处设置 16号槽钢组成的剪刀撑.肋间设置13道双“K”字型钢管风撑，拱顶设置一道，两边各设置六道，水平间距 20 m.吊杆采用热挤PE护套防护的镀锌高强钢丝PES(C)7-055，吊杆锚头为冷铸墩头锚.横梁及桥台处共设 52处四氟滑板橡胶支座，另设八处横向限位液压滑动支座.仅在桥台处设SSFB-160型桥面板伸缩缝，桥面宽13 m.

吊杆横梁上设置“T”型预应力混凝土桥面板，横向桥面板之间现浇接头，纵向桥面板在吊杆横梁处现浇接头，形成全桥连续的纵横正交梁格体系，在二期恒载及活载作用下为多点弹性支撑连续梁受力体系.吊杆横梁采用的预应力钢绞线为符合美国ASTM A416—97规定的270级高强低松弛钢绞线.

2 有限元模型的建立

应用大型有限元分析软件 MIDAS/Civil建立全桥模型，拱肋、桥面系及风撑采用梁单元模拟，吊杆采用桁架单元模拟.该桥两边桥台为耳墙式重力桥台，拱肋与桥台连接处为固定端约束.全桥 2432个节点，5378个单元，有限元模型如图1所示.

拱肋及腹杆等截面为钢管与混凝土两种材料组合而成的复合截面.为达到对原桥更准确的模拟，需要将钢材与混凝土等效成一种各向同性的材料，即按下式将原钢管混凝土截面换算成等效截面[1]，换算截面的抗压刚度(EA)及抗弯刚度(EI)分别为

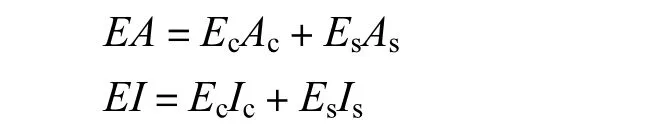
式中：Ec，Ac，Ic分别为混凝土的弹性模量、截面积、截面惯性矩；Es，As，Is分别为钢管的弹性模量、截面积、截面惯性矩.

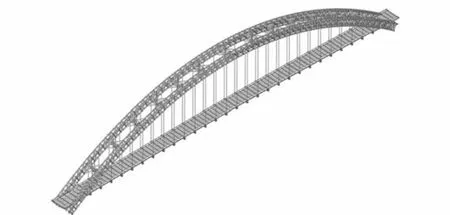
图1 结构有限元模型

此种等效截面的计算方法使设计计算简化，但不能考虑钢管对混凝土的套箍作用，因此在钢管混凝土拱桥的设计计算中是比较保守的计算方法.

3 有限元分析

3.1 自振特性分析

要进行抗震分析，首先要计算结构的动力特性，将结构离散化为空间有限元模型.为了使各个方向的振型参与质量都达到 90%以上，计算结构自振前300阶模态.其中前10阶振型特征见表1，结构前10阶振型见图2.

表1 模型前10阶自振特性

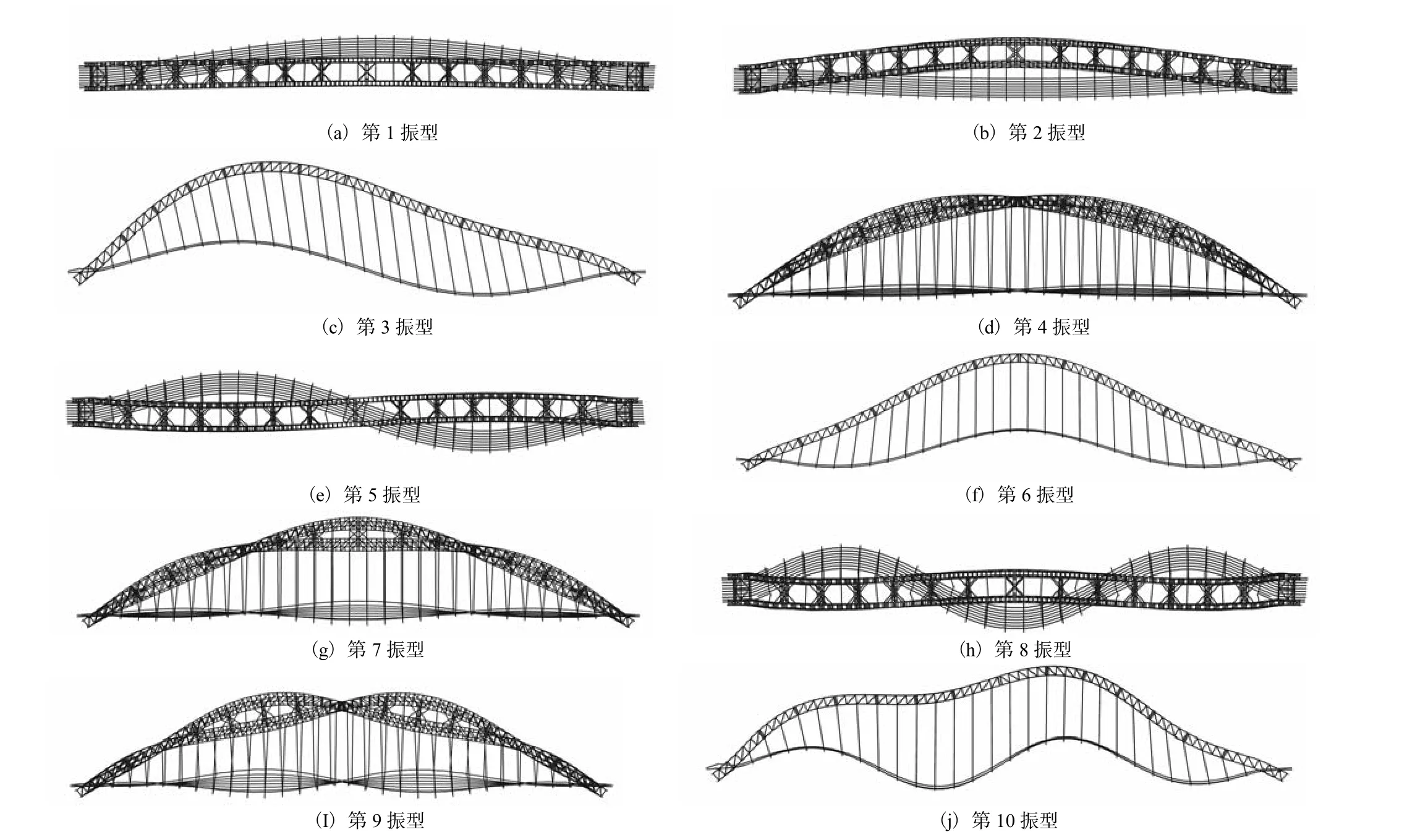
图2 结构前10阶振型图

由该桥的振型与周期可以得出如下结论：

(1)结构第一振型周期为3.85 s较大，可以看出该桥梁结构较柔.第一振型为桥面系的一阶弯曲，是因为桥面系与横梁之间的联系较弱，导致桥面系横向约束小，桥面系虽然不属于整体受力体系，但是却成为全桥最柔的部分，占据了主振型的位置；

(2)第二振型为主拱肋的一阶弯曲，周期为 3.25 s，仍然较大，说明全桥受力体系属于柔性结构.虽然主拱肋采用多肢桁式以及肋间横撑的设计对结构的抗扭转能力和横向刚度有很大的贡献，但该桥梁跨径太大，横向刚度相对较小是不可避免的；

(3)前三阶模态以桥面系、拱肋的面内弯曲为主，第四振型才出现扭转，说明该桥的抗扭刚度较好.该桥拱肋为四肢桁式，为提高结构的抗扭刚度做出了很大的贡献；

(4)该桥梁前 10阶振型中，结构侧向弯曲、竖向弯曲和扭转的比例相对较均衡，说明该结构整体受力体系合理.

3.2 动态时程分析

该桥净跨 308 m，属特大桥，如果采用反应谱法计算其地震响应，由于两桥台间距太大，在实际地震作用下与反应谱法假设两桥台同时受到激励的理论不相符合，所以选用时程分析方法[5].

在地震波的选取上，依据该桥所处 2类场地，杭州千岛湖地区抗震设防烈度为6度，按7度进行抗震设计[6]，选用国际应用较广泛的 EI-centro波，计算时间 30 s，时间步长 0.02 s，共计算 3000步.考虑纵向、横向、竖向三个方向的地震作用.结构在纵向、横向与竖向地震作用下各控制截面的位移和内力见表2、表 3.

表2 三个方向地震波作用下结构控制截面的位移 mm

表3 三个方向地震波作用下结构控制截面的内力

由表2、表3可得出：结构在横向地震作用下的位移和内力最大，这与结构自振特性中所表现出的横向刚度较小相符合.竖向地震作用下结构的位移较小，但内力较大，超过了纵向地震作用的影响，不可忽略.

由以上数据显示竖向地震作用不可忽略，因此考虑纵向＋横向地震作用和纵向＋横向＋竖向地震作用两种工况，对原结构重新输入地震作用，并将计算结果列于表4、表5中.

表4 按原角度输入地震波后结构各控制截面的位移 mm

表5 按原角度输入地震波后结构各控制截面的内力

关于地震波的输入方向问题，以上所做的研究均按照纵向地震作用对应结构的纵向、横向地震作用对应结构的横向的规则进行地震波的输入.但现实条件中，地震作用不可能严格按照此种情况发生.所以考虑将原纵向、横向地震波的输入方向旋转 90°后再对原结构进行激励，即原纵向地震波对应结构的横向输入，原横向地震波对应结构的纵向输入.计算结果列于表6、表7中.

表6 按90°输入地震波后结构控制截面的位移 mm

表7 按90°输入地震波后结构控制截面的内力

将地震波的输入角度旋转 90°后，结构各控制截面的位移和内力有很大变化，而且这些变化无一定的规律性可言.因此，设计时应考虑地震波的输入方向不同所产生的影响，要得到最不利输入方向还需做更深一步的研究.另外，由表6、表7可发现，两种工况下结构的反应差别并不是很大，即竖向地震作用的参与与否对结构的位移和内力影响很小，这与不同方向输入状态下竖向地震作用不可忽略的结论相矛盾.

目前，大多数地震响应分析的研究都没有考虑到地震波输入方向的问题，但此方面的缺陷已显示出来，预计日后规范中会增加相关方面的条文规定，以使结构地震响应的研究能取得更准确的结果.

4 结 论

(1)该结构自振周期较大，体系偏柔；前 10阶振型中包括结构侧弯、竖弯和扭转；由于拱肋形式为四肢桁式，且肋间设置横撑使结构的抗扭转刚度较好.但该桥梁跨度很大，且为单跨结构，导致横向刚度很弱，建议增强主拱肋结构的横向刚度，或减小跨度采用两跨或多跨的形式来改善横向刚度偏小的情况.另外，桥面系的横向约束也应适当增加.

(2)竖向地震作用对结构的影响不能忽略，这符合规范要求特大桥梁必须做竖向地震分析的规定.

(3)改变地震波的输入角度后，结构的位移和内力有很大变化，但无一定的规律性，可知按结构纵向、横向输入纵向、横向地震波的方式不一定为最不利输入状态.但当前大多数研究均默认采取此种方式输入地震波，因此建议在研究地震响应分析时，应考虑最不利输入方向的问题.

［1］陈宝春. 钢管混凝土拱桥设计与施工[M]. 北京：人民交通出版社，1999.

［2］王建军，谢开仲，秦 荣. 大跨度钢管混凝土提篮拱桥地震反应分析[J]. 武汉理工大学学报，2009，33(2)：365-368.

［3］李广慧，李小军，李胜利. 中承式钢管混凝土拱桥的地震响应分析[J]. 应用基础与工程科学学报，2009，17(1)：144-151.

［4］张 波，李术才，杨学英. 上承式大跨度钢管混凝土拱桥地震反应分析[J]. 公路交通科技，2009，26(3)：64-67.

［5］范立础. 桥梁抗震[M]. 上海：同济大学出版社，1997.

［6］JTJ 004—2005，公路桥梁抗震设计规范[S].