某类柯西变换的零点分布情况
李红光
(怀化学院数学系,湖南怀化 418008)
某类柯西变换的零点分布情况
李红光
(怀化学院数学系,湖南怀化 418008)
假设是由压缩映射Sj(z)=εj+ρ(z-εj)组成的迭代函数系 (IFS),其中ρ为压缩比,且满足0<ρ<ρm(m ≥4,ρm的定义见[1])是的吸引子,μ是支撑在K上的Hausdorff测度.最近,文 [1]中讨论了自相似测度的柯西变换在|z|>1内的罗朗系数.文章主要研究zw)-1dμ(w)在其解析范围内的零点分布情况.
零点; Hausdorff测度; 吸引子
1 引 言
近年来,文献 [1],[2]和 [3]中讨论了自相似测度柯西变换在|z|>1内的罗朗系数及矩的估计,后者在物理领域内有较为广泛的应用.
假设{Sj}m-1j=0是由压缩映射

组成的迭代函数系 (IFS),其中

2 柯西变换的零点分布
证明 显然 G(z)在|z|<1内解析,因此在|z|<1内有泰勒展开

由 (2.1)和μ的旋转不变性,有
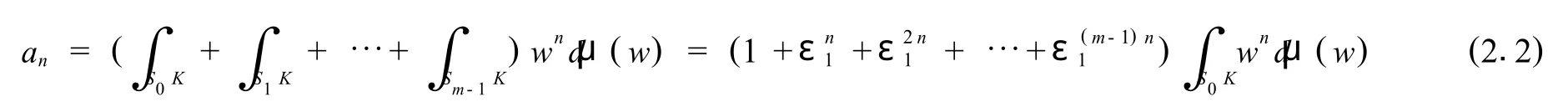
由 [1]中定理5.2知,
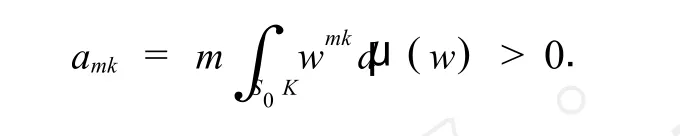
因此引理得证.
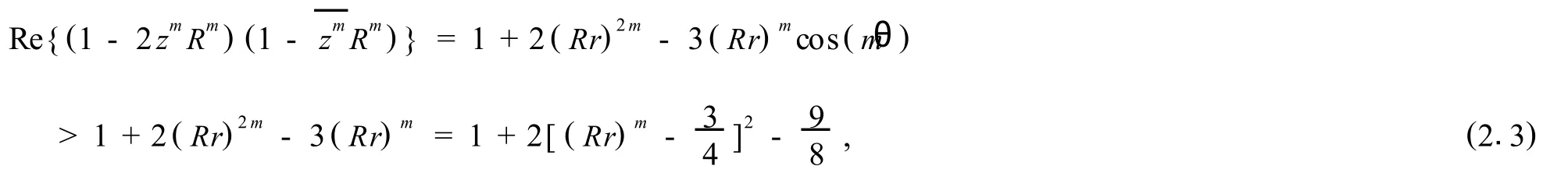
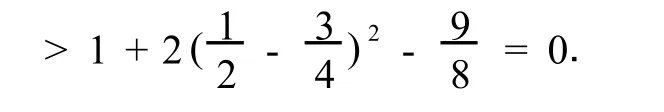
因此引理得证.
证明 因为 G(z)在|z|<1内解析,因此在|z|<1内有泰勒展开

令f(z)=1和记|z|= R,由引理1我们有
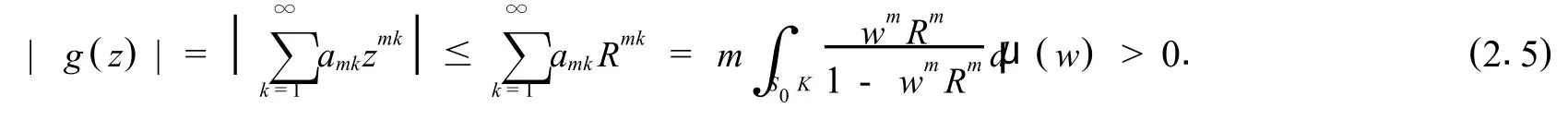
因此有

注意到μ(1)=0,因此在(2.6)中的积分区域S0K中除去1,并不影响其结果.
因此,由引理2知对w∈S0K,且,有(2.6)大于零.
[1]X.H.Dong,K.S.Lau Cauchy transforms of self-similar measures:the Laurent coefficients,[J].Funct.Anal.,2003,202:67 -97.
[2]Hutchinson,J.,Fractals and self-similarity,[J].Indiana Univ.Math.1981,30:713-747.
[3]Falconer K.J.,Fractal Geometry-Mathematical Foundations and Applications[M].New Y ork:John Wiley&Sons,1990,54-65.
[4]肯尼思.法尔科内.分形几何——数学基础及其应用 [M].沈阳:东北大学出版社,1991,65-75.
Abstract:Let the iterated function system(IFS)is of the formSj(z)=εj+ρ(z-εj),whereρis ratio of compression,and 0<ρ<ρm,m≥4,ρmis defined by[1],εj=Kis the attractor of,μis Hausdorff measure of surpport onK.Recently,the paper[1]have studied the Laurent coefficientsof such transformof Hausdorff measure in|z|>1.In this paper,we mainly consider the distributed situation of zero points ofin analytic region.
Key words:zero point; Hausdorff measure; attractor
The Distributed Situation of Zero Points of Certain Cauchy Transforms
LI Hong-guang
(Department of Mathematics,Huaihua University,Huaihua,Hunan 410008)
O174.12
A
1671-9743(2010)05-0020-03
2010-04-07
湖南省教育厅 (06A036)资助项目,怀化学院资助项目.
李红光 (1979-),男,湖南新宁人,怀化学院讲师,硕士,主要研究函数论.
——记嘉荫县红光乡燎原村党支部

