中秋博饼中的数学问题

李艳芳

（福建师范大学 闽南科技学院 理工系，福建 泉州 362332）

中秋博饼中的数学问题

李艳芳

（福建师范大学 闽南科技学院 理工系，福建 泉州 362332）

博饼，是福建厦门三百年来独有的中秋传统活动，是一种独特的月饼文化，也是厦门人对历史的一种传承.相传，中秋博饼，是郑成功屯兵厦门时为解士兵的中秋相思之情、鼓舞士气而发明的.于是，一代一代传下来，就成了如今厦门独具特色的民间习俗.本文从数学的角度，用古典概率和独立性的理论计算各个奖项中奖的概率、哪个奖最难中以及什么奖都拿不到的概率，并分析奖项设置的合理性助.

博饼；古典概率；独立性

1 博饼规则

会饼一套，骰子一副（6个），大瓷碗一个.每个人每次要把6个骰子一起投进大瓷碗里，众人依次投骰子，看骰子点数得饼（奖品）.奖项从大到小如下表所示（关于博饼规则，一秀到对堂是没有争议的；而对于状元里面的分类和大小顺序，各公司、单位及商场在执行的时候略有不同，下表所示是常见的一种规则.规则是人为制定的，制定好后玩家共同遵守，重要的是享受游戏过程中的乐趣）：

?

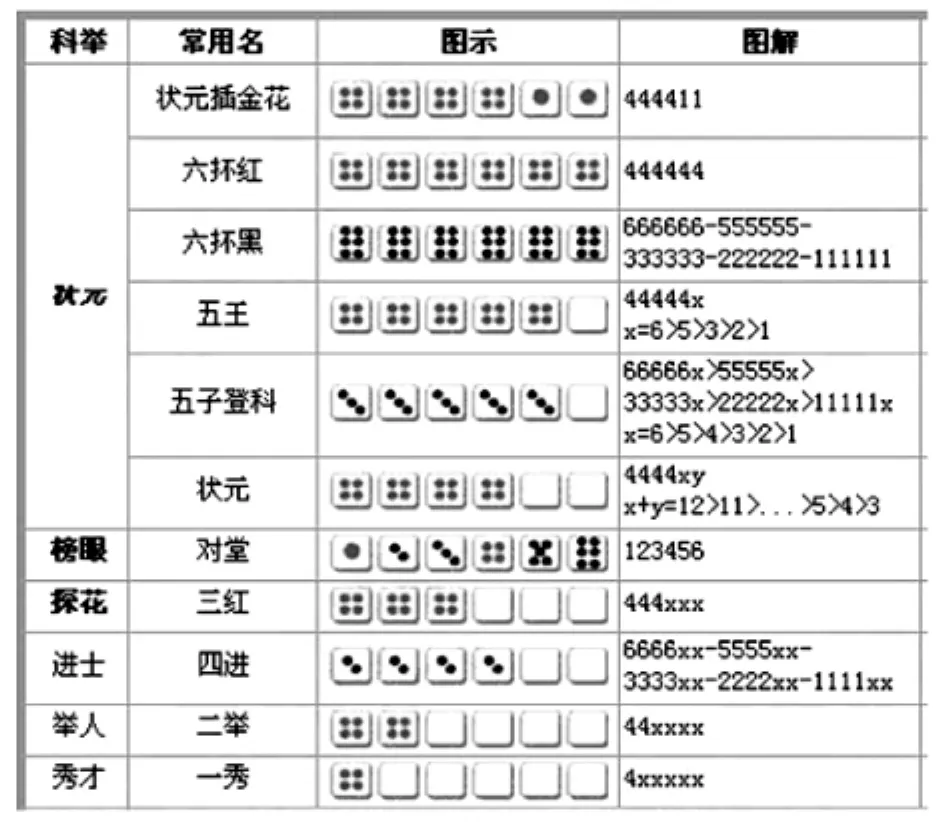
2 奖品设置

一套中秋会饼中，共有大小不同的63块饼.依大小顺序分别为：状元饼1块；榜眼饼2块；探花饼4块；进士饼8块；举人饼16块；秀才饼32块.博饼游戏延续到现代，会饼已经被其他物品所替代，如日用品，食品，购物卷等.这些物品按照会饼规定的数量组合.

3 说明

3.1 如果没有出现上述排列组合中的任何一种情形，则投掷者什么也得不到；如果投掷过程中有骰子溢出瓷碗，则投掷者不仅什么也得不到，下一轮还要轮空；

3.2 如果一个排列组合可以符合多种情形时，按最大者，即按排在表中最上层者算，如两粒红四点，得二举一个，而不能得一秀两个；

3.3 在会饼全部分配完毕前，自第五个三红得主起，后来的三红得主均可以向游戏进行的反方向离自己最近的三红得主追缴三红饼一个；同样，自第三个对堂得主起，后来的对堂得主可以按游戏反方向顺序追缴前面对堂得主的对堂饼一个；

3.4 状元饼的分配，则按大小来算，排在表中上层的为大，如果同时出现五王或五子，则按剩下的那个骰子点数来算，点数大者胜；如果同时出现多人有四粒红四点，则按剩下的2粒骰子的点数之和的大小来算，大者胜；如果点数相同，则先掷出者胜；

3.5 同一博手两次或两次以上博到状元，以最后一次算数，若该博手“禄骨”[同一博手两次博到状元但点数小于先前（先前的状元大于其他博手），也小于其他博手，称为禄骨]，状元即被追缴，若是状元插金花，所得的对堂不被追缴，只追缴状元.

4 概率计算

假设骰子相互独立（相当6个骰子分开摇），得出表中所示骰面组合的理论概率；但实际6骰子一起摇，相互碰撞，独立性假设存在一定误差.

同时掷6只骰子，每一种掷法为一个基本事件，样本空间是由所有可能的骰面组合构成的集合，样本空间中含有66=4665 6个样本点，对于每个骰子而言，每个骰面被掷出的可能性相同，这是一个古典概率问题.表中列出的11种情况两两互不相容.

状元插金花（4个4加2个1）：

p1=C46/66=15/4665 6≈0.0003 2;

六杯红（6个 4）：p2=1/66=1/4665 6≈0.0000 21;

六杯黑（6个都一样，但非6个4）：

p3=5/66=5/4665 6≈0.0001 07;

五王（5个 4，一个非 4）：

p4=C56×6/66=36/4665 6≈0.0007 72;

五子登科（5个一样但不能为4，另外一个与其他 5个不同）：p5=C56×6×5/4665 6=180/4665 6≈0.0038 58;

普通状元（4个4，另外两个均非4，也不能同时为 1）：p6=C46×[5×5-1]/4665 6=360/4665 6≈0.0077 16;

对堂（1到6各一个）：

p7=C16C15C14C13C12C11/66=720/4665 6≈0.0154 32;

三红（3个4，其他3个都非4）：

p8=C36×5×5×5/4665 6=2500/4665 6≈0.0535 84;

四进[4个一样的（非4），另外2个与其他4个不同]:p9=C46×5×5×5/66=1875/4665 6≈0.0401 88;

二举[有2个4，另外4个中不能有4，并且还不能都一样（否则成四进了）]:p10=C26×(5×5×5×5-5)/66=9300/4665 6≈0.1993 31;

一秀[1个4，另外5个的状况有点复杂，其中不能有4，不能都一样（否则成五子登科了），不能有其中4个是一样的（否则成四进了），还不能分别是 1、2、3、5、6（否则就成对堂了）]:p11=C16×(5×5×5×5×5-5-C45×5×4-5!)/4665 6=1749 9/4665 6≈0.3729 42.

5 结果分析

计算结果如表1的左半部分所示.

5.1 六杯红的概率其实是最小的，这个奖项最难获得，从概率的角度把六杯红设置为最高奖更合理；同样如果按照概率小的级别高这样一个原则，对原来的游戏规则进行调整，各奖项从大到小如上表右半部分所示.

表1

5.2 p1+p2+L+p11≈0.6942 73掷一次骰子能得奖的概率为0.6942 73，假设一桌10人，那么一圈之后大概有7人能拿到奖品，全部奖品有63份，理论上9圈后奖品差不多会分完.由于三红和对堂可被追缴，所以实际圈数可能会增加.掷一次骰子什么奖都得不到的概率为0.3057 27，9圈后没有得到任何奖品的概率为 0.3057 279≈0.0000 2，相当于1/5000 0，这个概率非常小，所以基本上大家都能拿到奖品.

5.3 博出状元的概率为p1+p2+p3+p4+p5≈0.0127 96，约1/78，假设一桌10人，理论上，8圈之内应该会出状元.

〔1〕盛骤，谢式千，潘承毅.概率论与数理统计[M].北京：高等教育出版社，2001.

〔2〕陈魁.概率论统计辅导[M].北京：清华大学出版社，2004.

O 21

A

1673-260X（2010）12-0017-02