动态VaR约束下带随机波动的衍生证券最优投资策略＊

2010-10-18 08:27李仲飞李克勉

中山大学学报(社会科学版) 2010年3期

李仲飞,李克勉

其中ε∈(0,1)是给定的VaR风险控制参数。将VaR的表达式(2.15)代入上式,可得投资策略的VaR约束集为:

李仲飞,李克勉

该文研究了连续时间经济下投资者受动态VaR约束时做出的债券、股票和衍生证券最优投资组合策略。金融市场上同时存在股票价格的扩散风险和波动风险,衍生证券的价格不仅依赖于标的股票的价格,还依赖于标的股票的波动,因此借助风险控制的思想对这类风险较大的衍生证券的投资行为进行有效约束是很有必要的。文章通过将随机控制问题转化为确定控制问题得到了该最优化问题的解析解,在理论上借助一些数值例子分析了动态VaR约束如何对衍生证券的投资策略产生影响以及加入这样的风险约束与不进行风险约束相比投资策略发生的变化

随机波动;衍生证券;VaR;风险约束;投资策略

一、引言

本文研究的问题是在连续时间情形下投资者考虑动态(Value-at-Risk,简称VaR)约束时,如何做出债券、股票和衍生证券的最优投资组合决策,以期实现投资者在投资期限结束时财富的期望效用达到最大的目标。本文在莫顿(Merton,1971)经典的连续时间投资组合模型基础上加入以股票为标的的资产的衍生证券,并且假设股票的波动服从均值-回归(Mean-Reverting)的随机过程;同时,投资者还必须动态地受到VaR约束,使得投资者的财富损失程度随时控制在一定的可容忍范围内,这更能反映投资者进行投资风险管理的现实心态。以下是一些文献的回顾。

布莱克和舒尔茨(Black and Scholes,1973)建立的经典欧式期权定价模型是基于一系列假设条件才成立的,其中一条便是假定标的股票的波动率为常数。然而一些文献,如鲁宾斯坦(Rubinstein,1985)、亚克维特和鲁宾斯坦(Jackwerth and Rubinstein,1996)等通过实证研究比较了欧式期权的Black-Scholes理论价格与其市场交易价格的差异,发现标的股票的波动率呈现某种“随机”性质,其隐含波动率随行权价格呈“微笑(Smile)”特征。于是将波动率设定为随机形式进行研究的文献层出不穷,如赫尔和怀特(Hull and White,1987)的对数正态过程,斯科特(Scott,1987)、斯特恩和斯特恩(Stein and Stein,1991)的奥恩斯坦-乌伦贝克(Ornstein-Uhlenbeck,简称OU)过程,以及赫斯顿(Heston,1993)、鲍尔和罗玛(Ball和Roma,1994)的考克斯-英格索尔-罗斯(Cox-Ingersoll-Ross,简称CIR)过程。除对数正态过程外,OU及CIR均为均值-回归过程。因此当标的股票的波动率呈现随机性时,Black-Scholes定价公式便不再成立。

西尔卡和帕帕尼科拉乌(Sircar and Papanicolaou,1999)根据无套利均衡的定价原则,给出了当波动率服从马尔科夫伊藤(Itô)过程时欧式衍生证券的定价形式,该衍生证券的价格同时跟标的股票的价格和波动相关,在到期日的支付(Payoff)根据衍生品种类的不同而不同。刘和潘(Liu and Pan,2003)同时考虑影响金融市场完备性的两个特定因素:随机波动性和价格跳跃性,并以此来研究衍生证券的投资策略问题。该文借鉴Heston(1993)的随机波动率模型,又将跳跃风险加入股票价格的运动方程,进而使得衍生证券的价格过程被假定受股票价格、波动率和跳跃性三者的影响。该文在效用函数采用CRRA(Constant Relative Risk Aversion)型,目标为最大化终端财富期望效用的情形下,通过随机控制方法求得最优投资组合策略的解析表达式。何苏库(Hsuku,2007)在Liu和Pan(2003)的基础上研究跨期消费和衍生证券投资问题,不过只考虑了随机波动性这一个因素。该文采用达菲和爱泼斯坦(Duffie and Epstein,1992)提出的连续时间递归偏好(Continuous Time Recursive Preference)效用形式,给出跨期替代弹性为1时的消费及衍生证券投资最优策略解析式以及不为1时的近似表达式。

VaR是近年来度量和控制金融风险最常用的工具之一。具体来说,VaR是指在一段时间内,在给定置信水平下,财富损失可能达到的最大数额。对于连续时间情形的投资组合决策问题,如何动态地将财富可能的最大损失控制在给定范围内,以下文献给出了一些理论研究。库欧科、何和爱沙恩库(Cuoco,He and Isaenko,2007)在经典的Merton(1971)框架下加入VaR约束,假定一段很小的时间间隔内市场参数及投资头寸不发生变化,投资者在这段间隔内财富的VaR数额被限定在一定范围内。由于投资期连续地由这些很小的时间间隔组成,因此投资者在投资期内能反复度量投资组合的风险,财富的数额连续地受到风险约束,进而在这更加现实的动态一致性模型下实现最优投资策略的选择。皮尔乌(Pirvu,2007)采用与上述文献相同的假设,同时考虑消费和投资的最优选择。与之不同的是,前者运用随机控制方法求解,后者的求解方法主要是利用Itô积分的鞅性质将该随机控制问题转化为确定控制问题。该文在最大化跨期消费及终端财富的总效用目标下给出自然对数效用形式下最优策略的解析解和一般CRRA效用形式下的数值解。陈、李和李(Chen,Li and Li,2009)也采用同样的VaR约束方法研究保险公司的投资和再保险策略,目标是最小化保险公司的破产概率,并得到最优策略的解析解。

本文在前述文献的基础上所做的研究是,在衍生证券的投资过程中动态地加入风险控制,以便有效地随时约束风险性较大的衍生品投资。Liu和Pan(2003)及Hsuku(2007)设定的衍生证券同时考虑了标的资产价格的扩散风险和波动风险,但它们对风险如此大的衍生品投资的分析却没有考虑到投资过程中投资者财富可能出现巨大损失的可能性。本文在此基础上采用Cuoco,He和Isaneko(2007)的思想,在连续时间的投资过程中动态地加入VaR约束。假设在某个很小的时间区间内市场参数及投资策略不发生变化,并用VaR度量这个间隔内财富损失的风险。倘若每一个给定的时间区间内都这样度量财富损失的风险,那么财富将会连续地满足风险约束的要求。借鉴Pirvu(2007)的求解方法,通过将随机控制问题转化为确定控制问题,本文给出该最优化问题的解析解,即得到了在加入动态VaR约束后投资股票和衍生证券的最优策略。从这个最优策略的表达式可以看出,进行风险约束后投资者将会更加谨慎地进行投资决策:越严格地控制财富损失的风险,就会越小比例地投资风险资产(包括股票和衍生证券)。另外一个有趣的结论是,本文给出的最优投资行为既可以选择与未考虑风险控制的情形同向的操作,也可以选择与之反向的操作,只是要求进行同向或反向的操作时两个风险资产同时都要进行。

二、模型的建立与描述

(一)金融市场环境

本文考虑连续时间情形下的随机经济,数学模型的随机性建立在概率空间(Ω,F,P)上。假设金融市场上存在债券和股票这两种基础证券,以及一种以股票为标的资产的衍生证券。

债券是无风险资产,价格过程如下:

其中利率r>0为常数。

股票是风险资产,代表整个股权市场,价格服从下面的动态过程:

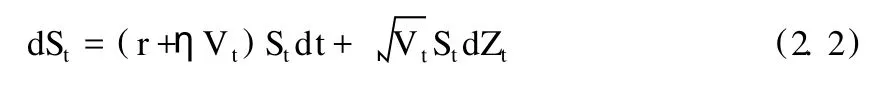
其中Zt是标准布朗运动,反映股价的扩散风险。这里假定股票的预期超额收益ηVt随其波动Vt的变动而变动①严格意义上来说,t表示股票收益的波动率,Vt表示股票收益的方差。,常数η反映这种变动的程度,即股票收益的风险溢价程度。波动则参照Heston(1993)的假设,服从下面的均值-回归过程:

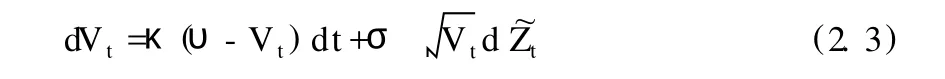
其中κ>0表示均值-回归的规模,υ>0表示波动收敛的长期均值,σ≥0表示波动的系数;~Zt也是标准布朗运动,是市场上除了扩散风险外的另一风险源,它反映的是股票的波动风险。假设这两种风险源的相关系数为常数ρ∈(-1,1),则d一般地,假设ρ<0。直观上看,波动风险越大,波动得越频繁越激烈,资产的价格就会越低。可将~Zt分解为两部分,如下所示:

衍生证券以上述股票为标的资产,其价格形式采用Liu和Pan(2003)及Hsuku(2007)的设定。具体来说,衍生证券价格是标的股票的价格及其波动的函数,运动方程如下:

其中常数ξ反映随机波动的风险溢价程度②股票价格的波动风险表示为Z~t,严格来说,ξ反映的是风险源Z¯t的溢价程度。。这里gS和gV分别衡量股票的价格和波动发生变化时衍生证券价格的变化程度,具体形式如下:

非零的gS和gV反映衍生证券对扩散风险和波动风险的暴露(Exposure)。

对此衍生证券的价格过程需要说明以下三点:首先,这是根据无套利均衡定价原则给出的一般形式,具体的衍生品种类由其到期日具体的支付形式来确定。比如g(τ,Sτ,Vτ)=max(Sτ-K,0)表示该衍生品为欧式看涨期权,g(τ,Sτ,Vτ)=max(K-Sτ,0)表示其为欧式看跌期权,其中τ和K分别表示上述期权的到期日和行权价格。其次,该衍生证券的到期时间不一定要与投资者的投资期限一致,只要在投资期限内存在这样的衍生品就行。比如一个投资者做10年的证券投资决策,他选择投资的期权也许在两年内就到期。但只要该期权到期后市场上仍存在具有相同价格过程(2.6)的与之相同或不同种类的衍生品,他就可以继续投资该新的衍生品。因此他只需关注在投资的时刻如何选择衍生品的投资,而不需考虑其到期后的情况。第三,只要ρ≠±1,该衍生品就能使市场完备,是非冗余的证券。任意由风险源Z和所驱动的风险资产,其支付都可由股票和该衍生证券的支付的组合复制出来。因此,它能完备地反映出市场上存在的两种基本风险:扩散风险和波动风险。

(二)交易策略及财富过程

本文讨论投资者采取自融资方式进行投资操作行为,即他的财富变化源自于投资损益,没有额外的资金注入或撤出;同时假设市场允许投资者卖空,即证券的头寸可以为负;另外,头寸的再调整不产生任何交易费用。

令Wt表示投资者在时刻t拥有的财富,他所做的决策是确定在时刻t投资于股票及衍生证券上的财富比例θt和φt。自然地,投资在债券上的财富数额即为(1-θt-φt)Wt。于是他的财富满足下面的动态过程:

合理地假设:

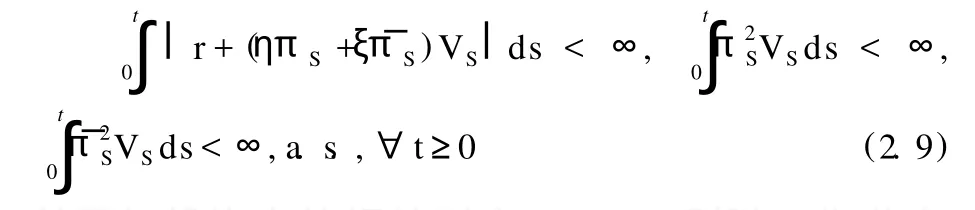
并已知投资者的初始财富W0>0,则随机微分方程(2.7)存在惟一解:

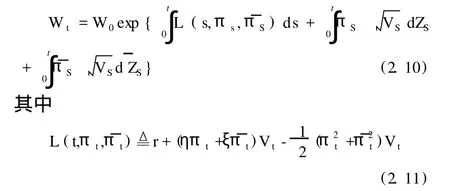
(三)动态VaR约束

本文依据Cuoco,He和Isaenko(2007)的方法计算投资者财富损失的VaR数额。考虑从某个时刻t≥0开始,固定一个很小的时间间隔δ>0。假设在时间区间[t,t+δ]内市场参数以及交易策略均不发生变化,则投资者在时刻t+δ的财富为:

进而在[t,t+δ]内财富的损失额为:

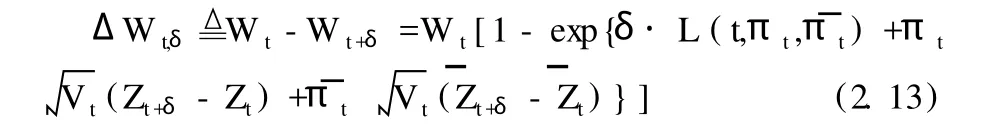
给定置信水平为1-α,α∈(0,1/2]。根据VaR的定义,投资者在[t,t+δ]内财富损失的VaR数额满足:

令Φ(·)表示标准正态累积分布函数,Φ-1(·)为其反函数,则VaR的表达式由命题2.1给出。

命题2.1 给定1-α的置信水平条件下,投资者在[t,t+δ]内财富损失的VaR水平为:

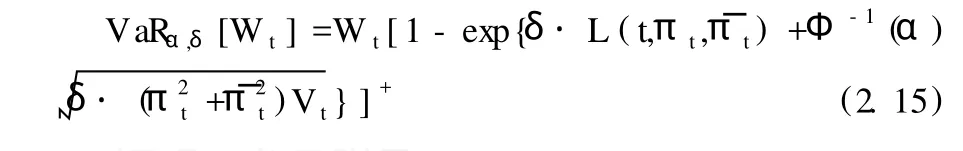
证明参见附录1。

本文借鉴Pirvu(2007)的思想,考虑财富损失率的概念,即财富损失的VaR数额与财富数额的比例。于是在连续时间投资组合选择问题中加入的风险约束即为财富损失率在每个交易时刻不超过事先给定的水平。具体来说,VaR约束表示为投资者在任一时刻t所做的投资决策(θt,φt)或必须满足:

其中ε∈(0,1)是给定的VaR风险控制参数。将VaR的表达式(2.15)代入上式,可得投资策略的VaR约束集为:

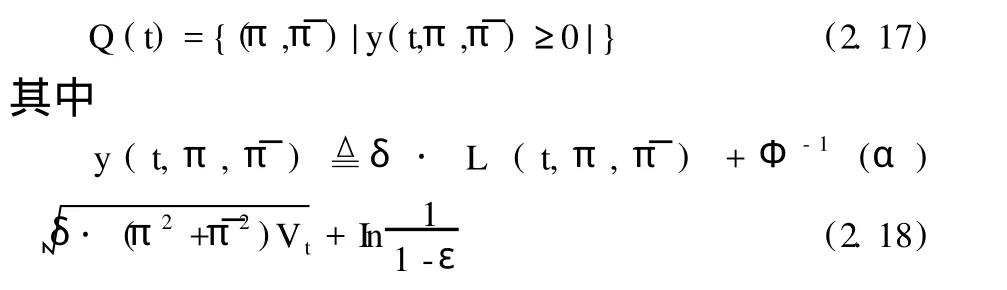
(四)投资者追求的目标

假设投资者从初始时刻开始参与金融市场的投资活动,投资期为给定的T>0。他的行为是在时期[0,T]内的每一时刻做出债券、股票以及衍生证券的投资决策,同时在每一时刻控制较小的财富损失率,目标是最终实现终端时刻财富期望效用的最大化。

本文采用自然对数型效用函数U(x)=Inx来衡量风险规避投资者的财富效用。由于本文主要考察的是衍生证券的最优投资策略在加入动态风险约束后,相较不控制风险的情形将会发生何种变化,因而效用函数形式没有考虑风险厌恶参数的作用和影响。于是投资者面临的最优投资策略问题如下:

这是一个受两个状态过程(2.5)和(2.7)约束的随机控制问题。常用的求解方法是构建Hamilton-Jacobi-Bellman(简称HJB)方程,猜测值函数的形式,运用随机动态规划知识得到控制变量和状态变量的最优路径。在本文中,由于控制变量(即证券投资决策)还受到VaR约束集的影响,求解上述高阶非线性偏微分方程比较困难,因此本文采用Pirvu(2007)中将随机控制问题转化为确定控制问题的手段求解最优化问题(2.19)。第三节便利用这种方法求得该问题的最优解析解。

三、最优投资组合策略

考虑投资者的财富方程(2.10),对其两端取自然对数,得:

假设股票的随机波动Vt满足:

这是一个技术性假设,但对于一般的金融市场而言,这个假设也是合理的。

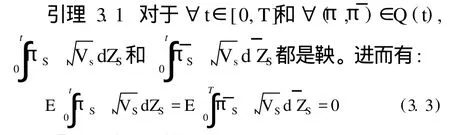
证明参见附录2。

由引理3.1的结论可知,投资者终端时刻财富的期望效用为:

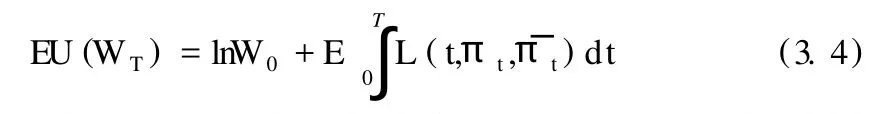
引理3.2 对任意给定的路径ω∈Ω和时刻t∈[0,T],如果是函数的最大值点,即:

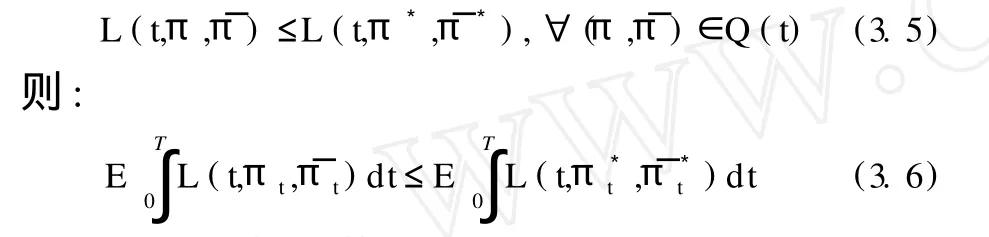
证明参见附录3。

根据引理3.2的结论并结合(3.4)可知,在动态风险约束下,若要最大化EU(WT),可以先同时固定路径ω∈Ω和时刻t∈[0,T],选择最优的(π,¯π)∈Q(t)来最大化L(t,π,¯π)。于是原动态最优化问题(2.19)可先转化为如下静态最优化问题的求解:

引理3.3 对任意给定的路径ω∈Ω和时刻t∈[0,T],最优化问题(3.7)的解为:

证明参见附录4。

定理3.4 在动态VaR约束下,投资者为实现其终端财富期望效用最大化的目标而选择的股票和衍生证券的最优投资组合策略如下:令

证明参见附录5。

至此,本文已经给出在动态VaR约束下股票和衍生证券的最优投资策略。定理3.4表明,不加入风险控制而直接进行投资操作所得的最优策略即为情形1°的结果(3.10);进行了动态VaR约束后最优投资策略则要根据市场参数以及VaR约束带来的外生参数所满足的条件来确定,即为情形2°的结果(3.11)。下一节将研究市场参数(如随机波动Vt等)和外生参数(如置信水平1-α等)对最优投资组合策略选择的影响,以及动态VaR约束对投资策略产生的影响和作用。

四、最优策略的经济分析

(一)最优投资组合策略的选择

与Liu和Pan(2003)不考虑股票价格跳跃的情形及Hsuku(2007)最大的不同之处在于,本文引入动态VaR约束后最优证券投资组合策略将直接受到来自由VaR约束带来的外生参数1-α,δ和ε,即置信水平、时间间隔和风险控制参数的影响。由定理3.4可知,两种不同情形下最优策略的选择是不同的。市场参数中的随机波动Vt,股票收益和随机波动的风险溢价程度η和ξ,无风险利率r,再加上前述三个外生参数一起,共同决定了最优策略的选择。

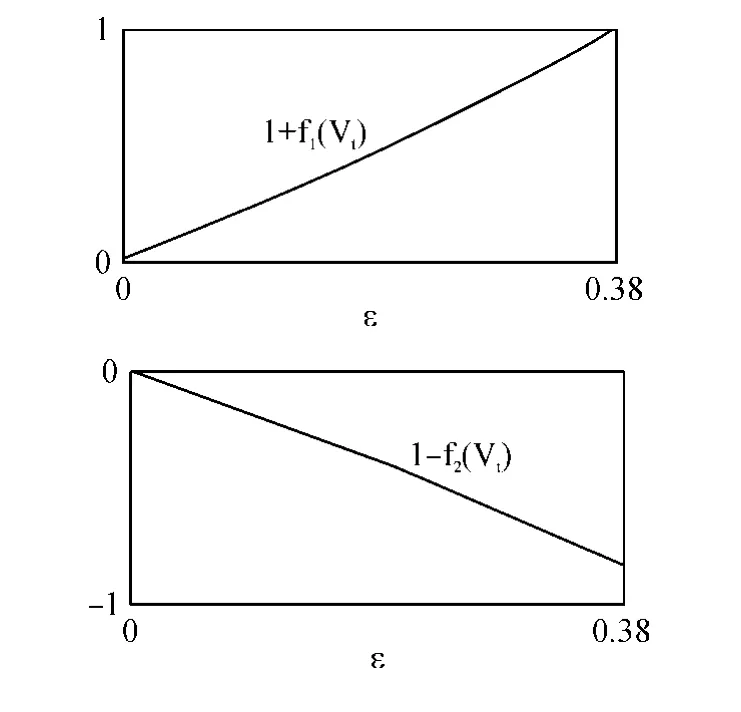
当r,α,δ和ε满足Δ>0条件时,则需依据随机波动Vt的取值来确定的表达式。若最优策略仍由(3.10)给出,具体的经济分析如前所述,此处不再赘述。若则最优策略由(3.11)给出,这是定理3.4中的情形2°。这时,本文发现以下四个有趣的结论。第一,(3.11)给出的最优策略有两个,投资者不论选择哪一个,都能实现终端财富期望效用最大化的目标。第二,情形2°下的股票及衍生证券投资策略都与情形1°呈正比例关系,比例系数要么同为1+f1(Vt),要么同为1-f2(Vt)。第三,由f1(Vt)和f2(Vt)的表达式(3.9)可以看出,1+f1(Vt)>0,1-f2(Vt)<0。这说明情形2°下的投资操作与情形1°相比,既可让两种风险资产同时与之同向操作,亦可让两者同时与之反向操作。例如0表明情形1°下投资者在时刻t持有股票和卖空衍生证券,倘若参数的值满足情形2°,那么投资者在时刻t可以选择持有财富比例的股票和卖空|财富比例的衍生证券,也可以选择卖空财富比例的股票和持有财富比例的衍生证券。第四,根据情形2°下参数所满足的条件可推得这个结论由以下命题给出。

命题4.1 当定理3.4中的情形2°出现,即Δ>0且N1

证明参见附录6。

由此可知,情形2°相较情形1°而言,两种风险资产的投资组合策略在绝对值意义上来说是同比例减少了。仍以前述情形1°下<0为例,在情形2°时,若两者同时采取与情形1°同向的操作,则投资者在时刻t持有的股票份额将比情形1°时同比例的少,而卖空的衍生证券份额也将同比例的少;若两者同时采取与情形1°反向的操作,则投资者在时刻t选择卖空股票和持有衍生证券,但卖空的股票份额却比情形1°时持有的股票份额同比例的少,持有的衍生证券份额也比情形1°时卖空的衍生证券份额同比例的少。

(二)财富损失率的约束对投资策略的影响

由对投资者财富的动态VaR约束所带来的三个外生参数中,置信水平1-α和时间间隔δ可根据现实的金融市场环境来确定。例如,1995年4月巴塞尔银行监督管理委员会在对银行资本充足率进行风险管理时,要求各银行计算的VaR数额需基于10个交易日(或两个星期)和99%的置信水平①参见乔瑞(Jorion,2001)第3章第3节的描述。。因此本文着重研究风险控制参数ε(即财富损失率的约束)如何影响投资者的投资行为。一般来说,ε越小表明投资者对财富的损失情况控制得越严格,即是对投资风险的厌恶程度越高。

参照Liu和Pan(2003)对市场参数的设定,本文取无风险的年利率r=5%,股价的风险溢价程度η=4,波动的风险溢价程度ξ=-6,股票在时刻t的瞬时波动率根据前述巴塞尔委员会在要求各银行计算VaR时对各参数的设定,本文取置信水平1-α=99%(即Φ-1(α)=-2.326),时间间隔δ=0.04②假设全年共有250个交易日,则10个交易日即为0.04年。。由于本文着重研究在加入VaR约束后的投资策略所发生的变化,且Liu和Pan(2003)及Hsuku(2007)已经研究了各市场参数对未加风险约束情形的股票及衍生证券投资策略的影响,因此本文的数值例子仅分析情形2°中正比例系数随变化而产生的变化。由前面H(r,η,ξ,Vt;α,δ)的表达式可算出H≈38%,这表明若财富损失率控制在38%以内,投资者将采取(3.11)给出的投资操作行为。此时,结合f1(Vt)和f2(Vt)的表达式(3.9)可描绘出正比例系数与ε的关系,如图1所示。

图1 正比例系数与风险控制参数ε的关系

上图显示情形2°下两种风险资产同时采取与情形1°同向操作时正比例系数随ε严格递增,下图显示反向操作时正比例系数随ε严格递减。

五、结论

本文研究了连续时间经济下投资者受动态VaR约束时在债券、股票和衍生证券市场上做出的最优投资组合决策。市场上同时存在股票价格的扩散风险和波动风险,衍生证券为了同时对冲这两种风险并使市场完备而被设计出来。然而投资这样的衍生品本身就具有很大的风险,因此随时约束此类衍生品投资是很有必要的。本文的结论表明,考虑了财富损失的风险约束后,投资者将会更加谨慎地进行财富的投资分配。对股票和衍生证券这样的风险资产,投资者将会做出与没有考虑任何风险约束的情形相同或者规模更小的投资操作行为;自然地,投资者将更加垂青债券这样的无风险资产。

不过,仍有一些问题可作思考。第一,本文考虑了市场上的两种风险,但倘若存在其他的风险源(比如股票价格的跳跃风险),有更多对冲这类风险的衍生证券出现,那么投资者应如何约束或控制此种风险更大的衍生品投资呢?第二,本文采用VaR方法来度量投资的风险,但阿次恩尔等(Artzner et al.,1999)指出,VaR不满足次可加性因而并非一致的风险测度,而且它不能度量财富损失的尾部风险,以至于有可能在极小的概率出现时发生巨大的财富损失。那么使用其他的风险测度是否会有更好的效果呢?比如Conditional Value-at-Risk(简称CVaR)或称为Conditional Tail Expectation(简称CTE)风险测度。CVaR或CTE被定义为一段时间内给定置信水平条件下财富损失超过其VaR数额的条件期望值,它克服了VaR的上述两大缺陷。用CVaR代替VaR进行动态的风险约束能否使投资组合策略更好地服务于投资者追求的目标?第三,本文采用的效用函数是最简单的自然对数型,它是CRRA型当相对风险厌恶参数等于1时的特例。倘若使用更一般的CRRA型来衡量投资者财富的效用是否会对最优投资组合策略带来某些影响或变化?以上问题将作为作者进一步研究的方向。

Artzner,P.,Delbaen,F.,Eber,J.and Heath,D.,1999.Coherent measures of risk,Mathematical Finance,Vol.9,203-228.

Ball,C.A.and Roma,A.,1994.Stochastic volatility option pricing,Journal of Financial and Quantitative Analysis,Vol.29,589-607.

Black,F.and Scholes,M.,1973.The pricing of options and corporate liabilities,Journal of Political Economy,Vol.81,637-654.

Chen,S.,Li,Z.andLi,K.,2009.Optimal investment-reinsurance policy for an insurance company with VaR constraint,Working Paper.

Cuoco,D.,He,H.and Isaenko,S.,2007.Optimal dynamic trading strategies with risk l imits,Operations Research,Articles in Advance,1-11.

Duffie,D.and Epstein,L.G.,1992.Stochastic differential utility,Econometrica,Vol.60,353-394.

Heston,S.L.,1993.A closed-form solution foroptionswith stochastic volatilitywith applications to bond and currency options,Review of Financial Studies,Vol.6,327-343.

Hsuku,Y.,2007.Dynamic consumption and asset allocation with derivative securities,Quantitative Finance,Vol.7,137-149.

Hull,J.andWhite,A.,1987.The pricing of options on assetswith stochastic volatilities,Journal of Finance,Vol.42,281-300.

Jackwerth,J.C.and Rubinstein,M.,1996.Recovering probabilitydistributionsfromcontemporaneoussecurity prices,Journal of Finance,Vol.51,1611-1631.

Jorion,P.,2001.Value at Risk:the new benchmark for managing financial risk,McGraw-Hill,New York.

Liu,J.and Pan,J.,2003.Dynamic derivative strategies,Journal of Financial Economics,Vol.69,401-430.

Merton,R.C.,1971.Optimum consumption and portfolio rules in a continuous-time model,Journal of Economic Theory,Vol.3,373-413.

Pirvu,T.A.,2007.Portfolio optimization under the Valueat-Risk constraint,Quantitative Finance,Vol.7,125-136.Rubinstein,M.,1985.Nonparametric tests of alternative option pricingmodels using all reported trades and quoteson the 30 most active CBOE option classes from August 23,1976 through August 31,1978,Journal of Finance,Vol.40,455-480.

Scott,L.O.,1987.Option pricingwhen the variance changes randomly:Theory,estimation,and an application,Journal of Financial and Quantitative Analysis,Vol.22,419-438.

Sircar,K.R.and Papanicolaou,G.C.,1999.Stochastic volatility,smile&asymptotics,Applied Mathematical Finance,Vol.6,107-145.

Stein,E.M.and Stein,J.C.,1991.Stock price distributionswith stochastic volatility:an analytic approach,Review of Financial Studies,Vol.4,727-752.

附录

1. 命题2.1的证明

因为ΔWt,δ是连续型随机变量,所以(2.14)等价于