内积空间上向量值 Padé-型逼近表的块状结构特征

苏 瑞, 潘宝珍

(上海大学 理学院,上海 200444)

内积空间上向量值 Padé-型逼近表的块状结构特征

苏 瑞, 潘宝珍

(上海大学 理学院,上海 200444)

从多项式空间到向量空间引入一种广义线性泛函,在内积空间上定义和构造向量值 Padé-型逼近.借助向量值 Padé-型逼近的误差公式,给出关于线性泛函的正交多项式的定义,同时推导出向量值 Padé-型逼近表的块状结构特征.利用 Padé-型逼近表的这一特征,可以减少向量值 Padé-型逼近的计算量.最后,通过数值实例说明该方法的有效性.

向量值;Padé-型逼近;正交多项式;块状结构特征

Abstract:A vector-valued Padé-type approximation is defined in the inner space by introducing a generalized linear functional from a polynomial space to a vector space.With the error formula for vectorvalued Padé-type app roximation,the orthogonal polynomial w ith respect to a generalized linear functional is defined.The block structure of Padé-type table is derived. The structure can be used to reduce computation of Padé-type approximations.An example is given to illustrate effectivenessof themethod.

Key words:vector-valued;Padé-type approximation;orthogonal polynomial;block structure

Padé-型逼近在理论物理、系统控制理论、模型简化和积分方程领域都有着广泛的应用.从 1979年法国数学家 Brezinski[1]研究了数量 Padé-型逼近开始,许多数学工作者将 Padé-型逼近理论加以发展.1983年,Draux[2]将 Padé-型逼近从数量情形推广到非交换代数的情形,并提出矩阵 Padé-型逼近.1999年,Salam[3]将 Padé-型逼近推广到向量情形,向量值Padé-型逼近是借助于 Clifford代数的方法来定义,该方法在具体计算中很难实现.2004年,顾传青[4]引入一种从多项式空间到矩阵空间上的广义线性泛函,从而在矩阵内积的基础上构造和定义了矩阵值Padé-型逼近.

本研究借助于向量值 Padé-型逼近的误差公式及高阶向量值 Padé-型逼近[5-7],推导出向量值 Padé-型逼近表的块状结构特征,即当向量值 Padé-型逼近的生成多项式取为关于线性泛函的正交多项式时,块状结构特征表中的逼近元素及逼近阶是完全相同的,可以利用该特征在计算高阶向量值 Padé-型逼近时减少计算量.

1 向量值 Padé-型逼近的定义与构造

向量 a=(a1,a2,…,ad)∈Cd,b=(b1,b2,…,bd)∈Cd,ai,bi∈C.它们的内积定义为

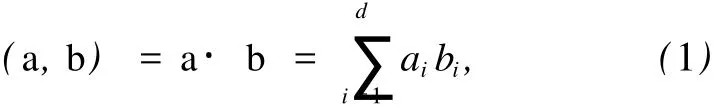
定义向量 g=(g1,g2,…,gd)∈Cd的范数

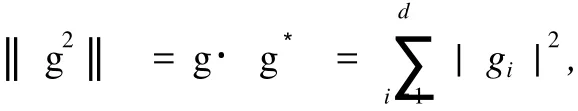
这里 g＊表示 g的复共轭.

向量 g的广义逆 (Samelson逆)定义为

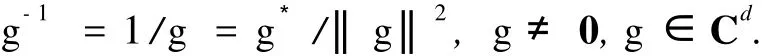
设 P是一元实系数多项式,Pk表示 P中次数不超过 k的多项式的集合.设向量 g形式幂级数为

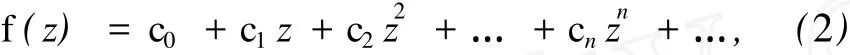
式中 ,ci∈Cd,z∈C.

设 φ:P→Cd为作用在多项式空间到向量空间上的线性泛函,定义为

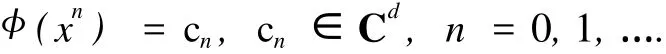
如果 |xz|<1,则有 (1-xz)-1=1+xz+(xz)2+….将线性泛函作用在 (1-xz)-1上,可得

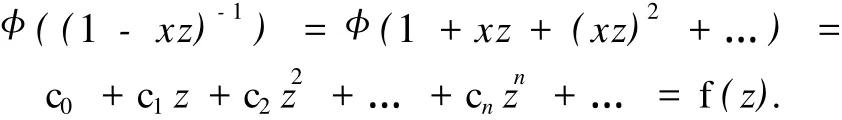
设 v∈Pn是次数为 n的数量多项式,有

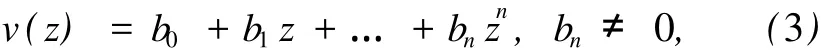
定义具有向量值系数的多项式W(z)为

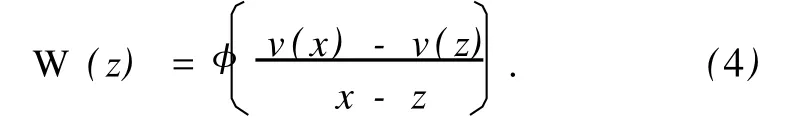
注意到 φ是作用于多项式空间的广义线性泛函,因而W(z)是关于 z的次数为 n-1的具有向量值系数的多项式.再令

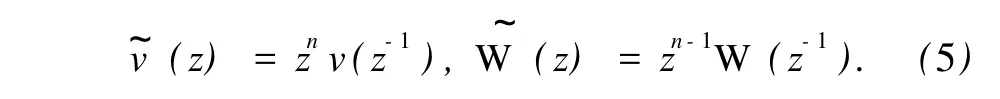
定理1[5]设v～(0)≠0,则成立

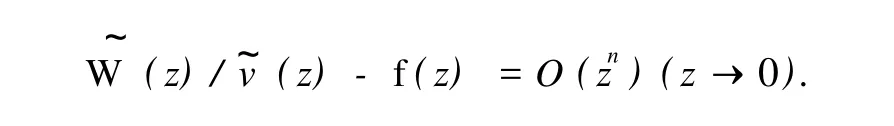
设 φ(l):P→Cd是作用于多项式空间到向量空间的广义线性泛函,定义为

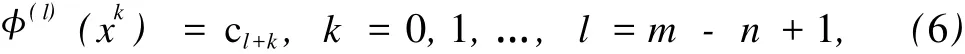
当 l+k<0时 ,规定 φ(l)(xk)=0.

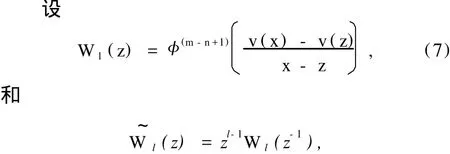
根据构造公式 (4)～(7),定义

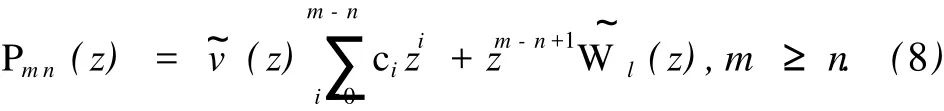
定理2[5]设v～(0)≠0,则成立Pmn(z)/

定义 2 定义向量值函数 Rm,n(z)=Pmn(z)/为(m,n)阶向量值Padé-型逼近,记为(m/n)f(z).

2 向量值 Padé-型逼近表的结构特征

由向量值 Padé-型逼近误差公式[5],有

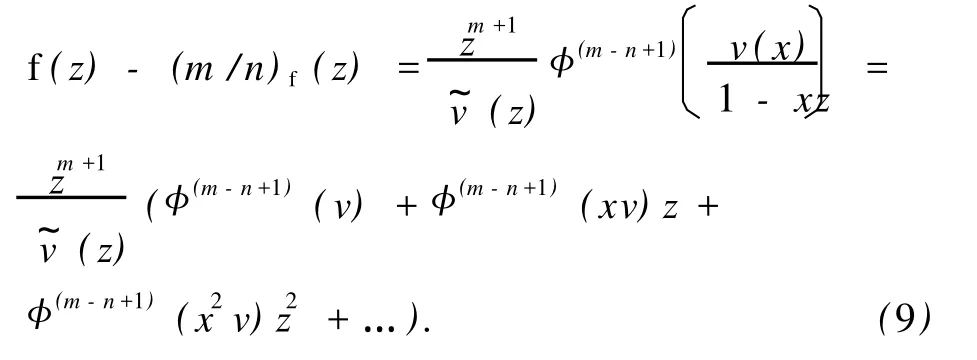
根据 (m/n)f(z)的构造方式可知,(m/n)f(z)实际上取决于 n个任意常数,为此令

定义 3 满足方程 (10)的数量多项式 v(x)定义为关于广义线性泛函 φ(m-n+1)的正交多项式,由正交多项式 v(x)所确定的 (m/n)f(z),称为给定向量幂级数 f(z)的高阶向量 Padé-型逼近.

若在式 (10)中代入 v(z)=b0+b1z+…+bnzn,施加广义线性泛函 φ(m-n+1),并与向量 cm-n+1分别作内积,得到下列线性方程组:

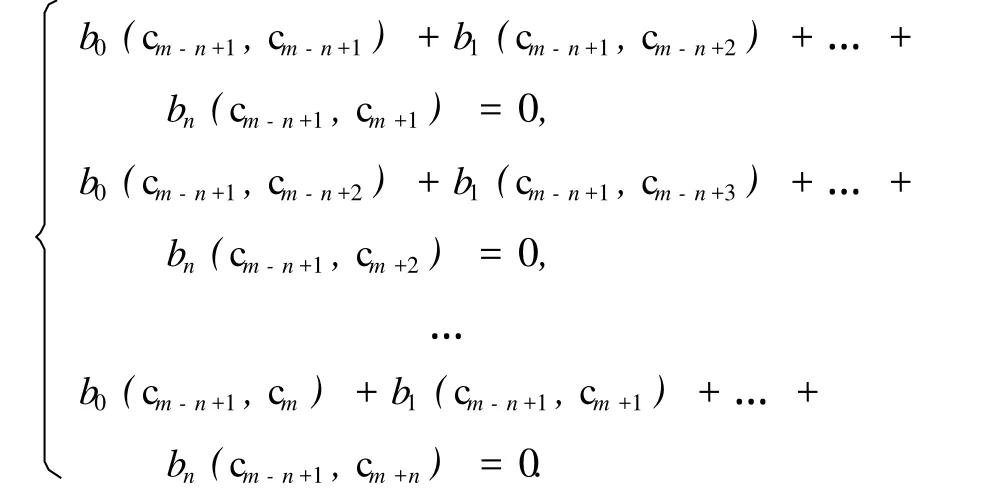
通过上述方程组已完整建立向量值 Padé-型逼近的行列式表达式[5].本研究在此基础上讨论由正交关系 (10)确定的生成多项式所构造的向量值Padé-型逼近表的分布特征.

定理 3 设 (1)vn(x)满足

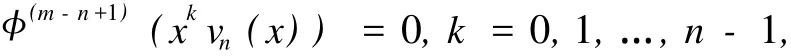
而 up(z)是任一关于 z的 p次多项式 (0≤p≤n);(2)(m/n)f(z)是 f(z)的以 vn(z)为生成多项式的向量 Padé-型逼近,则向量幂级数 f(z)的以 v(z)=up(z)vn(z)为生成多项式的 (m+p+h/n+p)f(z)向量值 Padé-型逼近满足

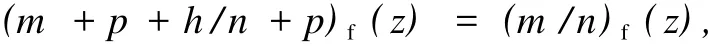
式中,0≤p+h≤n.

证明 由高阶向量值 Padé-型逼近的定义得

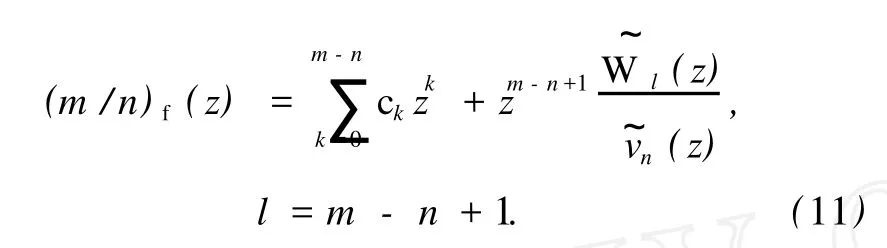
将式中 m换为 m+p+h,n换为 n+p,以 vn(z)up(z)为生成多项式,构造的向量值 Padé-型逼近,有

由式 (14),可推出

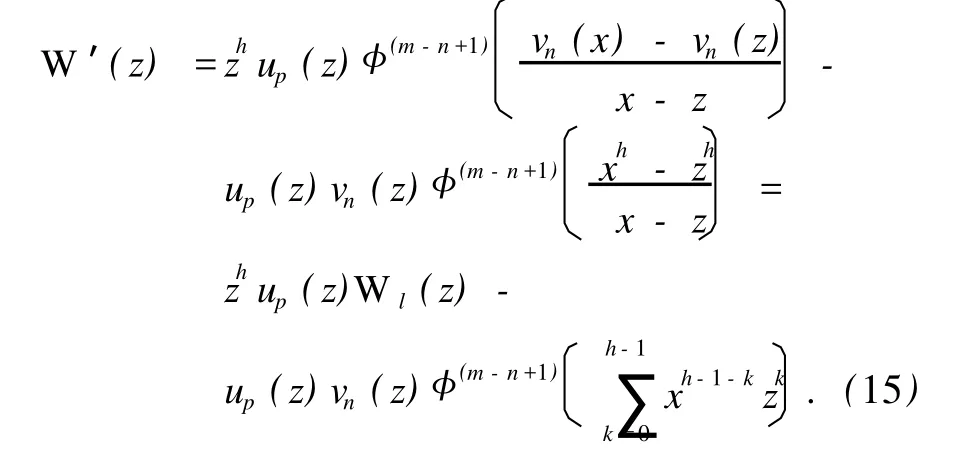
注意到泛函只作用在 x上,观察式 (13)发现,W′(z)实际上是关于 z的 n+p-1次多项式,即

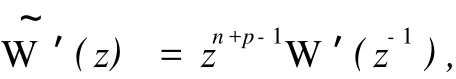
于是,有

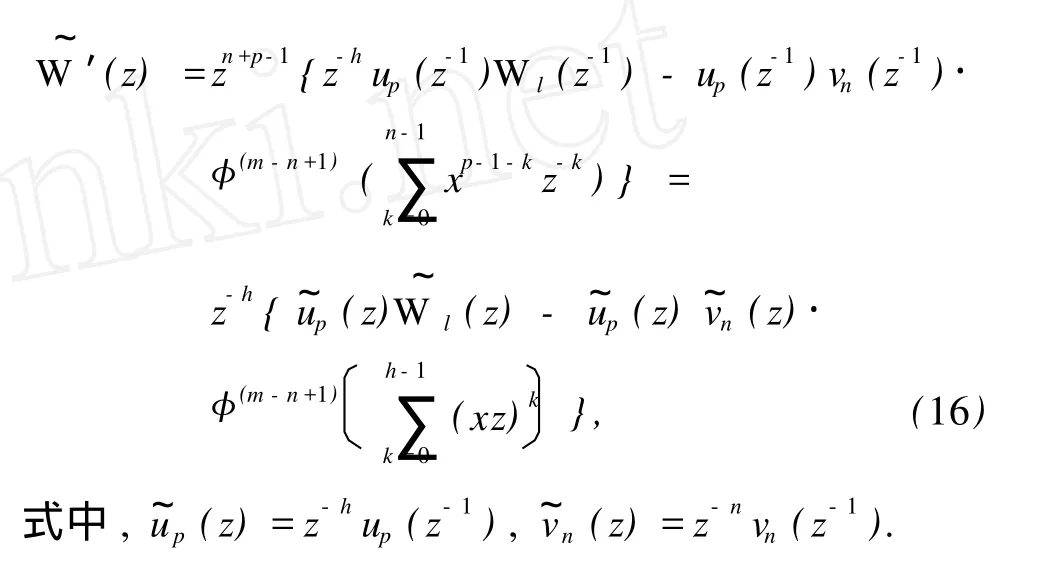
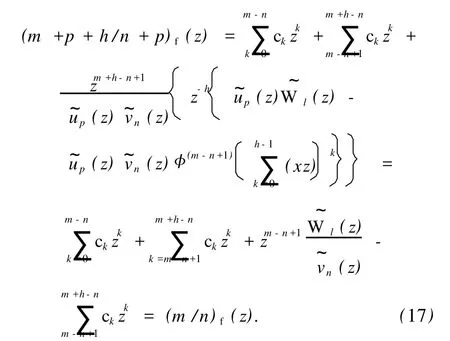
注解 1 只有在给定生成多项式且此生成多项式是有正交关系确定的条件下,定理 3成立.

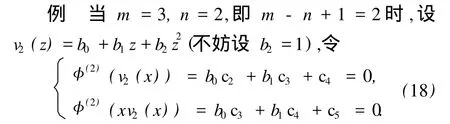
对方程组 (18)中的每一个方程分别与向量 c2作内积,所求得的形式正交多项式为 v2(z).记 (3/2)f(z)是以 v2(z)为生成多项式的 Padé-型逼近 ,则由定理 3得

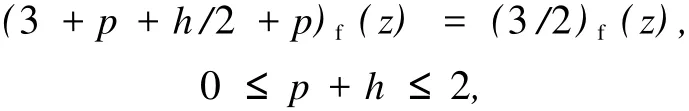
式中,(3+p+h/2+p)f(z)是以 up(z)v2(z)为生成多项式的 Padé-型逼近,up(z)是任意 p次多项式 (0≤p≤2).如此得到向量值 Padé-型逼近表块状结构特征,即如下的逼近元素相同(逼近阶也完全相同):

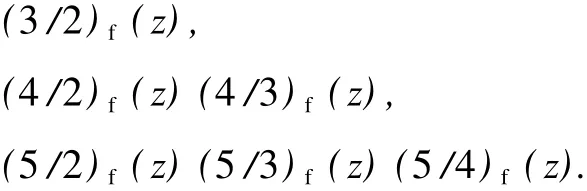
注解 2 若要计算 (5/4)f(z),根据注解 1,只要计算 (3/2)f(z).这样减少了向量值 Padé-型逼近的计算量,但逼近阶却达到 O(z6).

例 1 考察控制论中的向量指数函数

解 当把向量值 Padé-型逼近 (5/4)f(z)的生成多项式取为正交多项式v～2(z)时,根据定理2,只需计算 (3/2)f(z),其分子、分母分别计算[5]如下:易验证(3/2)f(z)=(5/4)f(z)=P32(z)/v～2(z).

[1] BREZINSKI C. Padé-type approximation and general orthogonal polynomials[M].Basel:Birkhäuser,1980.

[2] DRAUX A.Approximants de type Padéet de Padé[M].Lille:Universiédes Science et Technologies de Lille,1983:1-89.

[3] SALAM A.Vector Padé-type approximants and vector PadéApp roximants[J].JApp roximation Theory,1999,97(1):92-112.

[4] GU C Q.Matrix Padé-type approximant and directional matrix in the inner p roduct space[J].J Comput Appl Math,2004,164/165:365-385.

[5] L IC J.A new vector-valued Padé-type approximation in the inner space[J].Numer Math J Chinese Univ:English Series,2006,15(2):127-136.

[6] 潘宝珍.用于积分方程解的函数值 Padé-型逼近的恒等式与递推算法 [J].应用科学学报,2006,24(1):74-77.

[7] GU CQ,PAN B Z,WU B B.Orthogonal polynomials and determinant formulas of function-valued Padé-type approximation using for solution of integral equations[J].Appl Math Mech:Engl Ed,2006,27(6):853-860.

(编辑:孟庆勋)

Block Structure of Vector-Valued Padé-Type Table in the Inner Space

SU Rui, PAN Bao-zhen
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

O 241.83

A

1007-2861(2010)03-0253-04

10.3969/j.issn.1007-2861.2010.03.007

2008-12-05

上海市重点学科建设资助项目 (J50101)

潘宝珍 (1965～),女,副教授,博士,研究方向为泛函分析.E-mail:bzpan@staff.shu.edu.cn