式与方程

■齐昌建

式与方程

■齐昌建

复习要求

1.进一步掌握用字母表示学过的运算定律和计算公式，能够在具体的情境中用字母表示常见的数量关系，会根据字母所取的值，求含有字母式子的值。

2.进一步理解方程.方程的解.解方程的意义以及等式的基本性质，掌握简易方程的解法.解题步骤.书写格式以及检验方法。

3.进一步感受数学与现实生活的联系，会列方程解决一些简单的实际问题。

用字母表示数

一、填空。

1.用含有字母的式子表示下面的数量关系。

①比9少a的数：_______

2.根据运算定律，在横线上填上适当的字母和数。

①a×(b×c)=(___×___)×c

②(a+8)×b=a×___+___

③a+3.5+b=a+___+3.5

④(x+y)×10=___×___+___×___

3.用字母表示下列计算公式。

①长方形的周长：___________

②梯形的面积：__________

③圆的面积：__________

④圆锥的体积：__________

4.学校思维训练组有20人

（1）口语交际组比思维训练组多a人，口语交际组有（ ）人。

（2）航模组比思维训练组少b人，航模组有（ ）人。

（3）合唱组的人数是思维训练组的c倍，合唱组有（ ）人。

（4）舞蹈组的人数比航模组多5人，舞蹈组有（ ）人。

5.一个等腰三角形的一个顶角是x°，那么它的一个底角是（ ）°。

6.南通到上海水路长154千米，一艘轮船从南通出发到上海，每小时行vkm，7小时后距南通（ ）km，距上海（ ）km。

7.与a相邻的两个整数分别是（ ）和（ ），这两个数的和是（ ）。

8.公共汽车上原来有40人，到新华路站下去x人，又上来y人，现在车上有（ ）人。

9.一本书有y页，李灵每天看书5页，x天看了（ ）页，还剩（ ）页没看。

10.王名今天去商店买了1块橡皮和3本笔记本，每块橡皮m元，每本笔记本n元，王名一共付出（ ）元。

11.果园里有桃数x棵，苹果树比桃树的3倍少20棵。果园里有苹果树（ ）棵，苹果树比桃树多（ ）棵。

12.学校体育室买回a个乒乓球和b个羽毛球，一个乒乓球2元，一个羽毛球3元，买羽毛球比乒乓球多用去（ ）元，如果a=8,b=10时，那么具体是（ ）元。

二、选择。（在括号里填上表示正确答案的序号。）

③m的5倍减去2.5：___________

1.三角形的面积为S，底边上的高为h，底边是（ ）。

A.S÷h B.2S÷h C.S÷2h

2.妈妈今年a岁，明明今年b岁，10年后妈妈比明明大（ ）岁。

A.a-b+10 B.b-a C.a-b

3.当a=5、b=4时，ab+3的值是（ ）。

A.5+4+3=12 B.54+3=57 C.5×4+3=23

4.一个奇数用m表示，它后面一个相邻的奇数用式子表示是（ ）

A.m-2 B.m+2 C.2m

A.a=10 B.a<8 C.a<11

三、解答。

1.一辆汽车，每小时行驶a千米，上午行驶4小时，下午行驶了b千米。

（1）用式子表示这辆汽车行驶的千米数。

（2）当a=80、b=200时，这辆汽车行驶了多少千米？

2.用卡车来运一堆煤，上午运了m车，下午运了n车，每车装5吨。

（1）用式子表示这天一共运了多少吨。

（2）当m=3、n=4时，这天一共运了多少吨？

等量与方程

一、化简下面各式。

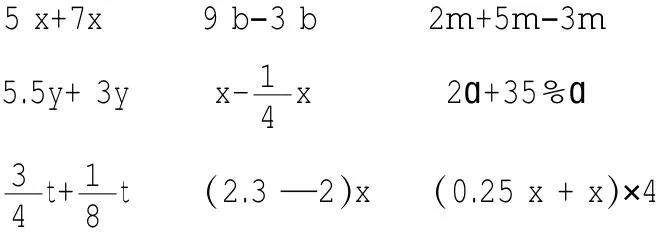
二、判断。（在括号里正确的打“√”，错误的打“×”。）

1.方程都是等式，但等式不一定是方程。( )

2.方程的解和解方程是一回事。 ( )

3.5.5 x+1.3 x=88是方程。（ ）

4.7 x=0，这个方程没有解。 （ ）

三、解下列方程。

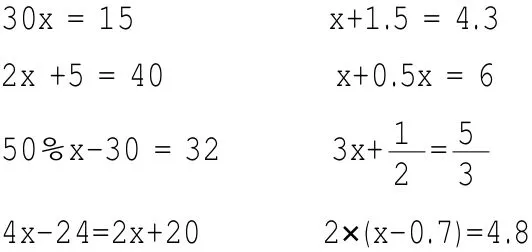
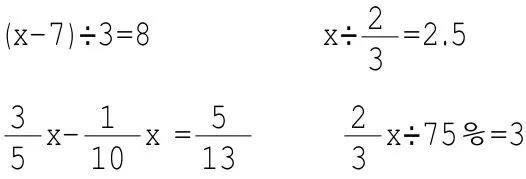
用方程解决问题

一、列出方程并求方程的解。

1.一个数的5倍加上3.2，和是38.2，求这个数。

2.3.4 比x的3倍少5.6，求x。

3.一个数的4倍加上它的5倍得135，求这个数。

4.15 加上一个数的2倍，等于34的一半，求这个数。

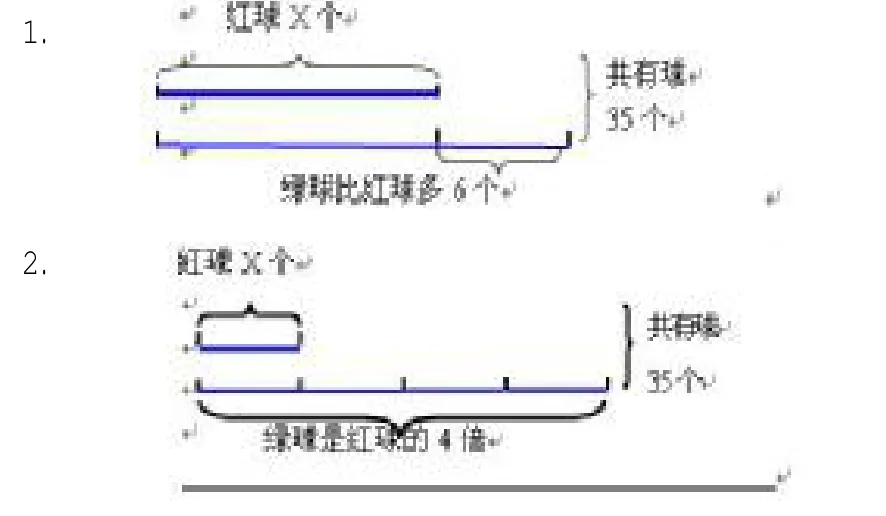
二、根据图意只列出方程

三、解决问题。

1.红花和黄花共15朵，红花的朵数比黄花的2倍还多3朵，红花和黄花各多少朵？

2.甲、乙两地相距693km，一辆客车和一辆货车同时从两地开出，相向而行，已知货车每小时行45km，客车的速度是货车的1.2倍，客车开出几小时后两车相遇？

3.甲.乙两车间原来人数相等，因工作需要，从甲车间调24人到乙车间。这时甲车间人数是乙车间的甲、乙两个车间原来各有多少人？

4.10 元一张与5元一张的钱共175元，10元的张数是5元张数的3倍。求两种票面额的钱各有多少元？

5.长方形操场的长与宽相差40m，某同学沿操场边跑了3圈，共1200m。这个操场的长和宽各是多少m？

6.甲、乙、丙三数的和是88，甲数比乙数的2倍多4，乙数是丙数的3倍，求三数各是多少。

8.

9.