多分辨率小波分析在GIS线状要素简化中的应用
黄 娟,程耀东
(兰州交通大学数理与软件工程学院,兰州 730070))
多分辨率小波分析在GIS线状要素简化中的应用
黄 娟,程耀东
(兰州交通大学数理与软件工程学院,兰州 730070))
线要素化简一直是自动制图综合中的重要研究内容。利用小波分析的多分辨率原理和Douglas算法,对线状要素进行平滑和综合,实现了线状要素的空间多尺度表达。并对实际数据进行实验,结果表明,此方法不仅能够达到曲线化简的目的,而且能够保持化简前后的视觉效果和原始数据的特征。
小波分析;小波多分辨率分析;Douglas算法;线状要素
0 引言
空间数据的多尺度表达问题是GIS研究的重点,也是地图自动综合的瓶颈。地图矢量数据都可用线状图形来表达,这就使得多尺度研究的焦点主要集中在线要素自动简化模型的建立。许多学者已经对此问题做了大量的研究,Li Zhi-lin和Openshaw(1992)提出的基于客观综合的自然规律的线划要素化简的方法[1];VisvaLingam和Whyatl(1993)提出的基于最小面积的重复式点删除方法[2];Salfeld(1999)提出的基于逻辑一致的Douglas算法[3];郭庆胜(2002)提出的渐进式化简算法[4];武芳(2002)提出的基于遗传算法的线要素化简算法[5]等。线化简的算法虽然很多,但很多都不能有效保留原始曲线的形态结构特征且曲线的光滑度差,造成化简前后曲线形态歪曲。本文在研究小波分析的多分辨率分析原理的基础上,将小波分解后的频域分析和Douglas算法相结合,建立一种线要素简化的新模型,并对实际数据进行实验,对简化前后的数据作比较,结果表明,该方法适合于线状要素数据简化,能够很好的保持原始数据的结构特征。
1 线状要素的化简原则
线状要素是地图上大量存在的最基本的地图要素,它的综合主要包含两个方面:数量的选取和形状的化简。在手工制图的情况下,形状的化简主要依靠人的大脑和感官的作用,来把握它的形状结构特征,从而根据线划化简的基本原则对其进行综合处理。
在大比例尺的地图综合中,线要素的化简作为同一线划在不同尺度下图形的再表达,在选取一个有效的化简算法的同时,还要遵循地图制图的一些基本原则。其基本原则为:①保持弯曲形状的基本特征,即总的图形的相似性;②保持弯曲的特征转折点的精确性;③保持不同弯曲程度的对比。
2 多分辨率小波分析原理与 GIS图形数据的多尺度表达
2.1 多分辨率小波分析原理[67]
定义:设L2(R)是一平方可积函数空间,{Vj,j∈Z}是L2(R)的一列函数子空间,R是实数集,Z是整数集,若{Vj,j∈Z}满足
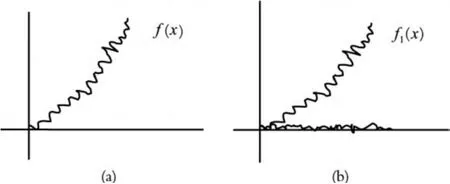
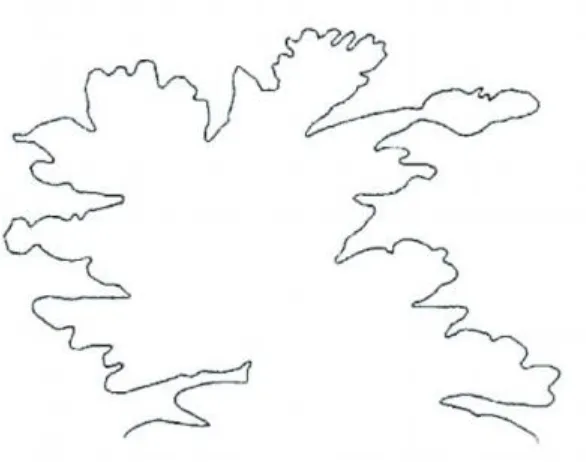
(1)单调性:对 Πj∈Z,有Vj (3)独立性:∩Vj={0}; (4)缩放性:f(x)∈VjΖf(2x)∈Vj+1; 设以Wj表示分解中的高频部分Dj,Vj表示分解中的底频部分Aj,则Wj是Vj在Vj+1中的正交补,即 2.2 基于小波分析的GIS图形数据多尺度表达[8- 10] 基于小波的特点,将平方可积空间L2(R)看成某地理空间,f(x)看成该空间的各种信息,则{Vj,j∈Z}可看成L2(R)在不同比例尺即不同分辨率下的地理空间模型,{Wj, j∈Z}则为相应的细节信息;也就是说,如果将空间L2(R)看成某地理空间在特定比例尺下的GIS图形数据模型,f(x)是其上图形要素,{Vj,j∈Z}则可看成在没有进行相应的比例尺缩小变换情形下的多比例尺GIS图形数据模型。在应用中,设L2(R)=V0,可把从V0出发,把尺度函数(X)表示成V1,V2,…,Vj的过程,可以看成是一种比例尺的 GIS图形数据模型V0,派生出多比例尺GIS图形数据模型V1,V2,…,Vj的过程,此过程实际上是一种基于多分辨率分析的GIS图形数据的表达过程。在自动综合过程中,一般要分要素或分内容进行,不失一般性,不妨我们设V0只包含一种图形要素,如线状要素 y=f(x)。 2.3 多分辨分析与线状要素的关系 定义:设L2(R)是一平方可积函数空间,{Vm,m∈Z}是L2(R)的一列函数子空间,R是实数集,Z是整数集,若{Vm, m∈Z}满足: 设比例尺为1:M的GIS图形曲线用l=f(x)来表示,对此曲线采用有限点进行逼近,得到离散化表达式{f(xi)}, i=1,2,…,再经过适当的插值和一系列坐标变换,其离散化表达式将变为V0={f(n)},n=1,2,…,2N。 式(5)右边的第一项是曲线l=f(x)在V1中的表达式,记作A1f(x),第二项是曲线l=f(x)相对于V1在V0中的细节信息,记作W1f(x)。 又V1=V2+W2,则 式(6)右边的第一项是曲线l=f(x)在V2中的表达式,记作A2f(x),第二项是曲线l=f(x)相对于V2在V1中的细节信息,记作W2f(x)。因此一般地,有曲线l=f(x)在Vm中的表达式Amf(x)和其在Vm-1中的细节信息Wmf(x),即 3.1 基于传统小波分析的线状要素简化[11] 用正交小波的分解公式(3),对一线状要素 f(x)进行小波分解,如图1,得到低频部分 f1(x)和高频部分 g1(x),显然,f1(x)保留了原始曲线的总体轮廓特征,因此 f1(x)可看做 f(x)的近似逼近,而传统方法就是把 f1(x)作为 f(x)的压缩数据,但此方法将线状要素的所有点包括特征点,发生了位移的变化,这将使原地性线,地貌形状结构特征遭到破坏。高频部分 g1(x)却包含着 f(x)的主要特征信息,在高频部分的数据中,绝对值较大的部分对应着原始数据中奇异性较大的数据点,即线状要素中特征点所在的位置,接近于零的部分对应着原始数据中奇异性非常小的数据点,即线状要素中一些冗余数据点所在的位置,去掉冗余点,可达到压缩优化原曲线的目的。 图1 曲线分解图 3.2 基于小波分析的Douglas算法简化线状要素 为了找回原数据L0中的特征点,去掉压缩数据L1中的非特征点,使线状要素得到真正的压缩优化,可将小波分解后的域频分析,Douglas算法以及曲率分析相结合。具体算法如下。 (1)利用小波分析对线状要素进行压缩优化。 ①取三系数的小波基,对原数据L0进行小波分解,得到低频部分数据 f1(x)和高频部分数据 g1(x); ②选取适当的阈值ω,如果|g1(x)|>ω,则为特征点,并将特征点插入到 f1(x),否则为冗余点,直接去掉; ③把插入了特征点的低频部分数据 f1(x),作为一次小波变换后的数据L1。 (2)再次处理L0中的数据。 在L1中,把介于间隔数据 pi,pi+2之间L0中的数据,用Douglas算法,求出 pi,pi+2中的特征点 pm(即 pm为到直线pipi+2距离最远的点)。 (3)计算 pi+1,pm的曲率。 首先求出点 pi+1,pm到直线pipi+2的距离 di+1,dm,并求出|pipi+2|的长度 d,然后计算点 pi+1,pm的曲率,即 (4)比较曲率 pi+1,pm的大小,筛选特征点 pi+1和 pm。 若ρi+1<ρm,则 pm就是比pi+1奇异性更大的数据点,在L1中用点 pm代替 pi+1。 小波变换后的数据L1经过上述处理,将会去掉其中的非特征点,补回原数据L0中丢失的特征点,从而使线状要素得到真正的压缩优化。 基于上述算法原理和步骤,结合地图数据表达的特点,下面对一原始等高线图形进行试验,图2为原始数据,有1 672个点,图3为经小波分析处理的压缩数据,有531个数据点,压缩比为31.76%,图4为处理前后的叠加数据。 图2 原始数据 图3 处理后的数据 图4 处理前后的叠加数据 由实验可知,该方法适合于制图综合的线状要素的处理和应用,通过实验结果得出,先用小波分析的多分辨率分析将曲线分解为高频部分和低频部分,然后判断高频部分的数据是否为特征点,若是,则将特征点插入到低频部分数据f1(x),得到压缩数据L1,最后利用Douglas算法对压缩数据L1进行再处理,得到最终的数据L0。在处理过程中,为了保证曲线的基本形态不发生变化,本文采用保留端点处的信息,仅对中间的数据进行处理。通过叠加可以看出简化后的视觉效果和精度。 本文利用小波分析的多分辨率分析原理,给出了小波分析与GIS图形数据多尺度表达的关系,提出了一种将多分辨率分析,Douglas算法和曲率分析相结合的一种新型算法,实现了线状数据的压缩优化。随着制图自动综合理论与技术的不断完善,多小波的多分辨率分析将在间线状要素制图综合中发挥重要的作用。 [1] Zhilin Li,Stan Openshaw.Algorithms for automated line generalization based on a natural principle of objective generalization[J].Geographical Information Systems,1992,6(5):373-389. [2] M.Visvalingam,J.D.Whyatt.Line generalization by repeated elimination of the smallest area[J].The Cartographic Journal,1993,30(1):46-51. [3] Salfeld A.Topologically consistent line simplification with the douglas-peuker algorithm.Cartography and Geographic Institute Science,26(1):7-18. [4] 郭庆胜.线状要素图形综合的渐进方法研究[J].武汉测绘科技大学学报,1998,23(1):52-56. [5] 武芳,钱海忠,邓红艳,等.面向地图自动综合的空间信息智能处理[M].北京:科学出版社,2008,164-170. [6] 关履泰.小波方法与应用[M].北京:高等教育出版社, 2007.7:54-93. [7] 邸继佂.小波分析原理[M].北京:科学出版社,2010: 77-93. [8] 吴凡,祝国瑞.基于小波分析的地貌多尺度表达与自动综合[J].武汉大学学报:信息科学版,2001,26(2):170 -174. [9] 吴纪桃,王桥.小波理论用于地图数据处理中若干理论问题的探讨[J].测绘学报,2002,31(3):2452-248. [10] 宋卫卫,朱顺刚,欧宗瑛,等.基于形状相似性和曲线化简的统计形状模型建立[J].光电子·激光,2008, 19(9):1231-1235. [11] 吴纪桃,王桥.小波分析在 GIS线状数据图形简化中的应用研究[J].测绘学报,2000,29(1):71-75. (责任编校:李高峰) Application of Multi-Resolution Wavelet Analysis in GISL inear Element Simplification HUANGJuan,CHENG Yao-dong Simplifying linear elements is always the important research in automatic drawing generalization.With the principle of multi-resolution analysis and Douglas algorithm,linear elements have been smoothed and synthesized and finally linear element spatial multi-scale expression is realized. The results show that this method can not only achieve the purpose of simplifying the curve but also maintain visual effect and the characteristics of linear elements before and after simplification. wavelet analysis;wavelet multi-resolution fatio analysis;Douglas algorithm; linear element P208;P283.7 A 1672-349X(2010)06-0013-04 2010-10-15 国家自然科学基金(40871208) 黄娟(1983-),女,硕士研究生,主要从事多尺度地理空间单线目标的相似度描述与计算模型的研究。



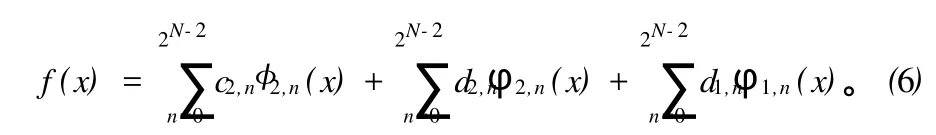

3 基于小波分析的线要素简化
4 实例分析

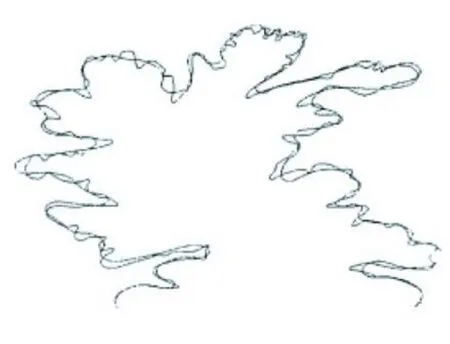
5 结束语
(School of Mathematics,Physics and Software Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)

