基于轴承负荷的转子轴承系统建模与试验研究✳
孙虎儿,杨兆建,梁群龙,庞新宇
(1.太原理工大学机械工程学院,山西太原 030024;2.中北大学机械工程与自动化学院,山西太原 030051)
0 引 言
对转子系统故障的研究是为了防止系统可能出现的具有危害性的破坏.近 20年来,转子的振动测试技术和故障诊断技术发展很快,很多技术成果已经在现场使用,而且使用效果也很好.随着科学技术的不断发展,在转子的测试和诊断技术方面,涌现了不少新技术、新分析手段,如铁谱分析仪、全息谱技术、超声波技术等.但是,通过研究发现,如果转子轴承系统发生故障,首先会表现在轴承的负荷上.换句话说,如果轴承负荷发生了变化,则预示了转子轴承系统发生了一定的故障,再以其他方法辅助检测,可很快判断其故障性质和类型.
1 考虑轴承负荷作用的转子系统建模
1.1 系统建模
根据目前我们试验台[1]的情况,可建立如图1所示的力学模型[2].从图1中可以看出,该模型的建立,主要考虑了电机、联轴器、轴、轴承等的耦合作用,结构上比较复杂,求解难度大,而且有些因素并非主要因素.另外,在建模时引入了轴承负荷,轴承负荷[3-4]主要是由转子不对中、摩碰、油膜涡动等转子的故障而引起.因此如何建立合理的力学模型显得尤为重要,力学模型的求解过程也是寻求轴承负荷与振动信号[5-8]的耦合关系的过程,为此对图1所示的力学模型作了一些必要的简化.

图1 考虑轴承负荷的转子振动的力学模型Fig.1 Model of lateral vibration of the rotor system on bearing load

图2 轴承转子振动的简化力学模型Fig.2 Simplified dynamic model of vibration of the rotor system
1.2 模型简化
为求解方便,在考虑主要因素的前提下,有意识地简化了一些因素,通过简化得到如图2所示的力学模型.在简化模型中,作了一些必要的等效,等效轴的时候作了两个方面的考虑:一方面将轴等效为弹簧;另一方面将其看作刚性为∞,具有一定长度和质量的杆.将轴和圆盘的质量等效为 m1,油膜刚度和轴在长度方向的刚度串联后等效为刚度 k1,c1代表油膜产生的阻尼系数.m2是左支撑的质量,轴承座刚度、螺栓刚度和载荷传感器的刚度串联后的等效刚度为 k2.同理,右支撑的各个量也可求得.F1,F2是通过载荷传感器测得的.
1.3 振动方程的建立
通过图2所示的力学模型,根据达朗贝尔原理建立了二自由度三质体振动方程.

2 实测载荷分析
2.1 载荷传感器
转子系统的载荷测量一直是个难题,其难度主要在于载荷传感器本身很难布置,这也是有关轴承负荷状态检测几乎处于空白的主要原因.杨兆建教授发明的载荷传感器很好地解决了这一问题,其主要原理是再在载荷传感器上打上盲孔,在盲孔中贴应力应变片,通过测传感器本身微小的变形量来检测载荷的变化.传感器布置于轴承座下面,在建模时可将传感器本身看作一个具有有一定刚度的弹簧.
2.2 实测载荷
通过载荷传感器实测可得到载荷的实际变化规律,图3,图4分别为图1中右支撑和左支撑的载荷变化规律曲线,经过拟合可得到载荷 Fy1,Fy2.

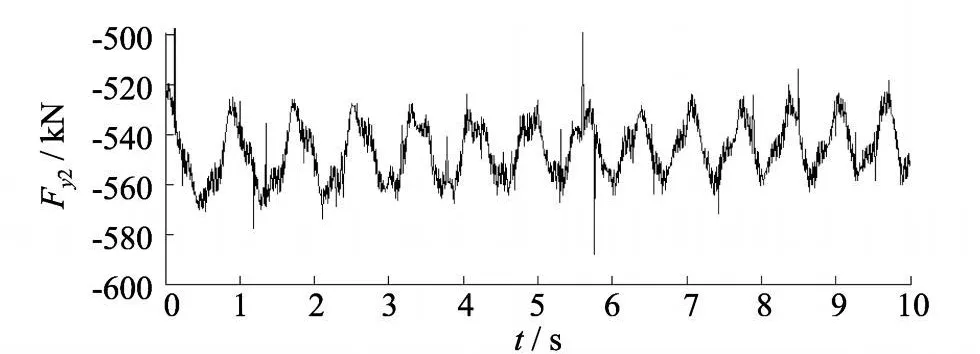
图3 右支撑实测载荷曲线Fig.3 Detected load curve of right support

图4 左支撑实测载荷曲线Fig.4 Detected load curve of left support
3 仿真与实测振动信号对比分析
3.1 仿真结果
将实测载荷和系统各个参数代入方程(1),用数值法求解,得到振动信号的仿真图像.对照图5,图6可以看出,左支撑的加速度幅值要大于右支撑的加速度幅值,分析其原因,主要是左右支撑上的载荷不同(即 F0不同)而造成的.另外,左支撑的加速度波形“拍振”[9]效应更加明显,原因主要是由于左支撑上作用的载荷频率更接近于转子的振动频率.

图5 左支撑加速度仿真曲线Fig.5 Simulation acceleration curv e of left support

图6 右支撑加速度仿真曲线Fig.6 Simulation acceleration curve of right support
3.2 实测振动信号
通过在轴承座上加装加速度传感器,可测得各轴承座的实时加速度.但是,加速度传感器布置于轴承座上,当转子工作时,轴承座会发生一定的振动,而传感器本身也会随着一起振动,因此测到的信号就会混入较为复杂的噪声信号.故在实际分析时,有必要对振动信号进行去噪处理,本文采用小波[10]进行了降噪处理.
通过对比左右支撑的实测加速度曲线(图7,图8),发现了预仿真曲线的类似之处.首先,左支撑上的加速度幅值要大于右支撑上的加速度幅值;其次,左支撑的“拍振”效应明显高于右支撑.

图7 左支撑实测加速度曲线Fig.7 Detected acceleration curve of lef t support

图8 右支撑实测加速度曲线Fig.8 Detected acceleration curve of right support
3.3 对比分析
对照图5和图7,会看到它们的振动周期基本一致,加速度幅值相同,在相同的时间都出现了尖峰幅值,验证了建模的正确性.对照图6和图8,也会发现相同的规律.
通过上述分析,基本可以看出这样的规律:振动信号中伴随有强迫振动,而且左右支撑振动加速度幅度不同,振动周期也略有不同.再看图3,图4所示的载荷变化规律,左右支撑的载荷都呈现周期性变化,而且载荷波形的相位并不相同.在同一个轴的不同的两个支撑上出现了载荷幅值不同、相位不同而且同一时刻载荷方向相反.这样的情况只能说明一点,即转子的标高发生了偏差或转子不对中[11].这是因为建模时我们充分考虑了电机的影响(如图1),也就是说可以将该单跨转子系统看作一个三支撑的系统,电机可看作一个支撑,但简化模型时,把电机因素考虑在 Fy1里了,所以出现了 Fy1大于 Fy2的情形.
4 结 论
本文在考虑轴承负荷的条件下对转子系统进行了建模分析,并对两个支撑的振动信号进行了仿真研究.搭建了基于载荷测量的转子实验系统,实测了左右支撑的载荷和振动信号.通过比较和分析得出如下结论:
1)仿真得到的加速度信号和实测的加速度信号峰值呈周期性变化,周期相同;支撑振动是由轴承负荷所引起的强迫振动与其它振动信号叠加而成,而支撑振动的特性是受轴承负荷影响的.
2)轴承负荷的变化可以作为轴承转子系统状态估计的一个重要条件,尤其是轴承负荷对于诊断转子由于标高变化而引起故障和不对中引起的故障效果较为明显;
3)在建模中忽略了一些因素(如阻尼等),造成了仿真结果与实验结果有些偏差,在下一步研究中要不断完善.
[1]席文奎,杨兆建,梁群龙.多支承转子轴承系统试验台动力学设计[J].太原理工大学学报,2007,38(5):398-400,404.Xi Wenkui,Yang Zhaojian,Liang Qunlong.Dynamic design of multi-support bearing-rotor system test-bed[J].Journal of Taiyuan University of Technology,2007,38(5):398-400,404.(in Chinese)
[2]Chen Z S,Yang Y M,Hu Z,et al.Detecting and predicting early faults of complex rotating machinery based on cyclostationary time series model[J].Journal of Vibration and Acoustics,2006,128:666-671.
[3]孙军,桂长林,汪景峰.基于整体曲轴梁单元法的曲轴变形和轴承负荷计算[J].农业机械学报,2008,38(6):6-9.Sun Jun,Gui Changlin,Wang Jingfeng.Study on calculation of crankshaf t deformation and bearing load based on whole crankshaft beam-element method[J].Transactions of the Chinese Society for Agricultural Machinery,2008,38(6):6-9.(in Chinese)
[4]杨兆建,王勤贤,黄广龙,等.大型汽轮机轴承负荷传感器长期稳定性试验研究[J].仪表技术与传感器,2003(2):46-47.Yang Zhaojian,Wang Qinxian,Huang Guanglong,et al.Experiment study on the long-term stability of bearing load cell in large turbine-generator sets[J].Instrument Technique and Sensor,2003(2):46-47.(in Chinese)
[5]张靖,闻邦椿.两端支座松动转子系统的频率特性分析[J].中国机械工程,2008,19(1):68-71.Zhang Jing,Wen Bangchun.A study of frequency characteristics of rotor system with pedestal looseness at two supports[J].China Mechanical Engineering,2008,19(1):68-71.(in Chinese)
[6]王宗勇,龚斌,闻邦椿.激励幅值突变转子系统的动力学研究 [J].振动与冲击,2008,27(3):55-59.Wang Zongyong,Gong Bin,Wen Bangchun.Dynamics of rotor system under sudden change of excitaion magnitude[J].Journal of Vibration and Shock,2008,27(3):55-59.(in Chinese)
[7]李小彭,宫照民,刘杰,等.多跨故障转子系统动态特性有限元仿真研究 [J].东北大学学报,2008,29(2):250-253.Li Xiaopeng,Gong Zhaomin,Liu Jie,et al.Simulation of dynamic characteristics of faulty multi-span rotor system through FEA[J].Journal of Northeastern University(Natural Science),2008,29(2):250-253.(in Chinese)
[8]蓝柏云,张雷,秦宗慧.空冷 135 MW汽轮发电机转子横振特性研究[J].机械强度,2006,28(1):127-131.Lan Baiyun,Zhang Lei,Qin Zonghui.Study on rotor lateral dynamic characteristics of 135 MW air-cooled turbine generator[J].Journal of Mechanical Strength,2006,28(1):127-131.(in Chinese)
[9]韩军,高德平,胡绚,等.航空发动机双转子系统的拍振分析 [J].航空学报,2007,28(6):1369-1373.Han Jun,Gao Deping,Hu Xuan,et al.Research on beat vibration of dual-rotor for aero-engine[J].Acta Aeronautica Et Astronautica Sinica,2007,28(6):1369-1373.(in Chinese)
[10]陈淑琴.基于小波包分析的道路信号加速度特征谱提取[J].中北大学学报(自然科学版),2007,28(4):369-372.Chen Shuqin.Extracting eigenvalue and eigenvector of the road signals based on wavelet packet′s analysis[J].Journal of North University of China(Natural Science Edition),2007,28(4):369-372.(in Chinese)
[11]付波,周建中,彭兵,等.固定式刚性联轴器不对中弯扭耦合振动特性[J].华中科技大学学报,2007,35(4):96-99.Fu Bo,Zhou Jianzhong,Peng Bing,et al.Coupled lateral and torsional vibration properties of parallel misaligned fixed rigid couplings[J].Journal of Huazhong University of Science and Technology(Nature Science Edition),2007,35(4):96-99.(in Chinese)

