运用MATLAB实现换热网络动态特性的通用自动求解

姜 涛,崔国民

(上海理工大学热工程研究所,上海 200093)

0 引 言

通常,一个换热网络是一个化工系统的子系统,所以换热网络物流的供给性质例如输入温度和流率常常受化工过程中其他因素的影响而偏离它们的标准值。如果标准值要求保持不变或在一个给定的范围之内,当供给性质变化时,就需要一个控制系统[1]。换热设备的动态特性一直以来是一个研究课题,它是分析、设计和改进换热设备及其控制系统的重要依据,因此受到众多学者的关注,其中换热设备的传递特性显得尤为重要[1～3]。但是到目前为止,研究人员主要把目光集中于单体换热器的动态特性研究,这方面的成果层出不穷,推导得到了各种形式的传递函数。而对于换热网络动态特性的研究,目前主要针对于某些特定的热力系统或结构,而且鲜见关于换热网络传递特性研究方面的资料。李政[4]等在国产200 t/h循环流化床锅炉建模与仿真工作中开发了一种复杂换热器系统动态特性的计算方法;杨德明[5]以能量守恒为基础,建立了换热网络的机理动态数学模型。目前这些数学模型及表达式的通用性和实用性都较差,尚缺乏一种能普遍广泛运用的通用求解方法,因此换热网络动态特性的研究具有十分重要的意义。

本文基于信号流图,提出一种快速求解换热网络动态特性的通用方法,该方法以单体换热器为模块,连接各个换热器形成换热网络的信号流图,以换热器入口信号是否准备好作为模块计算依据,采用以模块为核心的动态求解策略依次求解各个换热器,直到所有换热器计算完毕,最终获得换热网络流体出口温度变化对入口参数变化的传递函数。同时本文运用MATLAB编制了自动求解程序,MATLAB强大的符号运算功能使得计算方便简洁,速度快,且通用性强。

1 单体换热器的处理

在工业过程中,大部分被控对象为具有纯滞后的一阶或二阶惯性环节[6]。根据换热器的特点,其动态数学模型可以用具有纯滞后的一阶惯性环节表示,其传递函数表示为

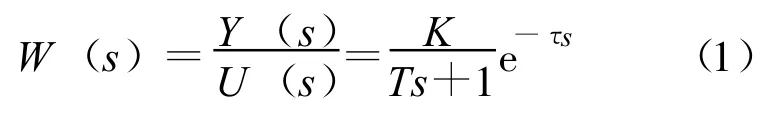
式中:W(s)为出口参数变化与入口参数变化的比值;U(s)和Y(s)分别为换热器输入和输出参数变化量的拉氏变换;T,K,τ为3个决定换热器动态响应过程的动态特性参数,其中,T为时间常数,反映流体参数变化的快慢,K为静态放大系数,τ为滞后时间。这3个动态特性参数可以通过理论分析计算或曲线拟合得出,对于不同的入口参数变化,动态特性参数也不同,因此有24个不同参数。当入口参数变化不大时,出口参数的变化可看成是各入口参数引起的变化的线性叠加,这样单体换热器冷热流体出口温度的变化可写成:

此时换热器即相当于一个4输入 4输出系统,如图1(a)所示,将其转换成信号流图形式如图1(b)所示。

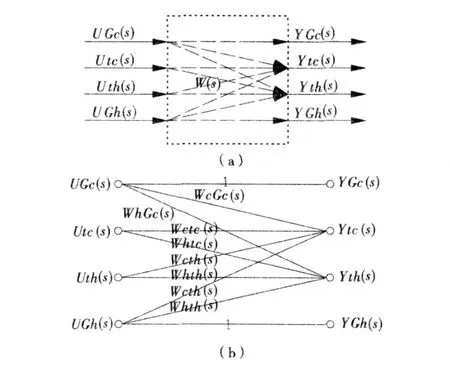
图1 单体换热器传递函数模型及其信号流图Fig.1 Transfer functions and signal flow graph of heat exchanger

在MAT LAB中创建一个二维数组DANAMICPA存放这些动态特性参数的具体数值,该数组分24列,行号代表换热器号,以供计算所需。

2 换热网络建构及识别

如上所述,每个单体换热器都可转换成信号流图形式,这样各个换热器连接成的换热网络也就可以转换成信号流图的形式。在换热网络中,同股流体流经的各个换热器,流体的入口参数变化为上一个换热器的出口参数变化,也就是说,上一个换热器的出口信号变化输入给了下一个换热器,依据这种传递关系,一个2×2一级换热网络可以用信号流图表示成如图2所示的结构。

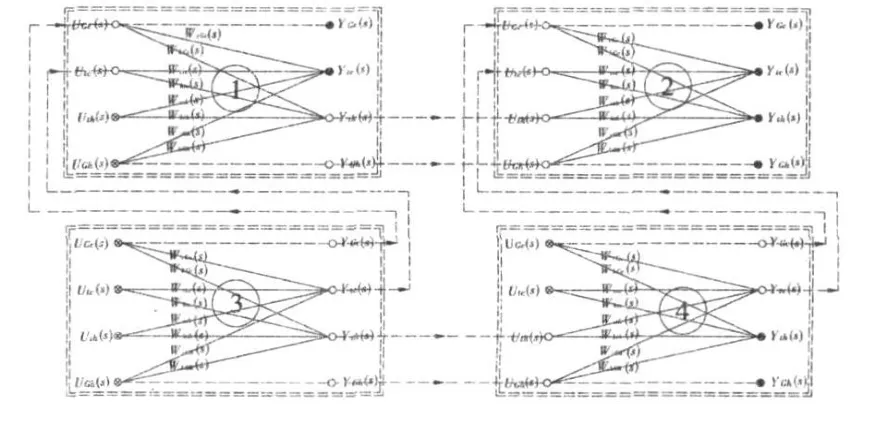
图2 换热网络超结构模型及其信号流图Fig.2 Signalflow graph of a 2×2 heat exchanger network

如图所示,虚框内为一个换热器的信号图,即一个模块,圆点表示信号节点,实线表示节点间的传递函数。各个模块间用虚线连接,表示连接管道,此上不考虑热量损失,只考虑时间滞后。

本文基于单体换热器的信号图,采用部件模块连接的方式构建换热网络的信号流图。将单体换热器看成一个小模块,模块入口信号为流入该换热器的流体信号变化的s域表达式,该表达式乘以传递函数即为出口信号变化的s域表达式,又作为该股流体流向的下一个换热器的入口信号。这样各个换热器形成一个个小模块,按照流体间的实际换热匹配和流体先后顺序,将各个单体换热器的出、入口信号通过连线 (管道)连接起来,形成换热网络的信号流图。这种方法具有直观、方便以及通用性强的特点。

网络识别采用索引矩阵法,矩阵行号表示换热器号,即单元模块号。矩阵分4列,第1列表示该行号的换热器的1热流体从哪个单元模块输出,第2列表示该行号的换热器的热流体输入到哪个单元模块去,第3列表示该行号的换热器的冷流体从哪个单元模块输出,第4列表示该行号的换热器的冷流体输入到哪个单元模块去,0表示给流体为换热网络原始输入流体或最终输出流体。这样,换热网络的结构就能自动识别出来。如图2所示结构的换热网络的索引矩阵的代码为

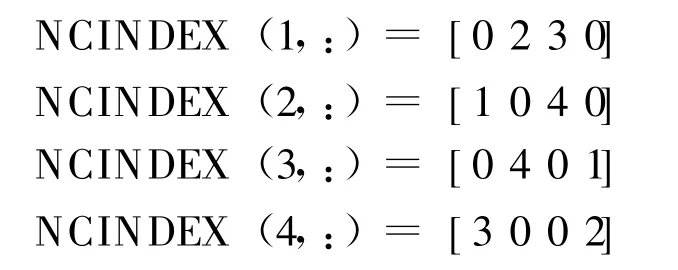
3 自动求解策略

换热网络动态特性的求解建立在获得换热网络传递函数基础上,因此问题关键在于如何获得换热网络的传递函数。

本文采用的求解策略不采用冷流体或热流体作为模拟路径,沿流体流动方向循序求解的方法,而是在求解过程中,采用以模块即换热器为核心的动态求解策略,即在求解过程中,以换热器入口信号是否准备好作为求解的依据,所谓的准备好就是指该入口信号是否为已知,随时计算可以求解的换热器。这种求解策略首先从入口模块——热源和冷源变化信号都已知的换热器入手,对其进行求解,然后将求解得到的出口信号传递到下面的换热器,为下面的换热器求解做准备。继续对各个换热器进行搜索,如果有入口信号都准备好而且没有计算过的换热器,对其进行求解,直到所有的换热器都求解完毕,完成模拟。

首先创建二维矩阵EACHDECIDE判断单体换热器各入口信号是否准备好,该矩阵行号表示换热器号,两列分别表示热流体和冷流体是否准备好,矩阵元素为1表示准备好,矩阵元素为0表示没有准备好。若该换热器的流体为源流体,则元素为1,因为换热网络流体入口参数变化是已知的。

然后创建二维矩阵DECIDE判断换热器是否能计算,同样行号表示换热器号,第1列表示该行号换热器冷、热流体的入口信号是否已知,只有矩阵EACHDECIDE中该行元素都为 1矩阵DECIDE该行才为1,表示换热器准备好可以进行计算;第2列表示该行号换热器之前是否计算过,元素为1表示已经计算过,元素为0表示尚未计算过。

再次给出每个换热器的输入和输出信号矩阵EACHINPUT和 EACHOUTPUT,这两个矩阵为符号矩阵,矩阵元素为有符号 s的表达式,即为换热器入口或出口信号的s域表达式。矩阵有4列,分别表示热流体温度、冷流体温度、热流体流量和冷流体流量的入口或出口信号表达式。

图3给出了程序计算的流程图,这样可以得到所有换热器流体出口温度对换热网络流体入口参数变化的传递函数。如果索引矩阵中第3列或者第4列为0,表示该流体为换热网络最终输出流体,其传递函数即为换热网络该流体的传递函数。得到换热网络的传递函数后,在MATLAB中经拉式反变换,得到时域内流体温度关于时间的表达式,带入数值计算即可观察换热网络的动态特性。

图3 程序计算流程图Fig.3 Calculation flowchart of the program

4 计算实例

本文以化工厂4热、5冷的换热网络为例,网络结构如图4所示,物流数据如表1所示。

各动态特性参数求解采用以下公式。

流体出口温度对入口温度变化放大系数。

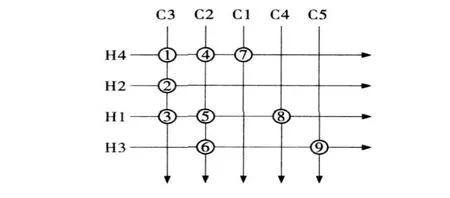
图4 换热网络结构Fig.4 Structure chart of the heat exchanger network

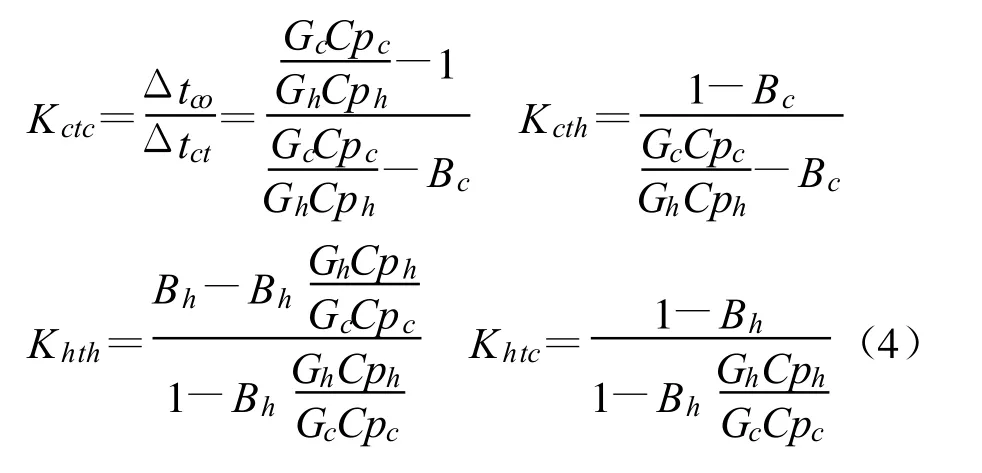
在上面的表达式中,K的下标cth表示冷流体出口温度变化对热流体入口温度变化的放大系数,其它的以此类推。

时间常数:

滞后时间τ:

(1)对流量变化的响应

对于不可压缩流体,当换热器通道内流体的流量发生变化时,试件在整个流程上的换热状况都有改变,因此无论是逆流还是顺流工况,在出口处的温度响应不存在延滞。

(2)对于温度变化的响应

a.在顺流工况下,出口温度的滞后时间取决于两股流体中流速最快的流体,它最先将流体进口温度变化的影响带到出口处。也就是说:τ=L/vmax。

b.在逆流工况下,进口温度发生变化的流体出口温度响应的滞后时间由 τ=L/va来确定,而未发生变化的流体响应的滞后时间为零。

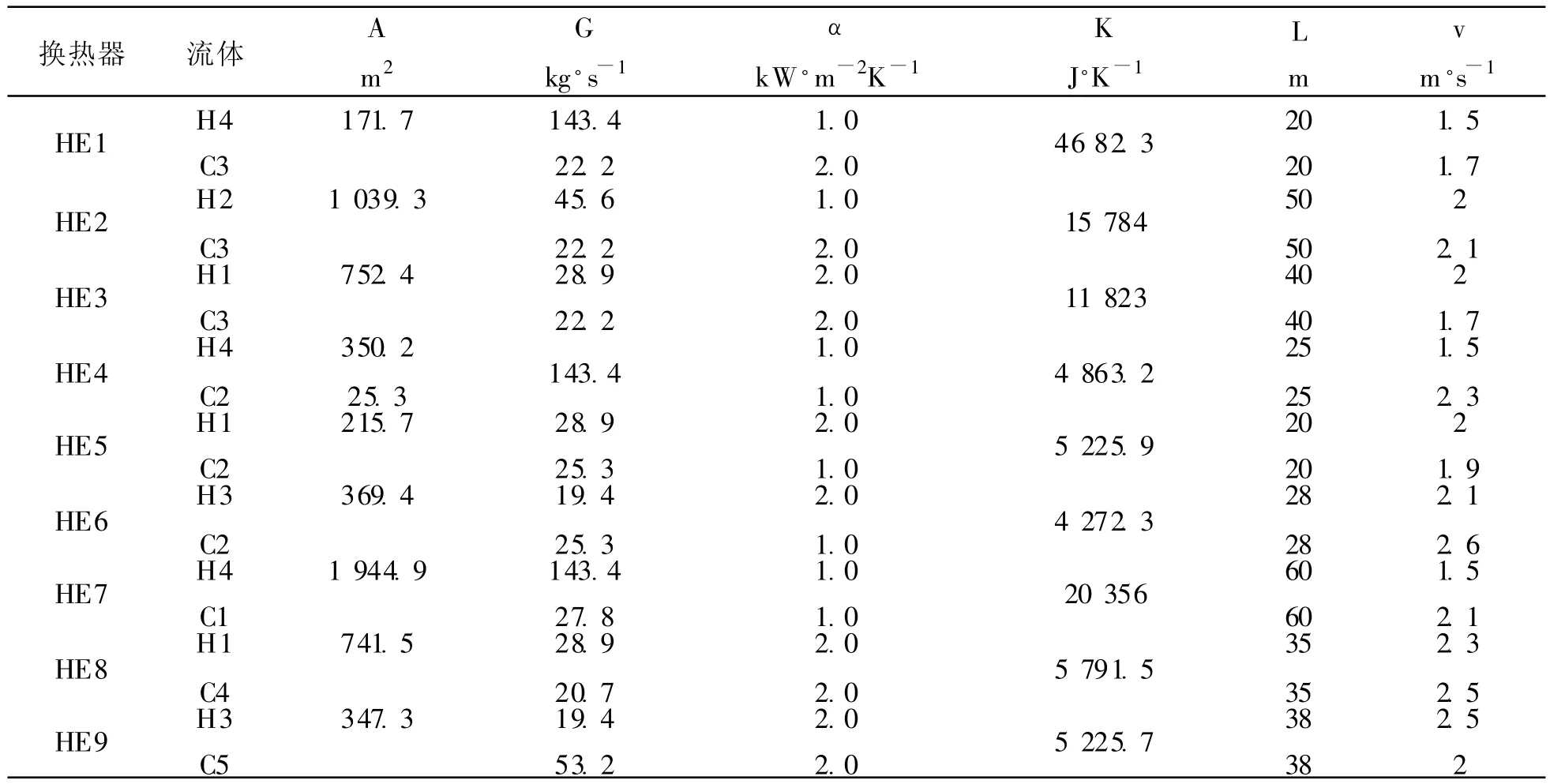
表1 换热器及流体参数Tab.1 Parameter Table of heat exchangers and fluids

当换热网络中热流体1的入口温度发生10℃的上升阶跃时,利用MATLAB编制的自动求解程序,获得换热网络流体出口温度变化对入口温度变化的传递函数,并拉式反变换后得到时域内流体变化表达式如下,同时变化曲线如图5所示。

从图5中可以看出,流体C4,H1,C2,C5,H3出口温度变化响应均存在一定滞后,且滞后时间不同,滞后时间长短与流体的流程有关。由于流体为逆流布置,所以h1入口温度发生变化时,从图4可以看出,流体C3出口温度立即变化,没有滞后。上述各股流体均经过一段时间后达到一个新的稳态值,曲线形状符合实际情况,说明本文提出的方法是可行的。

5 结 论

本文提出了一种换热网络动态特性的通用求解方法,该方法以单体换热器为模块,连接各个换热器形成换热网络的信号流图,以换热器入口信号是否准备好作为模块计算依据,采用以模块为核心的动态求解策略依次求解各个换热器,直到所有换热器计算完毕,最终获得换热网络流体出口温度变化对入口参数变化的传递函数。同时本文运用MAT LAB编制了自动求解程序,MATLAB强大的符号运算功能使得计算方便简洁,速度快,且通用性强。这种求解方法为换热网络的动态特性研究提供了一种新的思路,同时为换热网络的控制奠定的基础。

图5 热流体、冷流体出口温度变化Fig.5 Output temperature change of hot and clod fluids

[1]高维平,杨莹.换热网络的优化改进和控制[J].化工学报,2003,54(7):965-971.

[2]崔国民,张勤,陆贞,等.序贯模块法实现换热网络的模拟[J].工程热物理学报,2006,27(4):682-684.

[3]郭佳,崔国民,王方方,等.换热器动态设计方法研究.工程热物理学报,2007,28(5):865-867.

[4]李政,倪维斗.复杂换热器系统的动态特性计算.热能动力工程,1997,12(4):292-296.

[5]杨德明.换热网络动态数学模型及其求解.江苏工业学院学报,2006,18(1):10-13.

[6]Roetzel W.,Xuan Y.Dynamic Behaviour of Heat Exchangers,Boston:WIT Press,1999.