滑移爆炸冲击荷载作用下矩形复合板的动力响应分析*

靳文强 陈丽萍

兰州交通大学招生就业处(甘肃兰州，730070) 中铁十九局集团有限公司(辽宁辽阳， 111000)

刘京学

兰州交通大学土木工程学院(甘肃兰州，730070)

引言

滑移冲击荷载作用下矩形复合板的动力响应是一个复杂的过程，对于运动荷载作用下梁的动力分析，Fryba、Dieterma和周华飞等人[1]进行了深入研究，取得了很多有益成果。成祥生[2]、黄晓明[3]及候芸等人[4]用不同的方法研究了一些特殊荷载作用下板的动力问题，国外学者Kim 等人[5]和Wu 等人[6]对动力荷载作用下无穷大板的问题进行了较为深入的研究，Karas[7]就对板的撞击问题进行了研究。Vaziri[8-9]还采用超有限元(super finite element)法分析了复合层板和圆柱壳受飞行物撞击的动力响应问题。

对于工程实践中的板所承受的冲击荷载弹性板的动力响应分析，运用薄板横向振动的基本微分方程和三角函数级数展开法，对常速运动面荷载作用下粘弹性地基板进行了分析，求得了板的动力响应的解析解。

1 基本方程及计算模型

1.1 基本方程

薄板横向振动的基本微分方程:

(1)

式中ρ——板件质量密度;

q——单位面积所承受横向动载荷;

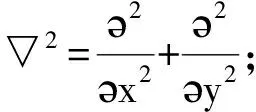
E——弹性模量;

h——板厚;

μ——泊松比。

这是关于挠曲面函数w(x,y,t)的四阶偏微分方程，薄板小挠度振动的基本问题归结为在给定的动荷载及边界条件和初始条件下定解方程。

1.2 边界条件

薄板振动所满足的边界条件和薄板静力问题一样，先列出平行x轴的直线边y=y0的边界条件(平行y轴边界也类似)，然后给出斜边及曲线边的边界条件。若平板边界完全不受力，应该有边缘上各点弯矩、扭矩、剪力为零的三个条件，即

(My)y=y0=0，(Myx)y=y0=0，(Qy)y=y0=0

(2)

由于基本方程(1)为四阶偏微分方程，只能每边满足2个边界条件，而不能满足上述3个力边界条件。为此采用凯尔文—克希霍夫(Kelvin—Kirchhoff)合力边界条件:

(3)

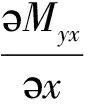
(4)

显然对矩形板振动的研究，最方便是采用直角坐标系(图1)的薄板横向振动基本方程(1)，其相应自由振动方程为:

(5)

图1 薄板横向振动直角坐标模型

对于固有振动的矩形板振型方程:

(6)

引入特征方程[10]:

(7a)

式中a——板长;

b——板宽;

m、n——阶次。

若要对板上任一点上式都成立，并有振型非零解(A≠0)之条件为:

(7b)

可得四边简支矩形板之第(m、n)阶固有频率公式:

(8)

与此频率相应的四边简支矩形板之第(m、n)阶振型为:

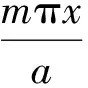
(9)

2 实例计算

工程上应用于气动载荷问题模型。假定有一激发，其波形为阶梯函数，斜扫过板面[10](图1)，波阵面与x轴夹角为β：

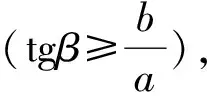
(10)

式中d——激波在x轴方向扫过的距离；

p0——冲击荷载峰值。

有广义力(d≤a)

(11)

对于四边简支板，可算得：

当dtgβ≤b,

(12a)

当dtgβ>b,

(12b)

(13)

在动力响应解中，对于静止初始条件，匀速前进的击波，d(t)=vt，v为荷载移动速度，有解:

(14)

(15)

ZG10Cr13不锈钢屈服强度350MPa，抗拉强度550MPa，采用紫铜作复板，弹性模量E=200 GPa，采用2#岩石炸药，装药密度0.7g/cm3进行爆炸焊接界面基板的应力场模拟计算，基板ZG10Cr13不锈钢的泊松比μ=0.30，分别计算冲击载荷在板的端部和中部的弯曲变形情况(图2)和应力场分布(图3)。

图2 板的变形图

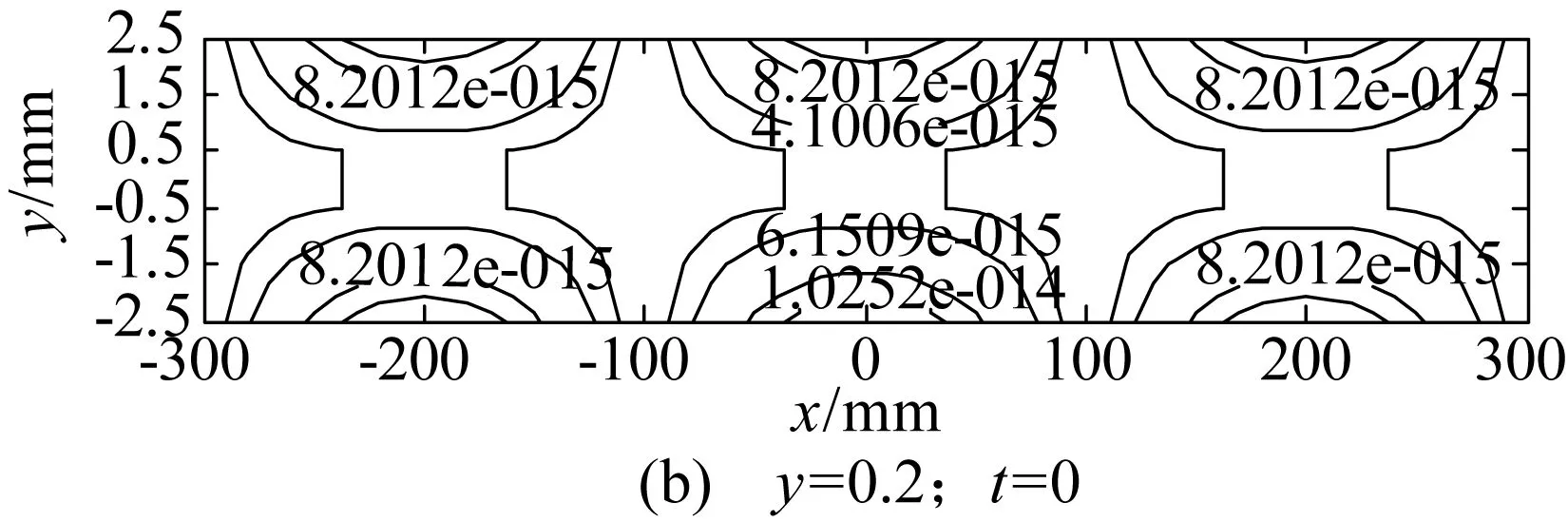
图3 板的应力分布图

通过对板的变形图和应力场分布图分析发现，板的变形和应力均对称分布于板的几何中心，荷载作用位置对变形和应力的影响显著，不论荷载作用在什么位置，板的几何中心和边缘部分相应的挠度变形和应力值相对其它区域较小，而在板的几何中心线和边界之间的中部相应的挠度变形和应力值相对其它区域较大；在板的边界和几何中心线位置扰度变形和应力值变化相对均匀，而在板的几何中心线和边界之间的中部相应的挠度变形和应力值相对集中。

3 结论

(1)对常速运动面荷载作用下粘弹性地基板进行了分析，求得了板的动力响应的解析解，该模型能用来模拟移动冲击荷载作用于薄板时的动力反应、分析评价基板屈服状态。

(2) 移动冲击荷载的速度对板的变形和应力均有一定的影响，板的变形和应力均对称分布于板的几何中心，在冲击荷载的速度超过某一值时，板的变形将出现较为明显的振颤现象。

[1] 周华飞，蒋建群，张土乔. 移动荷载下Kelvin 地基上无限长梁的稳态响应[J]. 浙江大学学报(工学版)，2004， 38(10): 1328-1333.

[2] 成祥生. 弹性地基板由运动荷载引起的反应[J]. 应用数学和力学，1987，8(4): 347-355.

[3] 黄晓明，邓学钧. 运动荷载作用下黏弹性文克勒地基板的力学分析[J]. 重庆交通学院学报，1990，9(2): 45-51.

[4] 侯芸，孙四平，郭忠印. 移动荷载下刚性路面响应的参数影响分析[J]. 同济大学学报，2003，31(1): 31-35.

[5] 孙璐，邓学均. 弹性基础无限大板对移动荷载的响应[J]. 力学学报，1996，28(6): 756-760.

[6] KIM S M，ROESSET J M. Moving loads on a plate on elastic foundation [J]. Journal of Engineering Mechanics，1998，124(9): 1010-1016.

[7] WU C P，SHEN P A. Dynamic analysis of concrete pavements subjected to moving loads [J]. Journal of Transportation Engineering，1996，122(5): 367-373.

[8] Symonds P S，YU Tong-xi. Counterintuitive behavior in a problem of beam dynamics [J]. Journal of elastic-plastic plied Mechanics，1989，52: 517-522.

[9] Genna F，Symonds P S. Dynamic plastic instabilities in response to short-pulse excitation：effects of slenderness ratioand damping [A]. Proceedings of Royal Society of London[C]. London：Printed in Great Britain ，A417，1988.

[10] 曹志远. 板壳振动理论[M]. 北京：中国铁道出版社，1989.