TD-LTE系统中基于奇异值分解的高效波束赋形方法*
(上海贝尔股份有限公司,上海 200070)
1 引 言
作为由我国自主提出的第三代移动通信(3G)标准TD-SCDMA的演进标准, TD-LTE的标准化和面向未来商用的系统试验工作,近年来在无线通信领域内受到了极大的关注[1-2]。目前,TD-LTE系统外场大规模组网试验即将展开。出于TD-LTE系统与TD-SCDMA系统共天线共站址以尽可能降低网络演进成本的考虑,下行链路8发2收的TD-LTE系统已被确定为是一种主流的用于室外覆盖的TD-LTE系统形式[2]。
TD-LTE系统和TD-SCDMA系统同属时分双工(TDD)系统范畴,相对频分双工(FDD)系统具有天然的上下行信道互易性的特点,更便于采用“波束赋形”(或“智能天线”)技术[3-4],用以提高系统下行的传输性能。作为TD-SCDMA系统中的一项特色技术,波束赋形技术能否在TD-LTE系统中进一步地成功演进,并用于实际的网络部署中,提高TD-LTE系统下行传输的系统性能,是TD-LTE系统建设中一项极受关注的热点课题[2]。
在TD-LTE系统中,基站(eNodeB)基于终端(UE)上行两根天线交替发送探测参考信号(SRS)所获得的矩阵信道进行下行波束赋形,相对于基于UE上行固定一根天线发送SRS所获得的向量信道进行下行波束赋形,能获得更好的下行传输性能。在工程上,基于矩阵信道的波束赋形通常采用对信道相关矩阵进行迭代处理的方法获得波束赋形天线加权向量,用于下行波束赋形[5]。但是,为了获得逼近精确的加权向量,需进行多次迭代,复杂度较大且存在由于初始迭代向量选取不当导致迭代不能收敛的风险。
为了克服传统方法复杂度较大且可能不收敛的问题,本文提出一种TD-LTE系统中基于奇异值分解(SVD)的高效波束赋形方法。该方法利用系统终端侧仅有两根天线的系统特性,有针对性地采用下行矩阵信道SVD获得波束赋形天线加权向量,不仅能够直接获得精确的天线加权向量,而且,相对传统的迭代方法可以大幅降低复杂度。
2 TD-LTE系统
2.1 天线配置
TD-LTE系统天线配置如图1所示。在该系统中,基站侧配置N根天线,具有同一时刻N发或N收的能力;终端侧配置2根天线,具有同一时刻1发或2收的能力[1]。与之对应,在一个TD-LTE的上行发送间隔,上行链路(从终端到基站的方向)为1发N收;在一个TD-LTE的下行发送间隔,下行链路(从基站到终端的方向)为N发2收。
考虑到目前下行链路8发2收的TD-LTE系统已被确定为是一种主流的用于室外覆盖的TD-LTE系统,本文重点关注基站侧配置N=8根天线的TD-LTE系统,进行与之对应的波束赋形方法性能和复杂度分析。尽管如此,本文所提的波束赋形方法以及复杂度分析可以直接推广到基站侧配置任意N≥2根天线的系统,并在N较大时获得类似结论。
2.2 帧结构
TD-LTE系统的上下行链路使用相同频率,基于所配置的帧结构采用时分双工(TDD)的方式进行复用[1]。一个TD-LTE帧结构配置例如图2所示,其中,上下行配置号为1,对应一个无线帧中的子帧类型为“DSUUDDSUUD”; 特殊子帧配置号为7,对应特殊子帧中DwPTS、GP和UpPTS 3个域的长度比例为10∶2∶2。
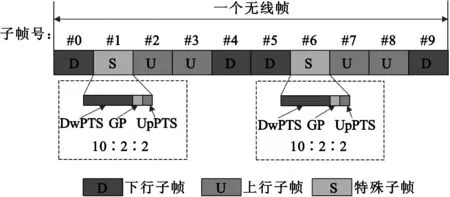
图2 一个TD-LTE帧结构配置例:上下行配置1+特殊子帧配置7
3 基于上下行信道互易性的波束赋形
TD-LTE系统属于TDD系统范畴,上下行链路使用相同频率,相对FDD系统具有天然的上下行信道互易性的特点,更便于利用上行信道的估计结果进行下行波束赋形。
特别地,在TD-LTE系统中,在上行子帧的最后一个符号或UpPTS的最后两个符号里,终端可被配置按照一定的模板发送上行SRS[1],基站可以基于终端发送的SRS估计出上行信道,并利用上下行信道的互易性,基于上行信道的估计结果计算出下行波束赋形的天线加权向量,用于波束赋形。
SRS的发送可被配置为通过终端上行固定一根天线发送(如通过终端发送天线0发送)或者终端上行两根天线交替发送(如通过终端发送天线0和1交替发送)。对于终端上行固定一根天线的SRS发送,基站基于发送的SRS可以估计出频域每个无线块(Radio Block, RB)(包含12个连续子载波,为终端进行与下行波束赋形相对应的信道估计的最小单位)上从终端SRS发送天线(如前文所提的天线0)到基站天线间的向量信道:
h0=[h0,0,h0,1,h0,2,…,h0,N-1]
(1)
式中,h0,n(n=0,1,2,…,N-1)为某RB上终端SRS发送天线与基站天线n间的信道。
基于上下行信道互易性,假设上下行信道相同,为了达到最大的相对终端SRS发送天线的波束赋形增益(即对应下行采用终端SRS发送天线进行接收时获得最大的下行发送信号接收能量的情形),对应下行波束赋形天线加权向量w(1-Ant)为
(2)
由式(2)可见,对于终端上行固定一根天线发送SRS的情形,可以容易地获得对应的下行波束赋形天线加权向量。对于一个N维的向量信道h0,计算对应的下行波束赋形天线加权向量的复杂度(表示用所需的复乘次数)仅为
O(1-Ant)=2N+1
(3)
但是,由于下行波束赋形天线加权向量仅基于部分下行信道计算得到,不能保证实际终端在下行通过两天线进行分集接收时能获得最大的波束赋形增益(或信号接收能量)。
如果终端被配置为通过上行两根天线交替地进行SRS发送,基站基于发送的SRS可以估计出频域每个RB上从终端所有两根天线(如前文所提的天线0和1)到基站天线间的完整的矩阵信道:
(4)
式中,hm,n(m=0,1;n=0,1,2,…,N-1)为某RB上终端天线m与基站天线n间的信道。基于上下行信道互易性,假设上下行信道相同,为了达到最大的终端进行两天线分集接收时的波束赋形增益(或信号接收能量),对应下行波束赋形天线加权向量w(2-Ant)应满足:
(5)
由式(5)可见,对于UE上行两根天线交替发送SRS的情形,对应的下行波束赋形天线加权向量为所获得的N×N维信道相关矩阵R=HHH的主特征向量(即对矩阵进行特征值分解后,与矩阵最大特征值相对应的特征向量,或有多个相等的最大特征值时对应特征向量的线性组合),或者等效地,为所获得的矩阵信道H的主右奇异向量(对矩阵进行奇异值分解后,与矩阵最大奇异值相对应的右奇异向量)。
4 传统的基于矩阵信道的波束赋形方法及其分析
传统地,在工程上常采用如下的迭代方法获得对应矩阵信道H的波束赋形天线加权向量w(2-Ant),即式(5)的解。
输入:
M×N维矩阵信道H
输出:
对应H的N维波束赋形天线加权向量W(2-Ant)
过程:
(1)计算N×N维信道相关矩阵R
R=HHH
(6)
(2)迭代获取C的主特征向量W(2-Ant)
1)初始化
N维初始迭代向量e0=einit
(7)
2)迭代:i=1,2,3,…,Nitr
ei=Rei-1
(8)
3)输出
W(2-Ant)=eNitr/‖eNitr‖
(9)
上述迭代方法是一种通用方法,可应用于任意M×N维矩阵信道H,未针对终端仅配置2根天线的TD-LTE系统情形(即2×N维矩阵信道H)进行特别的优化。
对TD-LTE系统中基于矩阵信道的波束赋形,基站可获得的矩阵信道H为2×N维,如式(4)所示。对应地,如采用上述迭代方法获得波束赋形天线加权向量,可将式(6)的信道相关矩阵R表示为如下的特征值分解后的形式:
(10)
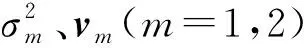
(11)
式中,主特征向量v1方向上的能量和次特征向量v2方向上的能量之比为
(12)
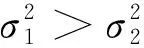
(2)当einit选取得当时,为了获得逼近期望的加权向量,也常需要进行多次迭代,复杂度较大。
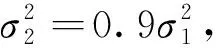
对所关注的2×N维矩阵信道H情形,式(6)、式(8)和式(9)的复杂度(表示用所需的复乘次数)分别为N2+N、N2和2N+1,如进行Nitr次迭代,总共所需的复杂度为
(13)
对于8发2收TD-LTE系统中基于矩阵信道的波束赋形,如迭代次数Nitr=20,复杂度为1 369次复乘。
5 新的基于奇异值分解的高效波束赋形方法
针对传统的基于矩阵信道的迭代波束赋形方法复杂度较大且可能不收敛的问题,本节提出一种基于奇异值分解的高效波束赋形方法。该方法利用系统终端侧仅有2根天线的系统特性,采用有针对性的基于2×2矩阵特征值分解公式的矩阵信道奇异值分解,能够直接获得精确的波束赋形天线加权向量,而且,相对于传统的迭代方法可大幅降低复杂度。
如前所述,基于矩阵信道H的波束赋形天线加权向量w(2-Ant),即式(5)的解,等效地也为矩阵信道H的主右奇异向量;因此,2×N维矩阵信道H的奇异值分解可表示为

(14)
式中,U和V分别为2×2和N×N的酉阵,Λ为2×2的对角阵,v1为期望得到的对应最大奇异值σ1的右奇异向量。
考虑到TD-LTE系统终端端侧仅有2根天线,以至于H其中一维(即H的行)的维度仅为2,且2×2矩阵的特征值分解存在高效的计算公式,为了获得H的主右奇异向量v1(即对应波束赋形天线加权向量w(2-Ant)),所提方法的基本思想为:
首先,利用2×2矩阵的特征值分解公式,计算C=HHH的特征值分解输出中“必要”的部分(以便用于后续主右奇异向量v1的计算)。
2×2矩阵C的特征值分解公式如下:
C=UΣUH
(15)
其中:
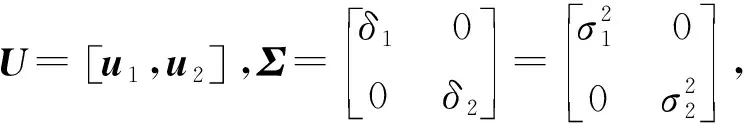
(16)
需通过2×2矩阵的特征值分解公式计算得到u1和δ1。
在本文中,利用高效的2×2矩阵ansatz特征值分解公式[6]计算特征值分解的必要输出。实际上,2×2矩阵特征值分解公式并非是唯一的。在工程实现中,也可根据特定硬件实现的方便,选择其它的2×2矩阵特征值分解公式进行计算,如Takagi 因式分解公式,本文就不再赘述。
然后,基于通过特征值分解获得的u1、δ1,以及原始的H计算得到v1。
特别地,据式(14)和式(16),可直接得到:
(17)
详细的方法计算流程如下所示,其中,sign(·)为取符号操作。
输入:
2×N维矩阵信道H
输出:
对应H的N维波束赋形天线加权向量w(2-Ant)
过程:
(1)计算2×2维信道相关矩阵C
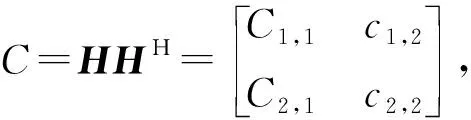
(19)
(2)利用高效的2×2矩阵ansatz特征值分解公式计算特征值分解的必要输出u1和δ1
(20)
(21)
(22)
γ1=c1,1+β,γ2=c2,2-β
(23)
如果γ1≥γ2,
u1=[s,t2s]T,δ1=γ1
(24)
否则,
u1=[-t1s,s]T,δ1=γ2
(25)
(3)基于u1、δ1,以及H计算得到H的主右奇异向量v1(即对应波束赋形天线加权向量w(2-Ant))
(26)
可见,式(19)~(24)或式(25),以及式(26)的复杂度(表示用所需的复乘次数)分别为3N、5、1、3、0、1以及2N+3,方法总共所需的复杂度为
(18)
对于8发2收TD-LTE系统中基于矩阵信道的波束赋形,复杂度为53次复乘,大大低于传统迭代方法。
6 仿真结果及分析
考虑图1所示的TD-LTE系统,基站侧配置N=8根天线,终端侧配置2根天线;帧结构配置如图2所示;信道采用3GPP定义的SCM信道模型建模[7],信道场景为城市宏小区(Urban Macro)。
图3对本文涉及的几种波束赋形方法进行了仿真性能比较。从图中可以看到,基于矩阵信道的波束赋形相对基于向量信道的波束赋形在误块率(BLER)等于0.1处具有1.5 dB的信噪比(SNR)增益。其原因在于,前者使用了完整的矩阵信道信息计算下行波束赋形天线加权向量,使得终端在两天线分集接收时,获得了最大的波束赋形增益。
从图中还可以看到,对基于矩阵信道的波束赋形,所提方法与进行了多次迭代(以使性能收敛)的传统方法相比,性能非常接近。其原因在于,所提方法通过奇异值分解可以获得精确的波束赋形天线加权向量,具有最优的性能。但是,由于所提方法是直接计算得到期望的加权向量,无需进行多次迭代,并且在计算过程中充分利用了TD-LTE系统终端侧仅有2根天线的系统特性对奇异值分解算法进行了优化,相对传统方法复杂度大幅降低。特别地,如前文分析,传统方法计算一次波束赋形加权向量需1 369次复乘;新的方法仅需53次复乘。仿真结果和复杂度分析验证了所提方法的有效性。
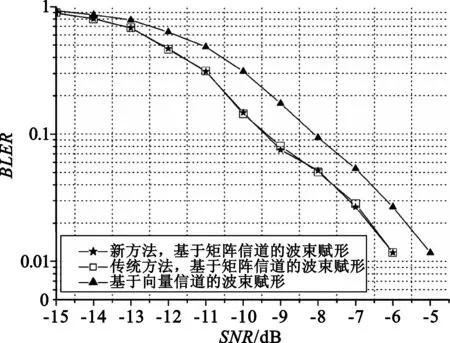
图3 波束赋形方法性能比较
7 结 论
针对TD-LTE系统中基于矩阵信道的波束赋形问题,本文提出了一种基于奇异值分解的波束赋形方法。该方法利用系统终端侧仅有2根天线的系统特性,采用基于2×2矩阵特征值分解公式的矩阵信道奇异值分解获得波束赋形天线加权向量,用于下行波束赋形。理论分析和仿真结果表明,所提方法不仅可以获得精确的波束赋形天线加权向量,具有最优的性能,而且,相对传统基于迭代波束赋形方法在相当程度上降低了复杂度,是一种在工程上既有效又实用的波束赋形方法。
参考文献:
[1] 3GPP.TS 36.211 V8.9.0,Physical Channels and Modulation[S].
[2] 2010ZX03002-002,TD-LTE面向商用基站研发[S].
2010ZX03002-002,TD-LTE commercial eNodeB R&D [S].(in Chinese)
[3] Thomas T A, Mondai B, Vook F W. Methods for Switching Between Long Term and Short Term Transmit Beamforming in OFDM[C]//Proceedings of VTC′2007-Spring.Dublin,Ireland:IEEE,2007:574-578.
[4] 李亚麟,樊迅,胡波,等.天线校准误差建模即对开环波束赋形技术的影响[J].电讯技术,2010,50(3):45-48.
LI Ya-lin,FAN Xun, HU Bo, et al. Modeling of Antenna Calibration Error and its Impact on Open-Loop Beam forming [J]. Telecommunication Engineering, 2010,50 (3):45-48.(in Chinese)
[5] Todd K M, Wynn C S. Mathematical Methods and Algorithms for Signal Processing [M].London:Prentice Hall,1999.
[6] Thomas H. Routines for the diagonalization of complex matrices [M].Germany:[s.n.],2006.
[7] 3GPP.TR 25.996 V9.0.0,Spacial Channel Model for Multiple Input Multiple Output (MIMO) Simulations [S].

