STFT算法在短波差分跳频信号检测中的应用*

(武汉工程大学 电气信息学院，武汉 430073)

1 引 言

与传统的短波跳频体制相比，差分跳频(Differential Frequency Hopping,DFH)技术[1]将编码、调制和跳频结合在一起，利用相邻跳频频率的相关性携带信息，提高系统的抗干扰能力。DFH系统的跳速高达5 000跳/秒，短波信道对DFH信号和传统低速跳频信号的影响是不同的，文献[2]提出了基于短时傅里叶交换(Short Time Fourier Transformation，STFT)与G函数相结合的跳检测方法，但仅开展了检测研究，没有进行性能分析；文献[3]利用四阶累积量研究了高斯噪声下基于ARMA建模法的DFH信号频率检测，仅选择了高斯噪声信道；而文献[4]通过提取小波脊进行时频分析和参数估计的信号检测，但其运算量稍大；文献[5]则重点计算并分析了利用不同窗口函数跟踪跳频信号时的性能；文献[6]研究了基于卷积码模型的维特比硬判决和维特比软判决两种最大似然检测算法, 并对在信道下的两种最大似然检测算法的性能进行研究。本文分析了短波信道对DFH信号的影响，基于Turbo码的G函数模型，采用基于STFT和最大后验概率(MAP)译码算法相结合的跳检测方法，并进行了数值仿真。

2 短波差分跳频系统模型

短波差分跳频系统的结构如图1所示。G函数为频率转移函数，若给定输入数据XN和上一跳的频率FN-1，则当前跳的频率FN=G(FN-1，XN)是输入数据XN和上一跳频率FN-1的函数。本文采用基于符号的Turbo编码[7-9]实现G函数，采用MAP译码算法[7-10]实现逆G函数。

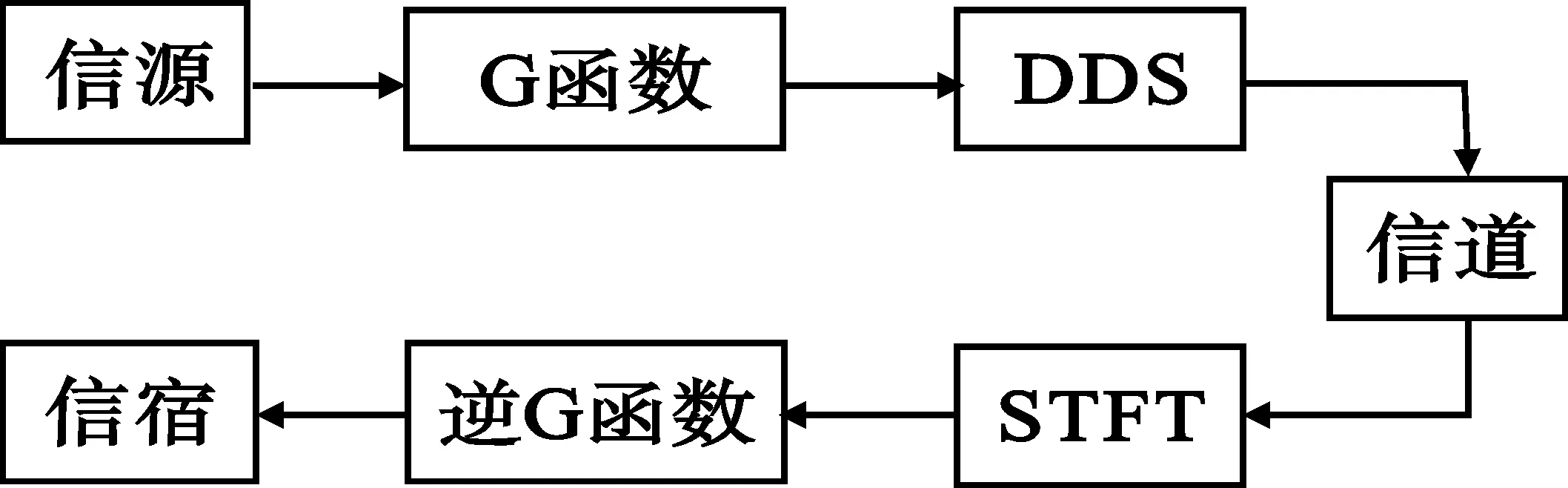
图1 短波DFH系统模型

在发射端，Turbo编码器采用两个基于符号的递归系统卷积码器并联而成，并在编码器后附加一个信道交织器，其目的是将突发错误离散成随机错误。然后，根据符号的十进制值直接进行射频频率映射，为了减小邻近频道干扰，结合脉冲赋形技术，采用直接数字合成(DDS)射频信号。接收端对接收到的跳频信号利用STFT算法进行解跳，得到各跳频频率的能量值，解交织后利用MAP算法进行逐符号译码，最后得到输出信息。本文所研究的系统指标如下：数据速率为9.6 kbit/s，跳速为5 000跳/秒，数据的帧速率为20帧/秒；每帧数据包含250跳，其中240跳用于传输数据，10跳用于信道探测和同步；系统总带宽为80 kHz，频率集包含16个频点。

3 短波信道对DFH信号的影响

短波电离层反射信道是一种时变色散信道，多径效应、群时延和多普勒效应是其主要特点。短波电离层传播的多径效应引起的信道时间色散，造成信道的频率选择性衰落，由相干带宽表征；电离层的多普勒效应引起的信道频率色散，造成时间选择性衰落，由相干时间表征[11-12]。信号的持续时间和带宽不同，短波信道对信号的影响也不相同。

3.1 多径效应对DFH信号的影响

短波信道多径时延95%都集中在0.5～4.5 ms之间[12]，在传统低速跳频系统中，信号驻留时间长，多径效应对本跳信号造成影响，使其幅度呈现瑞利衰落。然而，DFH系统的跳速高达5 000跳/秒，每跳驻留时间只有200 μs，因此本跳信号幅度基本不受多径影响。

然而，跳信号经过多径时延后虽然不会出现在本跳驻留时间内，仍然会对其后的几跳信号造成干扰，导致一跳信号内存在多个频率的干扰信号[12]。因此，可以将短波信道多径效应对DFH信号的影响看作是一种多频干扰。

3.2 群时延对DFH信号的影响

在短波信道中，沿同一路径传播的异频信号具有不同的传播速度，用群时延来表示相关跳频信号沿同一天波路径的传播时延。群时延造成相邻跳信号之间间隔不再等于一跳的时长，引起跳频信号的畸变[10]。研究表明，短波信道的群时延为每兆赫几十微秒[12]，与DFH信号驻留时间相当。群时延使相邻跳信号发生了部分重叠，若重叠达到跳频脉冲宽度的一半以上，系统将无法区分信号，造成通信中断。因此对高速跳频系统而言，群时延会对系统性能造成严重影响。

3.3 多普勒效应对DFH信号的影响

短波信道相干时间约为1～10 s[12]，DFH信号每跳时长约为200 μs，远远小于信道相干时间，因此可以近似地认为信道是一个慢衰落信道，在一跳驻留时间内，信道的衰减和相移特性是非时变的。

综上所述，短波信道对DFH信号的影响与对传统低速跳频信号的影响是不同的。因此，本文将短波信道建模为加入群时延和多径干扰的加性高斯白噪声信道。

4 跳频信号的跳检测

根据上述关于短波信道对DFH信号影响的分析可知，由于短波信道的多径和群时延效应，任一跳频间隔内的频率信号受到多个频率成分的干扰。

短时傅里叶变换是一种时频分析方法，通过对信号加窗来分析信号在特定时间间隔内的频谱特性，因而可以用来分析一跳时间间隔内信号的频率特性。研究表明，高斯(Gauss)窗函数的时间-频率积满足H不等式下限，具有最好的时间、频率分辨率[11]，而且具有加强中心附近的信号以及抑制远离其中心位置信号的特点，对信号加窗后，可以抑制群时延造成的邻近跳信号频率以及多径造成的其它干扰频率，降低这些信号的幅度。因此，采用高斯窗对跳信号进行STFT分析可以在一定程度上减少短波信道的不利影响。为了便于计算机实现，通常采用STFT的离散形式(DSTFT)。设抽样间隔为TS，记x(n)=x(nTS)，可得到DSTFT形式如下：

式中，N为在时间轴上窗函数移动的步长，g(n)为离散形式的高斯窗函数。

本文G函数采用基于符号的Turbo编码方法实现，逆G函数采用MAP译码算法。文献[7]研究表明，MAP算法是实现Turbo迭代译码最好的次最优算法。本文采用STFT与MAP译码算法相结合的跳频信号频率检测方法。

在接收端进行逐符号MAP译码实现逆G函数时，关键是确定网络图中分支转移概率值，根据文献[10]关于M元正交信号错误概率的相关理论可知，这些频点的能量值服从某些特定的分布。为确定该值，首先要得到由各频率能量值构成的某时刻能量矢量Et=(Et,0,Et,1,…,Et,M-1)，从而确定发送各频率的概率，再结合其它相关信息确定分支转移概率。

本文采用的跳频检测方法如下[11-12]：假定系统已同步，对接收到的当前跳信号作STFT，其窗函数采用高斯窗，而时间中心对应于当前跳信号的中心，然后将所得到的能量矢量送入MAP译码单元进行逐符号译码，然后移动窗函数对准下一跳信号中心，继续下一跳信号的跳检测。

5 仿真及结果分析

本文在VC++6.0编程环境下对STFT和MAP译码相结合的跳检测方法进行了数值仿真，分别验证了该方法在高斯信道和等效短波信道下的检测性能，并对分别存在多径干扰、群时延和多普勒效应的情况进行了仿真。

为了便于仿真，本文只考虑接收端经过下变频后的基带信号，并采用归一化解频率。接收信号经过采样后，每跳信号包含N=32个点。同时，高斯窗函数取归一化幅度值，窗长也相应选取为32个点。基于符号的Turbo编码器选取的RSC分量码生成多项为(51，77)8，采用交织长度为240且满足S距离的模K交织器。仿真时，信道的群时延和多径时延时间均随机产生，其范围分别控制在0～100 μs和0.5～3 ms。

图2是在AWGN下仿真所得跳频检测性能曲线，图中4条曲线分别代表MAP译码的迭代次数分别取1、2、4、8时的情况。如图所示，MAP译码算法的迭代次数对译码性能有重要影响，随着迭代次数的增加，误码率明显减少，当信噪比为0.2 dB时,其误码率可达到10-5。

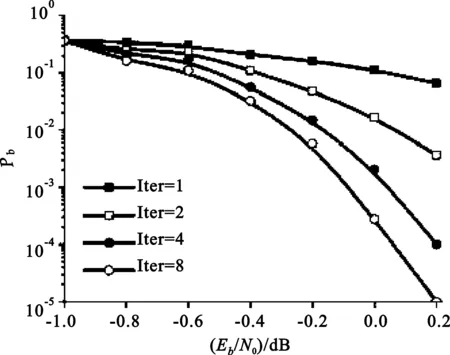
图2 AWGN信道下跳频信号检测性能

图3为考虑信道存在多径干扰情况时的跳检测性能曲线，仿真的多径传播路径数目分别取为2条和3条，当信噪比达到6 dB时，误码率降到10-5，可见多径干扰对DFH信号的跳检测存在不利的影响。

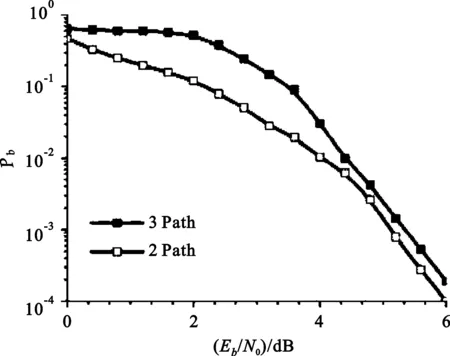
图3 多径干扰时的跳信号检测性能

图4为是考虑信道存在群时延情况时的跳检测性能曲线，当信噪比达到1.6 dB时，采用8次迭代，系统误码率可降低到10-6。

图5是考虑多普勒效应后跳检测性能曲线，与图5比较后可见，加入多普勒效应后，误码性能变化很小，仿真结果与上述关于短波信道对高速跳频信号影响的分析一致。

图6为综合考虑了多径干扰和群时延情况后的系统性能曲线，MAP译码算法迭代次数为1、2、4和8。由于同时考虑了多径和群时延的干扰，信噪比达到约6.8 dB时，迭代8次可使误码率降到10-5。

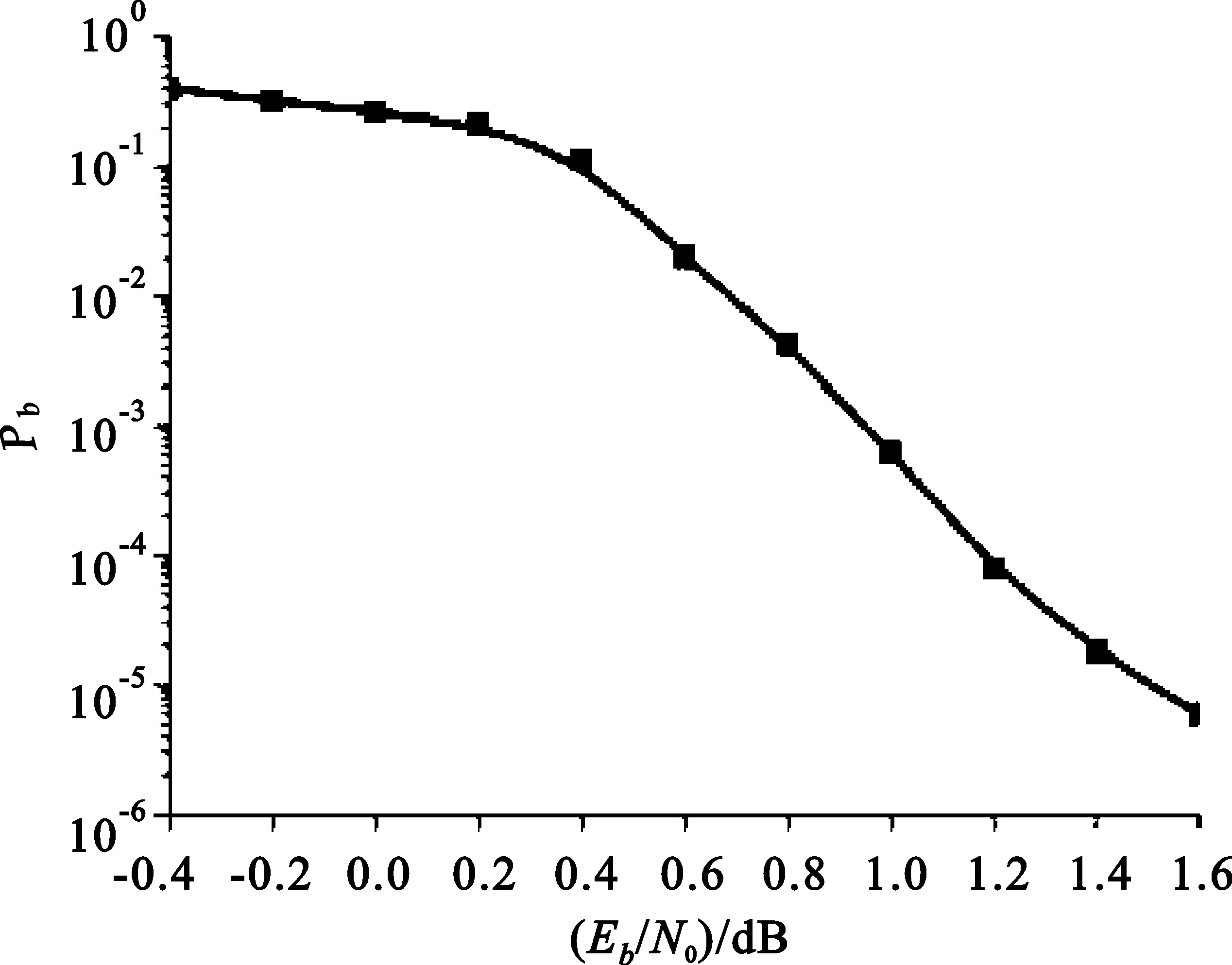
图4 存在群时延时的跳检测性能

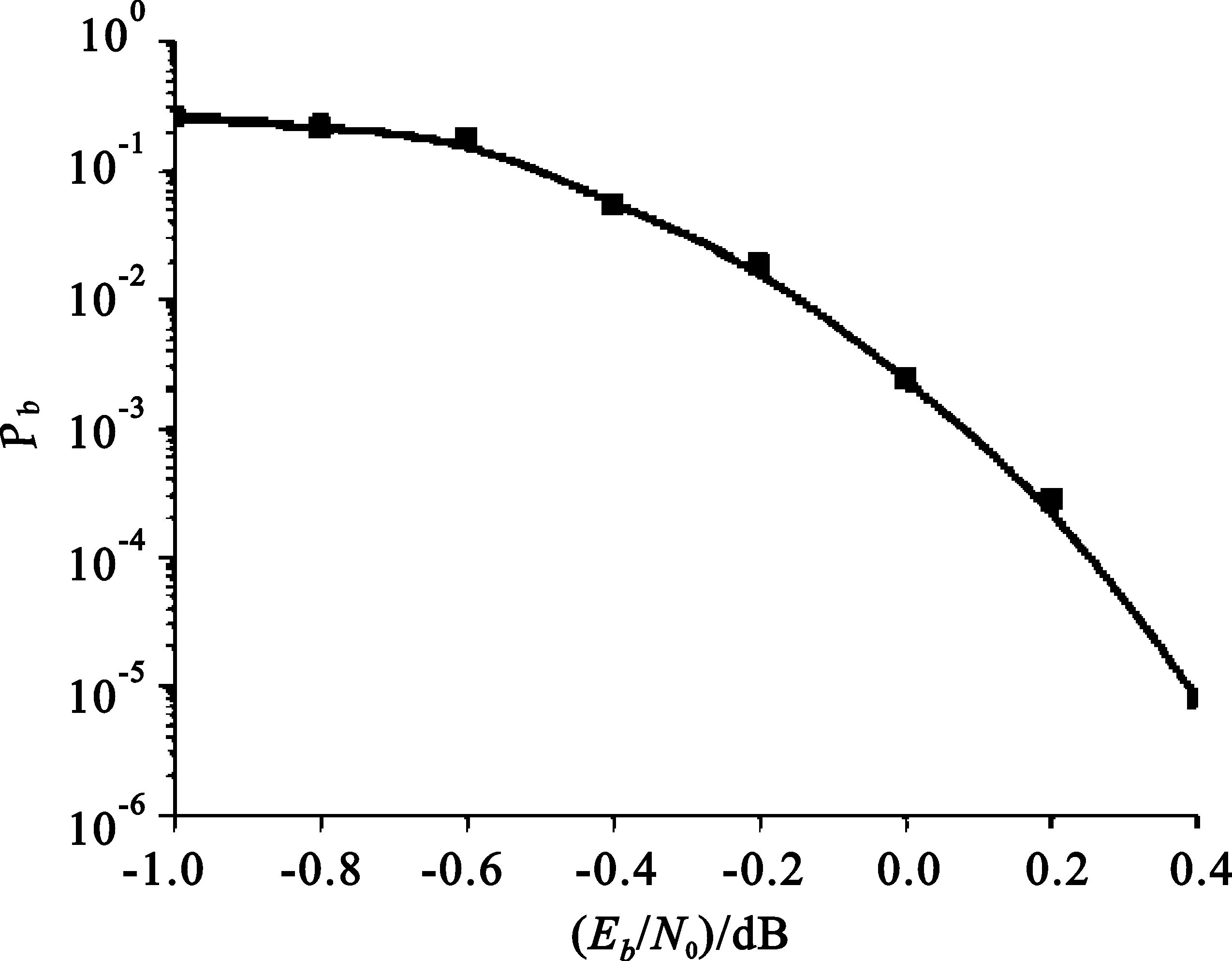
图5 存在多普勒效应时的跳检测性能

仿真结果表明，短波信道的多径干扰和群时延对高速跳频信号存在重要影响，利用STFT和MAP译码算法对DFH信号进行跳检测可以得到较好的抗干扰性能。而且，STFT可看作是加窗处理的傅里叶变换，因此也可采用快速算法，实现方法简便，特别适合DFH信号的检测。

6 结束语

跳频信号检测是差分跳频技术的关键部分，跳检测方法的性能对于DFH 系统至关重要。本文首先分析了短波信道对DFH信号的影响，然后采用STFT与MAP译码算法相结合的方法对跳频信号进行检测。理论分析和仿真结果表明，短波信道多径干扰会对DFH信号造成多径干扰，其影响可看作是一种多频干扰；群时延会造成相邻跳DFH信号重叠，影响系统性能；而多普勒效应对信号的影响较小。与文献[6]相比，基于Turbo码建立的G函数模型，采用该方法进行跳频信号检测，在综合考虑短波信道影响后，信噪比为6.8 dB时，误码率可达到10-5，可实现对DFH信号的有效检测，其性能远优于基于卷积码的G函数模型。

参考文献：

[1] Herrick D L, Lee P K.CHESS:A new reliable high speed HF radio[C]//Proceedings of Military Communications Conference.McLean, VA USA:[s.n.],1996:684-690.

[2] 刘忠英,张毅,姚富强.基于STFT与G函数相结合的短波DFH跳检测方法[J].电子学报，2003 31(1):13-16.

LIU Zhong-ying,ZHANG Yi,YAO Fu-qiang.HF DFH HOP-Detecting Method Based on STFT and G Function[J].ACTA Electronic Sinica,2003,31(1):13-16.(in Chinese)

[3] 隋丹,葛临东.高斯噪声下差分跳频信号的高分辨率频率检测[J].电讯技术,2005, 45(4):79-82.

SUI Dan,GE Lin-dong. High Resolution Frequency Estimation of Differential Frequency Hopping Signal in Gaussian Noise [J]. Telecommunication Engineeering, 2005,45(4):79-82.(in Chinese)

[4] 王明海,苟彦新,田岩.一种基于小波脊时频分析的差分跳频信号检测方法[J].电讯技术,2008,48(3):86-90.

WANG Ming-hai,GOU Yan-xin,TIAN Yan. A Differential Frequency Hopping (DFH) Signal Detection Method Based on Wavelet Transform and Time-frequency Analysis[J]. Telecommunication Engineeering, 2008,48(3):86-90.(in Chinese)

[5] 许红军,柯建波,党百振.跳频信号的STFT时-频分析[J].桂林电子工业学院学报,1998 18(1):15-19.

XU Hong-jun,KE Jian-bo,DANG Bai-zhen.The STFT Time-frequency Analysis of FH-SS Signal[J].Journal of Guilin Institute of Electronic Technology, 1998,18(1):15-19.(in Chinese)

[6] 董彬虹,李少谦,陈智,等.差分跳频信号最佳接收机设计[J].电子科技大学学报,2003，32(5):530-534.

DONG Bin-hong,LI Shao-qian,CHEN Zhi,et al. Design of Optium Receiver for DFH signal[J].Journal of University of Science and Technology of China,2003,32(5):530-534.(in Chinese)

[7] 刘东华.Turbo码原理与应用技术[M].北京:电子工业出版社,2004:72-98.

LIU Dong-hua.Principle and Application of Turbo Code[M].Beijing：Publishing House of Electrnics Industry，2004：72-98.(in Chinese)

[8] Bingeman M,Khandani A K. Symbol -based Turbo Codes[J].Communications Letters,1999 3(10) :285-288.

[9] J Yuan, W Feng, B Vucetic.Turbo trellis coded modulation for fading channels[C]//Proceedings of IEEE Vehicular Tecnology Conference.[S.l.]:IEEE,2000:2059-2063.

[10] John G Proakis.Digital communications [M]. 4th ed.USA：McGRaw-Hill Companies,Inc,2000: 814-887.

[11] 王亚军,张玉,解明祥.短波电离层反射信道模型的建立与仿真[J].电波科学学报,2004，19(3):357-361.

WANG Ya-ium,ZHANG Yu,XU Ming-xiang. Model ing and simulation of short-wave ionospheric radio channel[J].Chinese Journal of Rradio Science,2004 19(3):357-361.(in Chinese)

[12] 胡中豫.现代短波通信[M].北京:国防工业出版社,2003:91-98.

HU Zhong-yu.Modern Short-wave Communication[M].Beijing:National Defense Industry Press,2003:91-98.(in Chinese)