基于相干对消的噪声子空间自适应估计
李 涛,李国林2,廖辉荣
(1.海军航空工程学院 研究生管理大队,山东 烟台 264001;2.海军航空工程学院 七系,山东 烟台 264001)
1 引 言
多重信号分类(MUSIC) DOA估计算法作为主流的超分辨算法之一,自出现以来就一直受到关注,由于其运算量较大,关于降低其运算量的研究也一直在进行。MUSIC算法的运算量主要集中在特征值分解和空间谱的搜索两部分,目前已有的研究也主要集中在这两方面。采用自适应算法来估计子空间的方法能够减少计算量且适合子空间的更新,Oja[1]提出了基于阵列输出数据的协方差矩阵构建代价函数,并采用梯度算法递归估计子空间;SarkarT[2]对其进行改进,即采用梯度的瞬时估计来代替基于协方差矩阵代价函数的梯度,得到最小均方(LMS)型梯度的估计子空间,但在每一步参数矢量更新时需要对参数矢量进行归一化处理,引入了多个乘法和除法运算,造成实时计算的瓶颈;Lei Xu[3]对归一化过程进行改进,简化了运算。上述方法均从代价函数的最小化设计自适应过程,得到的运算量约为O(M2N),文献[4-9]则分别利用接收数据近似、阵元降维,以及基于Householoder压缩理论等方法研究了信号子空间或噪声子空间的快速估计算法,避开了特征值分解问题或简化了运算,得到的运算量约为O(MN);文献[10-13]分别利用FFT、阵元降维和有限域搜索等方法研究了空间谱的快速搜索问题。这些方法不同程度地降低了MUSIC算法的运算量,但同时多数存在估计精度降低的问题。本文从相干信号的自适应对消的角度考虑噪声子空间的估计问题,得到基于阵列输出自适应对消的噪声子空间估计算法。
2 信号模型与MUSIC算法

图1 均匀线性阵列Fig.1 Uniformlinear array
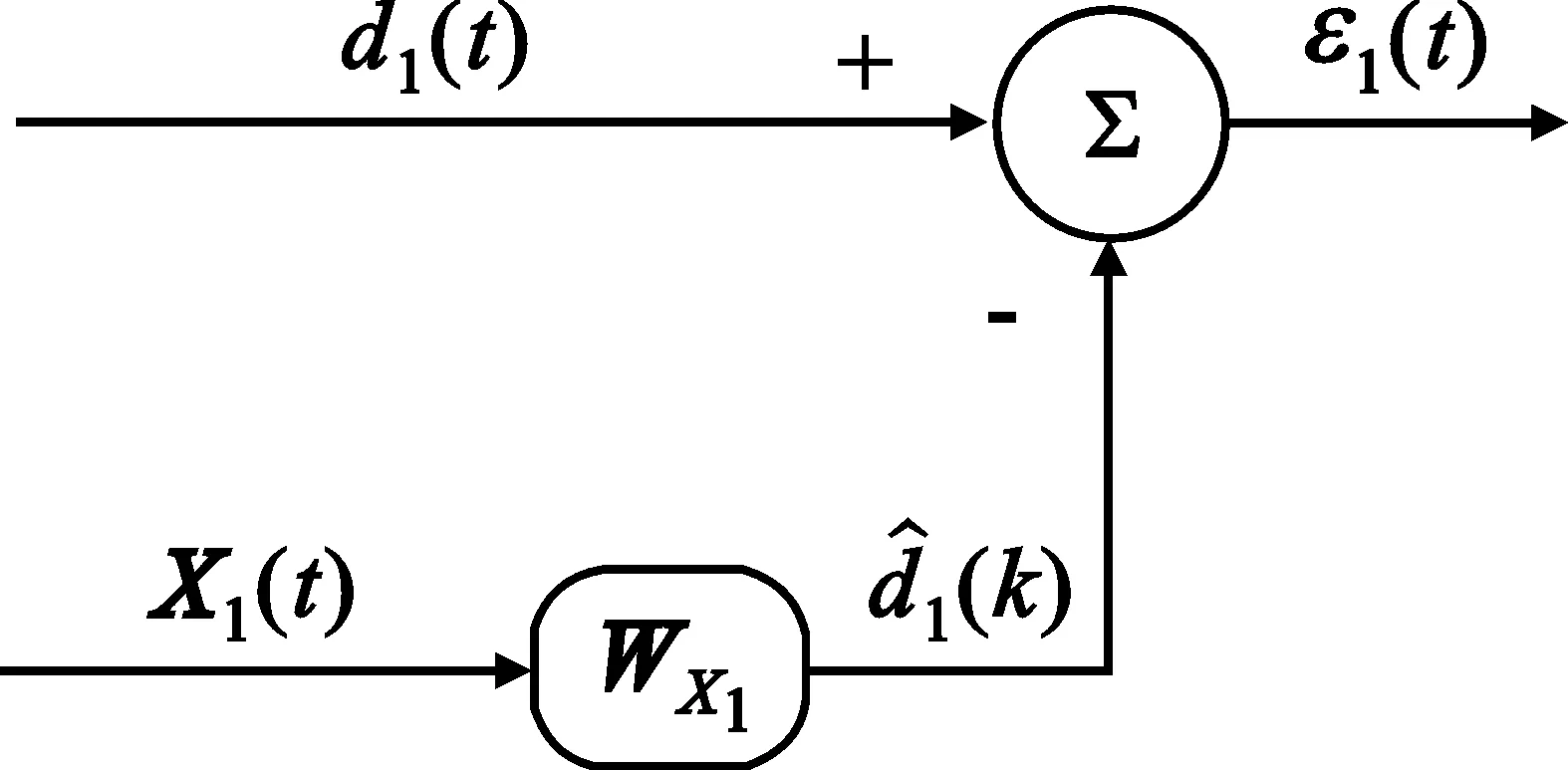
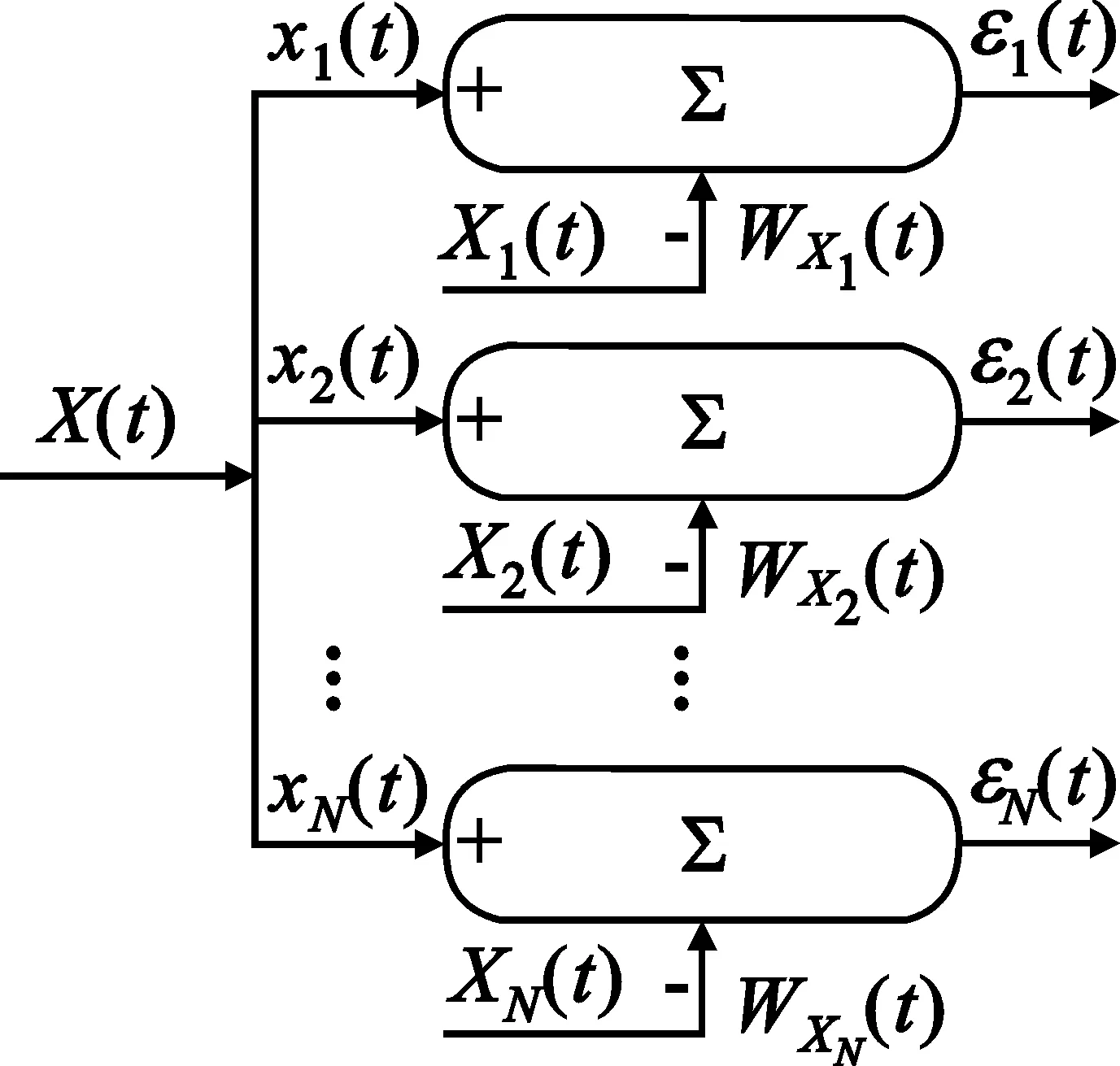
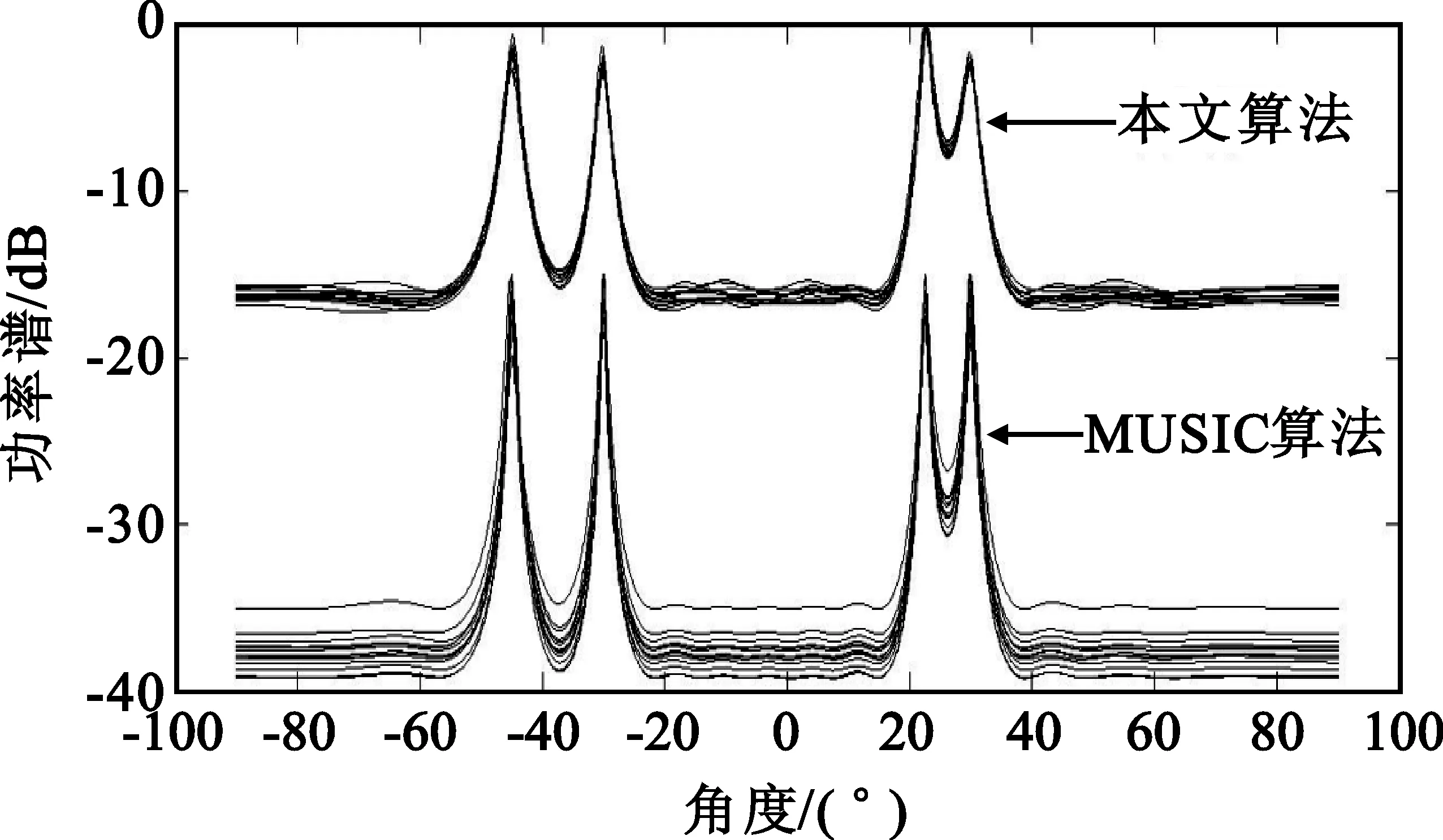
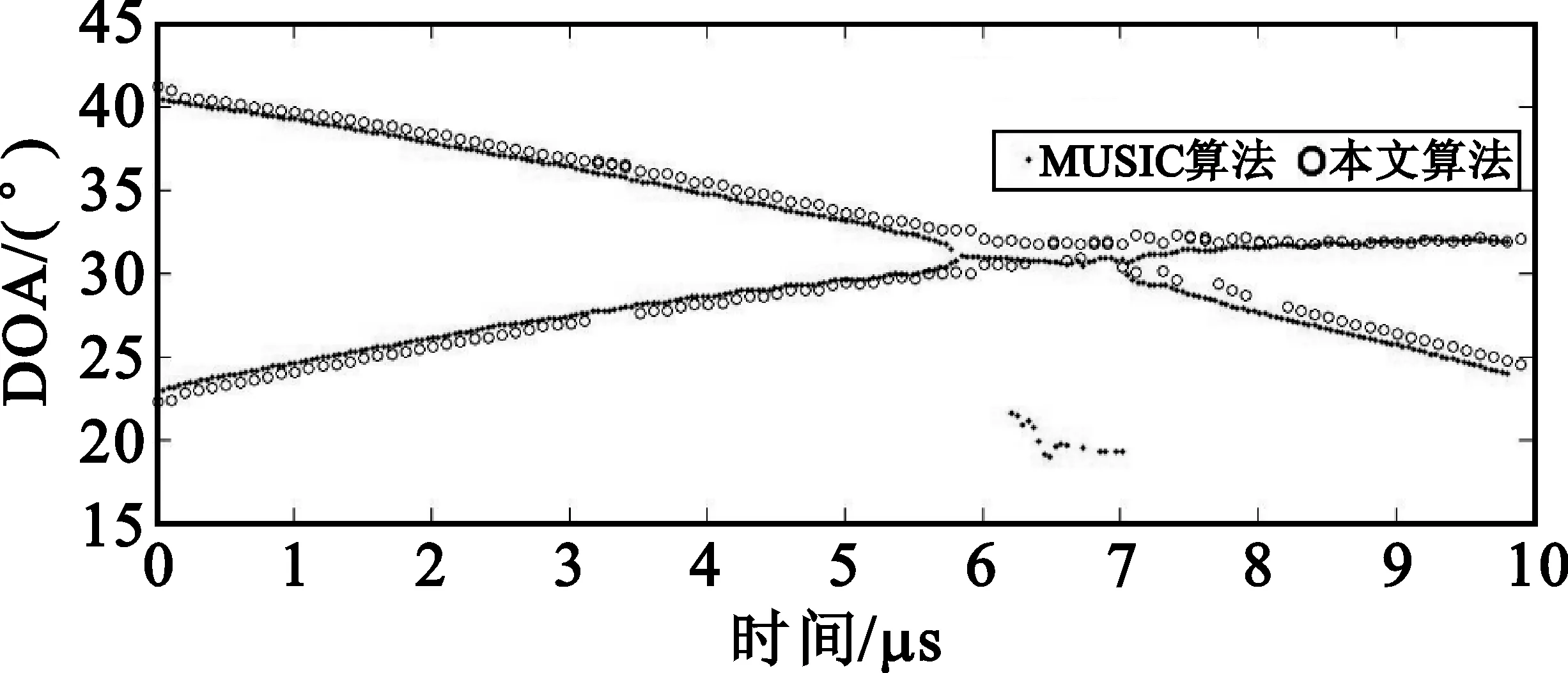
考虑一个由N个全向阵元组成的均匀线性阵列,阵列间距为d,如图1所示。假设M个远场窄带信号(M (1) 式中,si(t)为第i个信号,λi为其中心波长,nk(t)为第k个阵元中的零均值高斯加性白噪声。则阵列的输出信号矢量可表示为 X(t)=[x1(t),x2(t),x3(t),…,xN(t)]T= A(θ)S(t)+N(t) (2) 其中: A(θ)=[a(θ1),a(θ2),…,a(θM)] (3) 为N×M维阵列流形矩阵,a(θi)为对应的方向向量,且有: (4) S(t)=[s1(t),s2(t),s3(t),…,sM(t)]T (5) 为M个入射信号矢量。 N(t)=[n1(t),n2(t),n3(t),…,nN(t)]T (6) 为阵列噪声矢量,且满足: E[N(t)NH(t)]=σ2I (7) 由式(2),阵列输出信号自相关阵为 R=E[X(t)XH(t)]=A(θ)RsAH(θ)+σ2I (8) 其中: RS=E[S(t)SH(t)] (9) 当信号不相关时,RS为满秩的M维对角阵。 对R进行特征分解,由R的M个大特征值对应的特征向量E张成M维信号子空间,而R的N-M个小特征值对应的特征向量U张成N-M维噪声子空间,由于: span[A(θ)]=span[E] (10) 因而U⊥span[A(θ)],进而U⊥a(θi)。采用MUSIC算法来估计信号DOA,空间谱为[14] (11) 式中,U为噪声子空间矩阵,a(θ)为方向向量。 由此我们发现MUSIC算法是由U⊥a(θi)这一本质特征来搜索空间谱的,因此对式(2)左边乘UH可得: UHX(t)=UHA(θ)S(t)+UHN(t)=UHN(t) (12) 式(12)的结果是N-M个纯噪声信号,且由于U的列相互正交,结果是N-M个正交的噪声信号。 噪声子空间估计的问题是怎么求取U,由矩阵分解得到的噪声子空间矩阵U为噪声子空间的一个完备正交基底,事实上噪声子空间的估计并不需要得到完备的正交基底,一组完备的互不相关的基底也能满足要求。由式(12)可发现,用U的列向量对阵列输出进行加权求和,结果不含任何信号分量,换句话说,如果一个列向量对阵列输出进行加权求和,结果不含任何信号分量,则此列向量必定位于噪声子空间。从这个角度出发,如果将阵列输出进行相互的自适应对消,则由于各个阵元的输出中信号之间是相干的,输出将能够完全对消,下面将证明这一点在信号源数目少于阵元数目是能够保证的。为此首先我们看图2的维纳滤波器用于干扰对消的原理。 图2 维纳滤波器用于干扰对消原理Fig.2 Principle of Winner filter for coherent signal cancellation (13) 式中,RX1为X1(t)的自相关阵,rX1d1为X1(t)与d1(t)的互关。X1(t)能够对消d1(t)中与之相关的信号,输出ε1(t)是d1(t)中与X1(t)不相关的期望信号。如果d1(t)中存在M个不相关的干扰,则WX1向量维数必须大于或等于M才能实现干扰的完全对消。 考虑阵列输出的信号分量A(θ)S(t),以第一个阵元作为维纳对消器的参考信号为例,则: d1(t)=[1…1]S(t)+n1(t) (14) X1(t)=A′(θ)S(t)+N′(t) (15) 式中,A′(θ)为A(θ)除去第一行后的矩阵,N′(t)为N(t)除去第一个元素后的向量。由于噪声为互不相关的,因此无法对消。由式(14)、式(15)知: [1…1]S(t)=[1…1](A′HA′)-1A′HX0(t)= bX1(t) (16) 式中: b=[1…1](A′HA′)-1A′H (17) 当A′(θ)列满秩,即信号源个数小于阵元个数时式(17)存在唯一确定解。式(16)表明,d1(t)与X1(t)中的信号完全相干,因此在满足式(17)有解的条件下将能实现完全对消,即: [1 -b]A(θ)S(t)=0 (18) 由于S(t)中时间标量的任意性,必有: [1 -b]A(θ)=0T (19) 由式(19)知行向量[1 -b]必定位于噪声子空间。如果对阵列的各个阵元均进行对消,如图3所示,得到的N个行向量则张成整个噪声子空间。 图3 阵列输出相干对消原理Fig.3 Principle of coherent array output signals cancellation 图3中Xi(t)为阵列输出除去第i个阵元的输出后构成的阵列输出向量。 行向量[1 -bi]的求解有赖于式(13)的求解,对式(13)采用自适应算法求解则可得到噪声子空间的自适应求解算法。我们以LMS算法为例来说明,易知求解式(13)的LMS算法权值更新方程为 WXi(t+1)=WXi(t)+μxi(t)εi(t) (20) 式中,μ为自适应步长,定义由WXi(k)生成的对角元素为零矩阵 (21) 式中省略了时间标量,且W的第个i行向量的非零元素对应于用于对第i个阵元进行对消的权矢量WXi(t),则: ε(t+1)=X(t)-W(t)X(t) (22) 式中,ε(t+1)为阵列输出对消后的误差向量,式(20)的系数更新过程的矩阵形式为 W(t+1)=W(t)+2με(t)XH(t) (23) 其中对角元素不予计算,且设为0。由W构造矩阵 (24) 理想情况D的各行将最终收敛于行向量[1 -bi]构成的矩阵,即噪声子空间。 由于D的N×N维矩阵,当已知信号个数时,式(22)的迭代过程可以只限于W的前M列,M为信号个数。式(22)和式(23)一次迭代过程需要的计算量为2(N-1)M次乘法和2(N-1)M次加法运算,运算量为O[(N-1)M]。将D代替式(11)中的U,则可以进行空间谱估计。当信号个数未知时,由于D为N×N矩阵,搜索过程较之式(11)运算量变大,尤其是当信号源数较多时,此时可以对搜索过程进行一定的优化,例如利用D的第一行与a(θ)的乘积估计功率谱,保存功率谱峰值,再通过D的其它行来对第一步的峰值进行验证,采用这种方法将大大降低搜索的计算量。总结基于相干对消的噪声子空间估计算法如下(基于LMS算法): (1)设置初始系数矩阵W为全零矩阵; (2)由式(22)计算ε(t); (3)由式(23)更新系数矩阵W; (4)计算ε(t)功率,判断W是否收敛,当收敛时进入第5步的搜索过程,否则转入第2步; (5)设计搜索步长Δθ,由式(24)根据W构建D; (6)由D的第一行搜索功率谱,存储峰值位置; (7)由D的其它行验证存储峰值,保留对于D所有行均形成峰值的位置作为最终的搜索结果。 如果对DOA进行连续跟踪,只需对W根据式(23)进行连续更新,并进行连续空间谱搜索即可。 仿真试验验证算法4个方面的性能,试验1验证算法对信号DOA估计的准确性,试验2验证算法在不同信噪比条件下的DOA估计性能,试验3验证算法对信号DOA估计的分辨力,试验4验证算法的DOA跟踪性能,均通过与MUSIC算法的比较来验证。 (1)试验1:DOA估计 设阵元个数为16,阵元间距d=λ/2,λ为信号波长。信号采样率为2.5 GHz,信号载频为500 MHz。4个等功率窄带信号分别从-45°、-30°、30°和22.5° 4个方向入射到阵列,图4(a)给出了信噪比为10 dB的仿真结果,图4(b)给出了信噪比为0 dB的仿真结果,仿真采用256次快拍,μ=0.001。 图4共进行30次蒙特卡罗仿真,为便于观察对MUSIC算法的结果分别下移了30 dB和15 dB。结果显示在10 dB信噪比条件下本文算法能够很好逼近MUSIC算法性能,信噪比为0 dB时,算法性能较之MUSIC算法下降,但依然保持良好的高分辨率性能。 (a)信噪比为10 dB的结果 (b)信噪比为0 dB 的结果图4 DOA估计的蒙特卡罗仿真结果Fig.4 Simulation results of DOA estimation by Monte Carlo (2)试验2:不同比信噪比条件下的DOA估计 设阵元个数为12,2个等功率窄带信号分别10°、25°方向入射到阵列,信噪比为-20~5 dB,其它参数不变,在每个信噪比条件下做200次蒙特卡罗仿真,用两个信号DOA估计方差的平均作为最终的方差估计,图5给出了不同信噪比时的DOA估计方差。 图5 不同信噪比的DOA估计均方差Fig.5 RMSE of DOA estimation by different SNR 图5的结果显示,在低信噪比的情形下,采用本文算法估计的DOA的方差略大于MUSIC算法,这主要是因为LMS算法是一种次优估计技术,存在固有的估计误差,即额外最小均方误差(MSE)。 (3)试验3:DOA估计的分辨力 设阵元个数为12,2个等功率窄带信号分别从20°-Δθ和20°+Δθ方向入射到阵列,Δθ取0.2°到6°范围,步进为0.2°,信噪比为5 dB,其它参数不变,对每个Δθ采用128次快拍做200次蒙特卡罗仿真,以能够分辨两个信号DOA为成功标准,图6给出了不同Δθ时的成功率。图6的结果显示采用本文算法估计的DOA的分辨力略小于MUSIC算法,同样是因为固有估计误差的结果。 图6 角度分辨力Fig.6 Discrimination performance (4)试验4:DOA跟踪性能 (25) 图7 DOA跟踪性能Fig.7 Performance of DOA Tracking 图7中的两条曲线是空间谱峰值的轨迹。在信号源方向间隔较大时,算法能够起到良好的跟踪效果。其跟踪效果与基于阵列输出信号自相关阵更新的MUSIC算法效果相当。在信号源交会段DOA的轨迹出现波动甚至重叠,但依然保持良好的平滑性,较之MUSIC算法不会出现错误的跟踪结果,这主要归功于基于LMS系数矩阵W的更新是连续的,体现了式(23)连续迭代运算的优越性。 综上所述,采用阵列输出自适应对消的噪声子空间估计方法,能够在不需要进行特征分解的前提下估计噪声子空间,大大降低了计算量,且算法的计算过程适合并行计算,便于工程实现。由于自适应算法迭代计算的本质,适合用来进行噪声子空间的更新估计,对于运动信号源来说,方位的跟踪估计的计算量较之特征分解的方法降低是非常可观的。工程实用时有以下几点考虑: (1)当信号源数较少时,对消系数矩阵W可以进行简化,可以仅保留W的一定量的斜对角元素,而将其它元素设为零,这样用来对消的阵列输出减少,从而减少计算量; (2)关于阵元数。仿真过程发现,当阵元数较少时,例如8个阵元,算法性能在信号源数增加时下降较快,但当阵元数较大时,能很好逼近MUSIC算法的分辨率性能; (3)关于自适应过程。论文的仿真采用的是LMS算法,也可以采用RLS算法,可以预见RLS会有更快的收敛速度。 参考文献: [1] Erkki Oja. On Stochastic Approximation of the Eigenvectors and Eigenvalues of the Expectation of a Random Matrix[J]. Journal of Mathematic Analysis and Applications,1985,33(1):69-84. [2] Sarkar T K,Dianat S A,Chen H,et al. Adaptive Spectral Estimation by the Conjugate Gradient Method[J]. IEEE Transactions on ASSP, 1986,34(2):272-284. [3] LEI Xu, Erkki Oja, Ching Y S. Modified Hebbian Learning for Curve and Surface Fitting[J].Neural Networks,1992,5(3):441-457. [4] Gierull C H. Angle estimation for small sample size with fast eigenvector-free subspace method[J]. IEEE Proceedings-Radar Sonar Navigation,1999,146(3):126-132. [5] Mohammed A Hasan, Jawad A K Hasan. Fast algorithms for signal subspace estimation with applications to DOA estimation[C]//Proceedings of the 1999 IEEE International Symposium on Circuits and Systems.Orlando, FL, USA:IEEE,1999:223-226. [6] Mohammed A Hasan. Fast rational approximation algorithms of signal and noise[C]//Proceedings of 2001 Sixth International Symposium on Signal Processing and its Applications. Kuala Lumpur,Malaysia:IEEE,2001: 124-127. [7] Strobach Peter. The Householder compressor theorem and its application in subspace tracking[J].Signal Processing, 2009, 89(5): 857-875. [8] 黄磊,吴顺君,张林让,等.快速子空间分解方法及其维数的快速估计[J]. 电子学报,2005,33(6):977-981. HUANG Lei, WU Shun-jun, ZHANG Lin-rang,et al. A fast method for subspace decomposition and its dimension estimation[J]. ACTA ELECTRONICA SINICA,2005,33(6):977-981.(in Chinese) [9] Stoica P.Maximum-Likelihood DOA Estimation by Data-Supported Grid Search[J]. IEEE Signal Processing Letters, 1999,10(6):273-275. [10] Paine A S, Qineti Q Malvern. Fast MUSIC for large 2-D element digitized phased array radar[C]//Proceedings of the International Radar Conference.Adelaide Australia:IEEE,2003: 200-205. [11] CUI Wei-wei, CAO Zhi-gang. Fast Source Location Method Using Anti-reverberant Searching Space Pre-estimation[C]//Proceedings of 2006 IEEE Region 10 Conference(TENCON 2006). Hongkong:IEEE,2006:1-4. [12] 蒋毅,古天祥. 基于有限域搜索的MUSIC法快速频率估计[J].仪器仪表学报,2006,27(11):1526-1528. JIANG Yi, GU Tian-xiang. Quick frequencyestimation based on MUSIC algorithm[J]. Chinese Journal of Scientific Instrument, 2006,27(11):1525-1528.(in Chinese) [13] 曾浩,张迎辉,冯文江.快速子空间谱峰搜索方法[J].计算机应用,2009,29(9):2546-2547. ZENG Hao,ZHANG Ying-hui,FENG Wen-jiang.New peak searching method in subspace spectrum[J].Journal of Computer Applications,2009,29(9):2564-2547.(in Chinese) [14] Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986,34(3):276-280.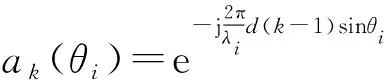
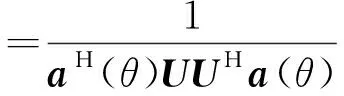
3 基于相干对消的噪声子空间估计

4 仿真试验及结果分析



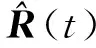
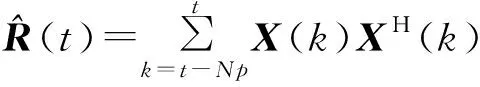
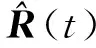
5 结 论

