船载USB瞬时站址残差异常情况分析*
(中国卫星海上测控部,江苏 江阴 214431)
1 引 言
航天测量船参加重大航天发射任务前都要进行多次实战任务的模拟演练。在某测量船模拟演练过程中,准实时数据评估发现测量船实时软件计算的USB瞬时站址数据比对残差曲线异常,所有圈次残差曲线均出现明显倾斜,部分圈次在由小变大的趋势上还出现明显的凸包。同时,各圈次距离系统差也不一致,有的圈次仅有0.3 m,而有的圈次系统差超过了10 m,有的圈次甚至达到了23.3 m,数据出现如此明显的起伏,这种现象难以解释。航天测量船的测控覆盖率在整个航天测控网中占有较高的比例,它提供的测控数据准确与否对测控精度的影响很大。因此,必须在任务实施前分析排查出引起残差曲线异常的原因,确保测量船实时送往中心数据的准确可靠。经过分析,决定采用比对分析方法[1]和试验验证相结合的分析排查方法来分析USB残差曲线异常情况。
2 异常现象分析
将USB数据的比对残差绘图,发现所有圈次残差曲线均出现明显的倾斜,与典型的“剪刀差现象”非常相似,残差或者由小变大(第9、10、25、29、40、41圈),或者由大变小(第14、24、30、45圈),只有第25、29圈的变化趋势稍有差异,在由小变大的趋势上出现了一个明显的凸包。我们知道,“剪刀差现象”是由时间错位引起的[2],如果两组数据比对时间未对齐,由于数据的变化率不一致,将导致比对残差在航捷处符号发生变化,从而导致残差数据出现倾斜。模拟演练的快速评估结果显示,USB瞬时站址残差数据有的圈次变大,有的圈次变小,假如数据存在时间问题,据此可以判定时间错位的现象不是简单的超前或者滞后,而是两者都存在。任务中测量船每秒发出一帧瞬时站址数据,线程启动时刻开始积累数据,20秒区间平滑得到秒节点数据。此环节如果出错,得到的数据将不在秒节点上,而数据评估时与之比对的数据是秒节点上的实测数据,比对结果必然出现“剪刀差现象”。但进一步分析后发现,几艘测量船的比对结果并不一致,有的测量船快速评估结果中残差曲线并未出现异常,不同圈次距离R的系统差一致性很好。在实战软件中该模块的实现模式所有测量船都是一样的,如果是这个原因引起的,应该所有测量船的比对残差都会出现异常,但实际情况并非如此。因此,虽有剪刀差现象但可排除时间错位的可能性。
分析第25、29圈残差的变化趋势,在由小变大的趋势上还出现了一个明显的凸包。在新测量船精度校飞时,由于测站位置参数使用错误,曾出现过类似的残差曲线,难道这次的异常现象也是视差修正错误引起的?为了分析问题,我们先了解一下航天测量船动基座设备姿态系统中有哪些因素在视差修正中发挥着作用。
3 航天测量船动基座设备的船姿系统
海上测量与陆上测控站不同,测量船是在动态条件下进行测量的,有不同于陆上测站的特点。船的位置随时在变化,船体受到摇摆、风浪、海流等内外力的冲击和影响,船体各部分会产生弹性变形,船的姿态也随时在变化。必须在测量设备跟踪被测目标的同时,对船的位置和姿态进行同步测量,测量数据经船位和船姿修正,变成地平系内的数据,才能与整个试验航区建立起联系。可以说,船姿船位修正是航天测量船数据处理所特有的、必不可少的重要环节。
3.1 航天测量船船姿系统
航天测量船船舶姿态测量可分为航向测量和水平基准测量,平台罗经和惯性导航系统的出现圆满地解决了运动载体姿态测量的问题。惯性导航系统是目前航天测量船精度最高的动态姿态测量设备,测量船上众多的精密测量设备都是由惯导提供水平基准和方位基准。在一个载体上,当有两个以上的高精度局部姿态测量需求时,就有变形测量的需要,可以说,船体变形测量是姿态测量的扩展,这是我国海上测控的特有技术。海上测控是利用安装在测量船甲板上的测控设备实施的,而测量船上的这些测控设备跟踪目标的方位基准是船的艏艉线,俯仰基准是甲板平面,站址基准是浮动的惯导三轴中心。由于测量船上有不同的测量设备,为了便于海上测量参数的使用和描述,航天测量船定义了自己专用的坐标系,各种设备的测量数据必须经过坐标变换,统一转到惯导地平系,才能与整个测控网建立起联系,接收并发送数据到测控中心。
3.2 航天测量船专用坐标系之间的关系
惯导地平坐标系、惯导甲板坐标系、测量坐标系就是为航天测量船测控需要专门定义的3个坐标系。惯导地平坐标系和惯导甲板坐标系的坐标原点均在惯导平台的三轴交点,惯导地平坐标系的水平基准面平行当地的水平面,而甲板平面与船体固联,当船浮在水面上时,由于船有摇摆,两平面就不重合了;惯导地平坐标系的X轴指向正北,而惯导甲板坐标系的X轴与船艏艉线平行,所以,这两个坐标系之间相差船摇修正量。
测量坐标系与惯导甲板系的差别有3点:一是坐标原点不一致,测量坐标系原点在测量设备的三轴中心;二是在坞内标校船坐墩条件下,测量设备方位转盘平面与甲板平面相差一个设备的大盘不水平;三是船浮在水面上时,由于测量设备和惯导平台之间有一段距离,因船体变形,所以这两个坐标系之间又多了一个船体变形量[3]。
从上述坐标系的差异描述中可以看出,从测量坐标系向惯导地平坐标系转换时,首先修正测量设备的大盘不水平,然后修正船体变形量,将测量系的坐标原点平移到惯导甲板坐标系的坐标原点后,再修正船摇量。它们之间的关系如图1所示。
4 船姿系统各参数对观测资料的影响试验及数据分析
测量设备在测量船上是沿船艏艉线分散布局的,各设备之间的距离有10 m以上,由于船体并不是一个钢体,各设备基座间存在船体变形。而船摇数据是由惯性导航系统测量的,惯导测量的船体摇摆角,实际上只是惯导基座的摇摆角,不是其它部位的,其它部位与惯导基座之间的差值即为船体变形量。因此,需要在它们之间建立精密的光学联系,以测量出因船体变形引起的三自由度变化角: 艏挠角κb、纵挠角ψb、横扭角θb。变形测量得到的是两个设备基座间的船体变形量(Kbi,ψbi,θbi),而我们要得到的是两个直角坐标间的相对角旋转量(Kb′i,ψb′i,θb′i),即欧拉角。公式(1)~(3)建立了变形实测参数(Kbi,ψbi,θbi)与欧拉角(Kb′i,ψb′i,θb′i)之间的关系[4]:
(1)
φb′i=φbi
(2)
利用3个实测变形角(Kbi,ψbi,θbi)即可唯一地确定变形修正所需的旋转矩阵Bb′。
为便于分析问题,将测量船的坐标变换公式简化描述如下[4]:
(4)
从式(4)可以看出,船舶摇摆(Kc,ψc,θc)、船体变形(Kb,ψb,θb)及设备原点的位置参数(x0,y0,z0)在视差修正中对外测数据均有影响。
4.1 船舶摇摆对观测资料的影响试验及数据分析
测量船船摇数据反映了船体运动的三维姿态,测量船的运动规律除了与船体性能有关,还与其所处的海况和航行工况有关。艏摇角是船艏艉线在水平面上的投影与正北的夹角,测量船对目标实施测量时,是按预先设计的航向作匀速直线航行的,测量船航向会左右摆动,其摆动的幅度与当时的海况有关。纵摇角是指船体纵轴与水平面的夹角,就是船艏抬高或降低的角度,以船艏抬高为正。横摇角是指船体横截面相对水平面的夹角,就是船体横截面向左右倾斜的角度,以右舷下降为正[5]。
为了考察航向修正对观测资料的影响,我们分两种情况进行了试验:一种是用正常的实测船姿数据进行修正,一种是不做航向修正(纵、横摇仍使用实测数据)。处理结束后,比对两组数据,发现航向修正对R、E基本没有影响,对方位角的影响则是1∶1。
以同样的手段对纵摇和横摇数据也进行了试验,较之航向参数,这两个参数的影响就比较复杂。我们知道,当船体产生纵、横摇倾斜时,雷达天线的旋转面也随之倾斜,如同雷达大盘倾斜的情况一样,方位和俯仰角均会产生误差。
从试验结果可以看出,纵摇数据对俯仰角的影响相对较大,E残差变化规律与纵摇角的变化规律基本一致,残差数据的量级与纵摇成一定的比例关系,其系数是方位角的余弦函数。纵摇数据对方位的影响与当前的跟踪性能有关,航捷附近残差变化幅值小于其余时段。纵摇数据对距离R的影响不大,主要体现在随机分量上,其残差在航捷附近的变化幅值也明显小于两端。
横摇对R、E的影响使其残差数据在航捷前后符号发生变化,对俯仰角E的影响还与当前方位A有关,且有正弦效应,其残差曲线在航捷前后出现台阶,幅值和横摇角量级相当,如果此项误差较大,横摇的影响会非常明显。横摇对方位A的影响在航捷附近较明显,导致其残差曲线振荡,变化周期与横摇周期一致。
3个船摇量均不修正,距离R的残差曲线与不修横摇时R的残差曲线变化趋势完全一致,横摇角对距离R的影响比另外两个参数大,但总的影响也只有2 m左右;俯仰数据则同时受纵摇和横摇的影响,且横摇角能改变其残差的变化趋势;影响方位数据的主要是航向。
4.2变形对外测数据的影响试验及数据分析
用比对分析方法对USB数据进行变形修正试验,变形对仰角的影响在-24.9~13.58角秒之间,对方位角的影响在31.0~53.0角秒之间,对距离的影响在-0.07~0.04 m之间。结果表明,变形修正与否对角度的影响较明显,但对斜距基本没有影响。
4.3 测量设备原点坐标位置参数的影响试验及数据分析
从转换公式(4)可以看出,设备原点的坐标位置参数(x0,y0,z0)也是影响处理结果的一个可变因素。为了考察它的影响,将3个坐标参数置零,不进行平移修正,处理后与正常修正结果比对。可以看出,坐标位置参数对角度的影响并不明显,但对距离影响非常大,达到10 m以上。
5 问题排查
从上述试验结果的分析已经知道,变形数据对距离R的影响基本可以忽略不计,因变形数据出现异常导致测距系统差不一致的可能性可以排除。
在船舶摇摆的3个姿态角中,艏摇和纵摇对距离R的影响非常小,横摇的影响较大,尤其对残差曲线变化趋势的影响比较明显,在航捷前后符号会发生变化,势必导致残差曲线出现上升或者下降的现象。横摇数据修正异常,是否就是导致距离残差曲线异常的原因?还需要进一步分析。从表1可以看出,10个圈次的比对结果中,距离R的系统差最大的是第25圈,达到23.3 m,而第25圈横摇数据对R的影响总误差才2.22 m,虽然不能排除它的影响,但可以肯定横摇数据不是导致距离R残差异常的主要因素。
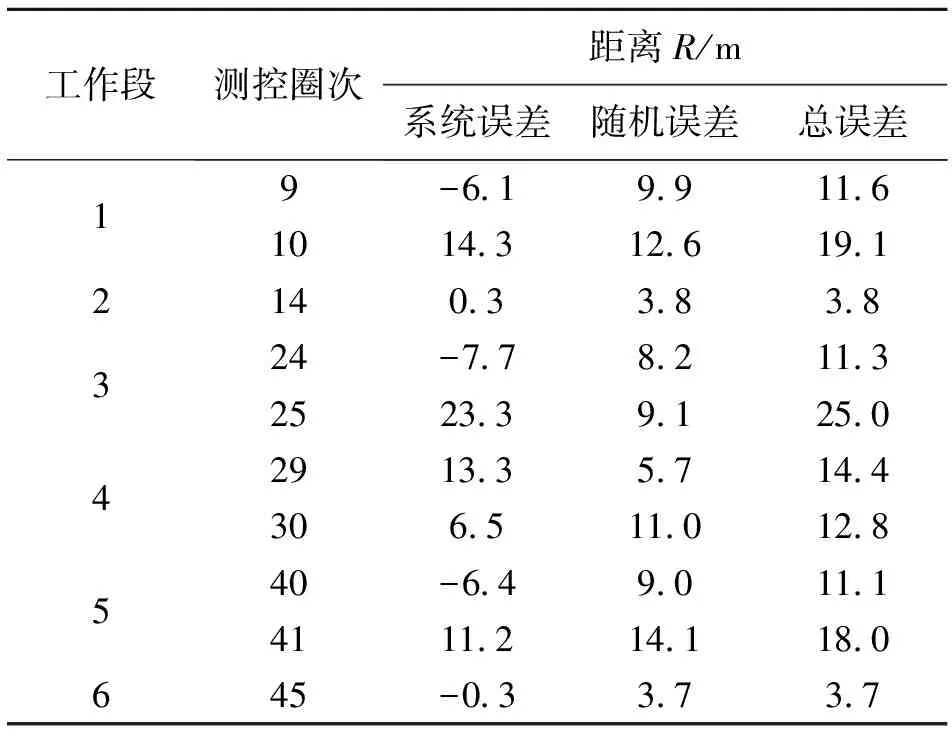
表1 USB瞬时站址比对残差统计结果Table 1 Results of USB instant site compared with residual statistics
设备原点的坐标位置参数对距离R的影响明显,达到10 m,在坐标转换涉及的三类数据中,它的影响最大,而且其残差曲线也出现了凸包,分析后决定把问题的排查思路定位在坐标位置参数的使用上。在USB设备原点的3个坐标位置参数(x0,y0,z0)中,z0基本为零,y0为7 m左右,x0值最大,达到20 m,我们尝试着将设备位置参数X坐标值符号取反后参与坐标转换,发现系统差达24.4 m,证明设备的坐标位置参数对距离R的影响是非常显著的。但作为一个固定不变的常值,它的影响应该是固定的,而实际情况是不同圈次距离R残差的系统差是不一样的。并且,经过仔细核查,该项参数的设置、使用完全正确,完全可以排除坐标参数设置、使用错误的可能性。
不同圈次系统差不一致,这样的错误应该是一些随时在变化的因素造成的。我们从分析各圈次的不同点入手进行排查。在模拟演练时,测量船实施工作段模式和单弧段模式,工作段指测量船有连续多个可跟踪弧段的时段。单弧段模式是指在工作段中测量船对飞行器实施单个跟踪弧段的基本工作模式。在同一个工作段中的每一个单弧段,除测量船工况设计不同外,海况在较短时期内变化不大,参数的使用及设备参试状态的设置基本是一致的。从表1可以看出,即使是在同一工作段中的不同单弧段,距离系统差也相差甚远(如24、25圈,差值达15 m之多)。而同一工作段中不同单弧段工况设计的主要区别是航向,分析比较各弧段的航向与系统误差后,发现距离系统差不一致现象与测量船的航向有关联,当测量船的航向接近正北方向时,距离的系统差就小(如第14圈,航向345°,残差系统差仅0.3 m) (见图2);当远离正北方向时,系统差就偏大(如第25圈,航向213°,残差系统差达到23.3 m)。难道是航向的差异导致系统差的不一致?

图2 USB测距R残差系统差与测量船航向的关系图Fig.2 Relationship between USB range residual system difference and course of a space tracking ship
但从前面的分析我们知道,单一的航向因素对测距的影响非常小,三类参数中只有坐标位置参数的影响比较明显,如果把这两项因素(航向、设备原点的坐标位置参数)的影响叠加在一起,又会带来怎样的变化呢?
分析式(4)可以看出,正常情况下,在修正船体变形量后,将测量系的坐标原点平移到惯导甲板坐标系的坐标原点后,再进行船摇修正。坐标转换是先平移后旋转,也就是说设备原点的坐标位置参数(x0,y0,z0)也参与了船摇修正,即测量船设备原点的坐标位置参数(x0,y0,z0)是要进行航向修正的,如果设备原点的坐标位置参数的航向修正出了问题,结果会怎样呢?如果对坐标位置参数不进行航向修正,又会出现怎样的结果?
6 进一步试验验证
根据上述假设,我们对坐标位置参数(x0,y0,z0)不进行船摇修正,即按式(5)进行坐标转换,发现第25圈距离残差系统差达到22.7 m,距离R的残差曲线在由小变大的趋势上也出现了一个明显的凸包,与模拟演练中出现的残差曲线非常相似。
(5)
根据测量船专用坐标系的定义知道,惯导甲坐标系X轴指向船艏,惯导地平系的X轴指向正北,两个坐标系X轴的指向相差航向修正如图3所示。
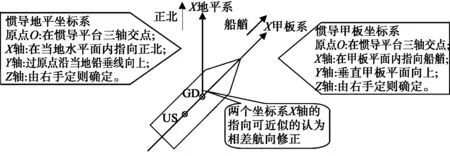
图3 甲板系和地平系之间的关系Fig. 3 Relationship between INS deck coordinate system and INS horizontal coordinate system
如果上述错误存在,当航向接近正北方向时,惯导甲板系X轴的指向也接近正北方向(如图4所示第14圈),与惯导地平系X轴的指向相近,未进行航向修正的坐标位置参数其平移方向与实际方向相近,测距系统差就小;当航向远离正北方向时(如图4所示第25圈),惯导甲板系X轴的指向也远离正北方向,与惯导地平系X轴的指向不一致,未修航向的坐标位置参数平移方向与实际方向相差较大,测距系统差必然变大,所以随着航向的改变,设备原点坐标位置参数对距离R的影响也发生了变化。在模拟演练过程中,由于不同圈次航向不同,也就出现了不同圈次距离R系统差不一致的现象。
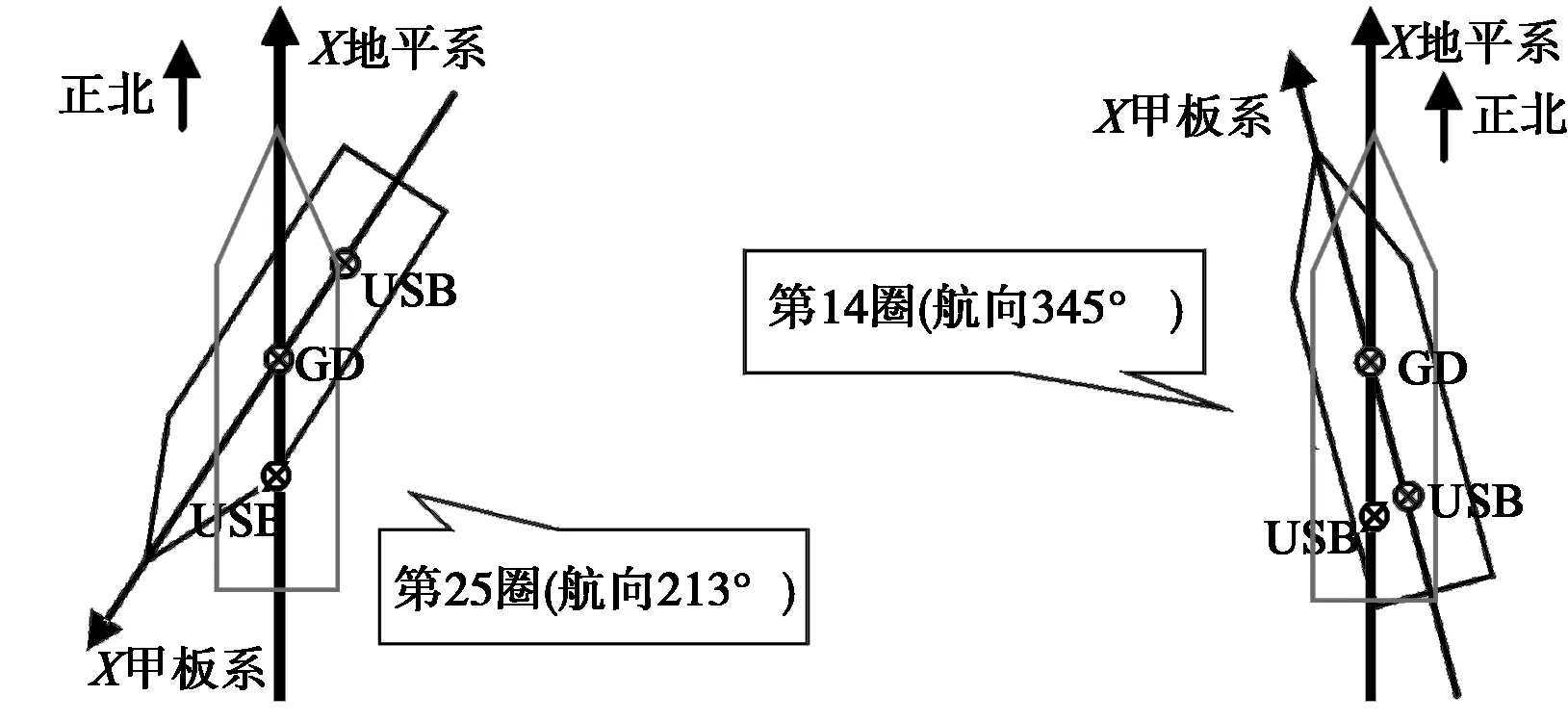
图4 惯导甲板系X轴与惯导地平系X轴的关系Fig. 4 Relationship between axis X of INS deck coordinate system and axis X of INS horizontal coordinate system
为了验证上述分析是否正确,我们将程序按上述假设修改后再与演练过程中实时计算的数据比对,发现两套数据吻合得很好,说明各圈次系统差不一致是由于实时软件使用的视差修正模型对设备原点的坐标位置参数未进行船摇修正造成的。发现问题后,及时改进了视差修正模型,对坐标位置参数增加了船摇修正,同时进行了软件维护,确保了实战软件的正确性。
7 结束语
在影响测量船外测数据的误差源中,除测控设备的测量误差、大气折射修正剩余误差(低仰角跟踪时)、动态滞后误差外,还有船位误差、船摇误差和船体变形等误差,后面两项是海上测量所特有的,这两项误差的修正工作均在视差修正环节完成,其对测量船测量结果精度的影响所占比例能达到20%~30%。测量船采用的是单站定位体制的测控模式,对观测资料的精度要求高,只有保证数据处理方法的准确性,才能确保处理结果的精度满足任务要求。测量船利用改进的视差修正方法修改后的新版软件参与实战任务,准实时数据评估提供的结果显示,所有测控弧段USB瞬时站址数据残差曲线恢复正常,各圈次距离系统差均降至1 m以内。
参考文献:
[1] 李辉芬,张忠华,朱伟康,等.船载设备测量数据处理结果的综合分析方法[J].飞行器测控学报,2008,27(6):65-70.
LI Hui-fen,ZHANG Zhong-hua,ZHU Wei-kang,et al. The Exterior Tracking & Measuring Data Analyzing and Processing of Instrumentation Ship[J].Journal of Spacecraft TT&C Technology,2008,27(6):65-70.(in Chinese)
[2] 李辉芬,朱伟康,周朝猛,等. 基于比对分析技术的船载设备故障分析[J].无线电工程,2009,39(4):30-35.
LI Hui-fen,ZHU Wei-kang,ZHOU Chao-meng,et al. Ship-borne Equipments of Fault Analysis Based on Comparison Analysis Technique[J].Radio Engineering of China,2009,39(4):30-35.(in Chinese)
[3] 江文达. 航天测量船[M].北京:国防工业出版社,2002:13-129.
JIANG Wen-da.Space Tracking Ships[M].Beijing:National Defense Industry Press,2002:13-129.(in Chinese)
[4] 张忠华,等.航天测量船船姿数据处理方法[M]. 北京:国防工业出版社,2009:117-169.
ZHANG Zhong-hua,et al.Space tracking ship attitude data processing methods[M]. Beijing:National Defense Industry Press,2009:117-169.(in Chinese)
[5] 潘良,等.航天测量船船姿船位测量技术[M]. 北京:国防工业出版社,2009:139-158.
PAN Liang,et al. Space tracking ship attitude and position measurement technology[M]. Beijing:National Defense Industry Press,2009:139-158.(in Chinese)

