二次雷达C模式编解码实现*

(四川大学 计算机学院，成都 610064)

1 引 言

空中交通管制(ATC)[1]利用通信、导航技术和监控手段对飞机飞行活动进行监视和控制，保证飞行安全和有秩序飞行。空中交通管制是二次雷达(SSR)应用最普遍的领域。二次雷达[2]是利用发射询问信号并接收目标的应答信号来获得目标信息的雷达，由询问机和应答机两部分组成。首先由地面询问机发射一定模式的询问脉冲信号，当询问信号为A模式时，应答机回答飞机的代码；当询问信号为C模式时,应答机回答飞机的气压高度信息。

目前,在空中交通管制系统中对高度信息的处理，采用的是二次雷达C模式应答编码，而高度编码把其中8个脉冲以格雷(Gray)码编码形式进行组合，由于格雷码属于无权码，不能直接进行运算，所以在对高度信息编解码的过程中需要进行格雷码与二进制码的相互转换。查表法[3]是实现格雷码与二进制码相互转换的常用方法，该方法由于受到建表的影响需要占用大量的存储空间，在处理脉冲个数上受到很大限制，同样也会增加硬件系统的成本，不便于C模式编解码软硬件实现。本文分析了二次雷达C模式编解码的一般实现过程，讨论了高度编解码的一般方法，并归纳、总结了公式法在二次雷达C模式编解码中的应用。

2 格雷码简介

格雷码(Gray Code)是1880年由法国工程师Jean-Maurice-Emlle Baudot 发明的一种编码,因Frank Gray于1953年申请专利“Pulse Code Communication”而得名。

格雷码是一种可靠性编码，它所产生的误码率最低，因为这种编码相邻两个码组之间仅有一位不同，在用于A/D转换时，当模拟量发生微小改变而引起数字发生改变时，格雷码只改变一位，而其它码则有可能改变两位或者多位，所以采用格雷码编码的电路就能以最少的错误在较高的速度下稳定工作。

3 高度编码特征

飞机的飞行高度由国际民用航空组织(ICAO)规定，所要编码的高度范围约为-366～38 618 m(-1 200～126 700 ft)[4]。当机载应答机接收到C模式询问脉冲信号时，应答码为高度编码；高度编码由标准循环码和五周期循环码两部分组成。当数学化的气压高度信息有效时， C模式询问的应答码就由规定的两个框架脉冲和信息脉冲组成，长度为两个字节,应答码高度编码顺序如图1所示。

排序应答码字母1ACVD1D2D4A1A2A4B1B2B4C1C2C411--0标准循环码(Gray Code) 五周期循环码 1

图1 C模式应答码字母的排序
Fig.1 Sorting the letters of mode C response code

标准循环码由D2、D4、A1、A2、A4、B1、B2、B4共8位组成，采用格雷码编码规则,D1位未使用(恒为0),D2代表最高位，该部分编码的增量单位约为152 m(500 ft)；五周期循环码由C1、C2、C4共3位组成， C1代表最高位，增量单位约为30 m(100 ft)，且满足表1的编码规则。

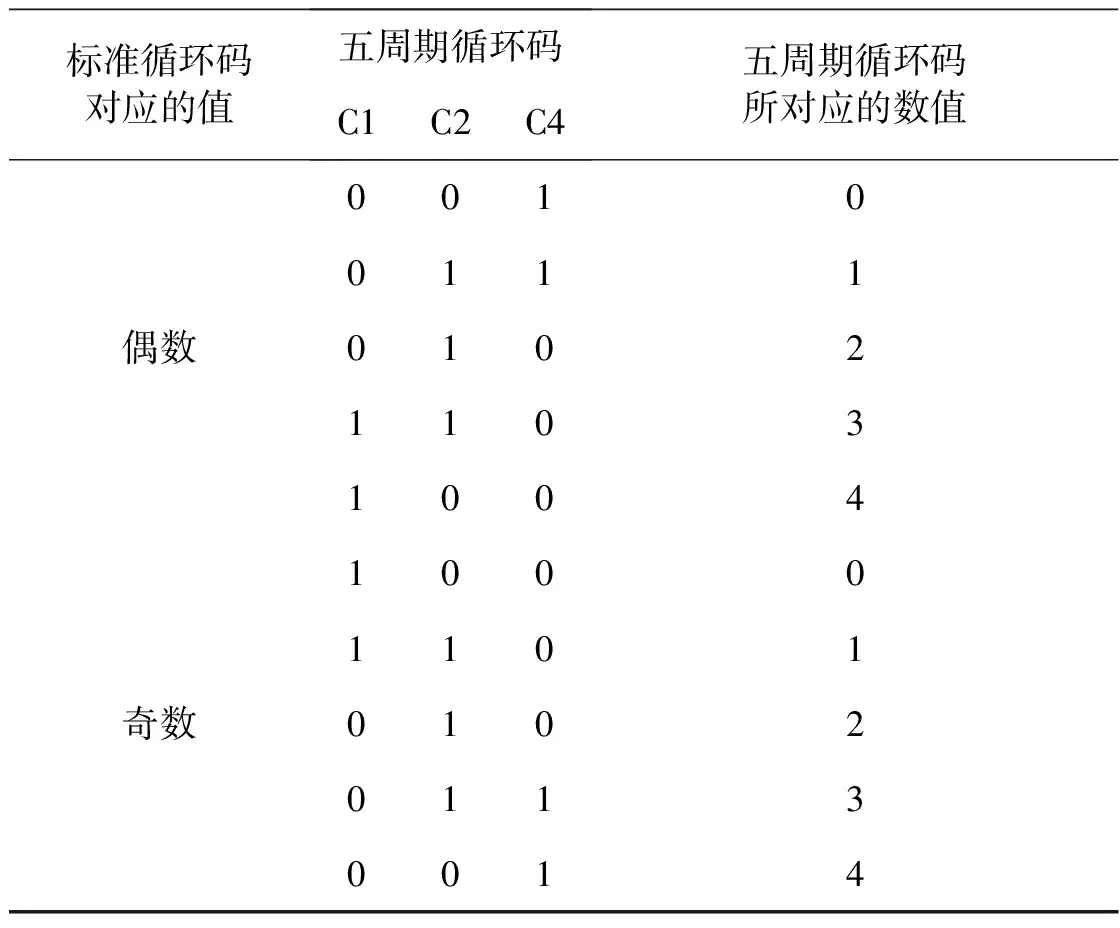
表1 五周期循环码规则

4 高度编解码实现

二次雷达高度编解码实现的一般过程是,当机载应答机接收到C模式询问脉冲信息后，首先将通过气压高度表获得的气压高度值进行编码，以形成应答脉冲信号发回地面，监视雷达接收并处理应答脉冲信号，解码之后的高度信息就可在屏幕上显示出来，从而获取飞机的高度信息。为了保证以较高精度显示飞机的高度值，在高度编解码中使用的是格雷码与五周期循环码组合的编码规则。由图1可知，C1、C2、C4采用五周期循环码编码规则，利用表1的对应规则较易实现数值之间的转换；D2、D4、A1、A2、A4、B1、B2、B4采用格雷码编码规则，实现格雷码与二进制码的相互转换是处理高度编解码的关键。文献[5]中介绍了一种格雷码转换为二进制码的方法,它将一个字节(8位)格雷码划分为高4位和低4位,利用转换规律分别求出高4位和低4位格雷码所对应的二进制码,这种方法在实现格雷码到二进制码的转换，过程略显复杂,并且处理格雷码的位数受到很大限制。以下简要介绍目前常用的查表法在格雷码与二进制码相互转换中的运用，以及公式法在高度编解码中的实现。

4.1 查表法

传统的二次雷达高度编解码中采用的是查表法实现二进制码与格雷码的相互转换，其原理是建一个二进制码与格雷码的对应表，如以4位二进制码建立的表2所示。如果要将一个二进制码转换为格雷码，首先在表中纵向找到要转换的二进制码，然后再在表中横向查找其对应的格雷码，这样就实现了一个二进制码到格雷码的转换。由于二进制码与格雷码之间存在一一对应关系，可以采用类似方法实现格雷码到二进制码的转换。

表2 四位二进制码与格雷码的对应表

这种方法的主要优点有：表中每一个二进制码与它所对应的格雷码都能准确地实现相互转换；方法简单，可用一个数组实现转换操作；执行时间快。

但是，查表法自身的实现原理，决定了它不可避免地存在很大缺陷，主要是因为在实际应用研究中，要转换的脉冲数往往不止4位，有的高达16位甚至32位，这就需要分别建立包含65 536个元素和4 294 967 296个元素的对应表，即便是表1中的8个脉冲，也需要建立包含256个元素的对应表，建立这样大的对应表，费时且容易出错，占用大量的内存资源，软硬件实现较复杂；此外，当处理的二进制码或格雷码位数发生改变时，就需要另外建立新的对应表；软硬件应用的扩展性不强。

文献[3]中阐述了利用查表法实现高度编解码的详细过程。

4.2 公式法

针对查表法在实现二进制码与格雷码相互转换中存在建表繁锁、占用资源多等缺点，同时考虑到二进制码与格雷码之间存在一一对应规则，本文利用格雷码与二进制码之间的相互关系,实现C模式高度的编解码,能够很好地克服查表法建表和查表的复杂操作。

实现二进制码与格雷码相互转换的公式有所不同，以下分别描述这两个公式的基本原理。

(1)二进制码转换为格雷码

二进制码转换为格雷码，其原理是保留二进制码的最高位不变作为格雷码的最高位，而格雷码次高位由二进制码的最高位与次高位异或得到，以此类推，格雷码其余各位与次高位的求法类似。

设BnBn-1Bn-2…B2B1B0为一个二进制码,GnGn-1Gn-2…G2G1G0为其转换所得的格雷码。转换过程是：保留二进制码的最高位不变作为格雷码的最高位，即Gn等于Bn，格雷码的次高位Gn-1则由Bn与Bn-1异或求得，Gn-2则由Bn-1与Bn-2异或求得。以此类推，便可求得相对应的格雷码。用公式(1)来简单描述二进制码转换为格雷码的步骤：

(1)

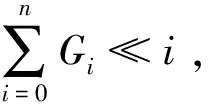
在文献[6]中利用伪代码阐述了高度编码的过程,但没有具体说明二进制码转换为格雷码的实现步骤。在本文中,将式(1)运用到二次雷达C模式高度的编码中,具体的编码流程如图2所示。

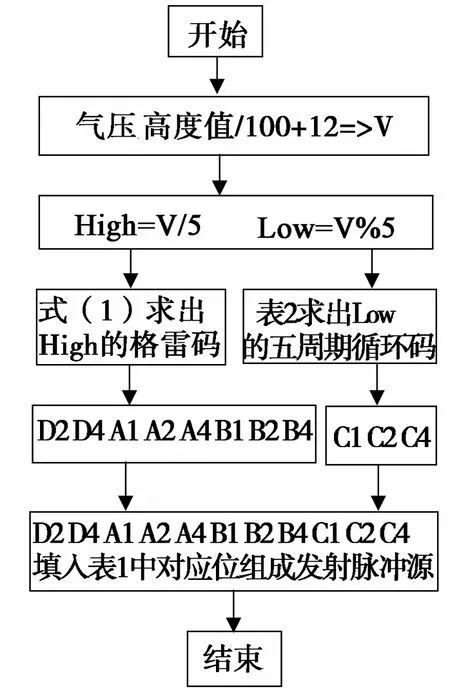
图2 编码流程图Fig.2 Encoding flow chart

说明：要编码的气压高度值不是从0开始的，而是从约366 m(-1 200 ft)开始的，所以将气压高度值除以100后再加上12所得的值才是要编码的值。

(2)格雷码转换为二进制码

格雷码转换为二进制码，其原理是保留格雷码的最高位不变作为二进制码的最高位,二进制码次高位为二进制码最高位与格雷码次高位异或所得,二进制码的其余各位与二进制码次高位的求法类似。

设GnGn-1Gn-2…G2G1G0为一个格雷码,BnBn-1Bn-2…B2B1B0为其转换后的二进制码, 转换过程是：格雷码最高位保持不变,作为二进制码的最高位，即Bn等于Gn，用Bn异或Gn-1得到Bn-1，再用Bn-1异或Gn-2得到Bn-2,依此类推，便可求得相对应的二进制码。用式(2)来简单描述格雷码转换为二进制码的步骤：

(2)

运用式(2)实现高度的解码，具体解码流程如图3所示。

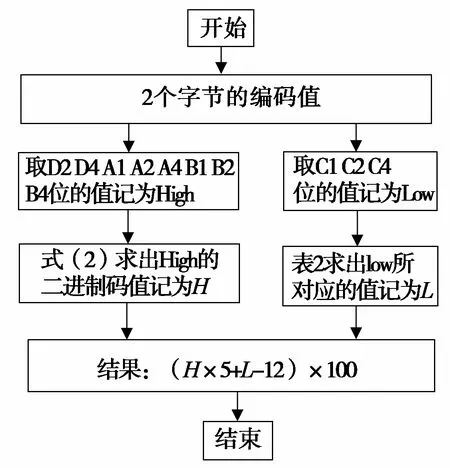
图3 解码流程图

从图1与图2的流程不难发现, 利用公式法实现高度的编解码,省去了建表的步骤,程序实现上不会占用大的存储空间,而且不会受到因处理脉冲位数变化的影响。在实现二次雷达C模式高度编解码的过程中运用公式法处理二进制码与格雷码的相互转换将更加简单、快捷、灵活。

5 实验

表3是从文献[4]附录A中截取的5个高度数据的编码,用以验证4.2中所介绍的方法的有效性和可用性。

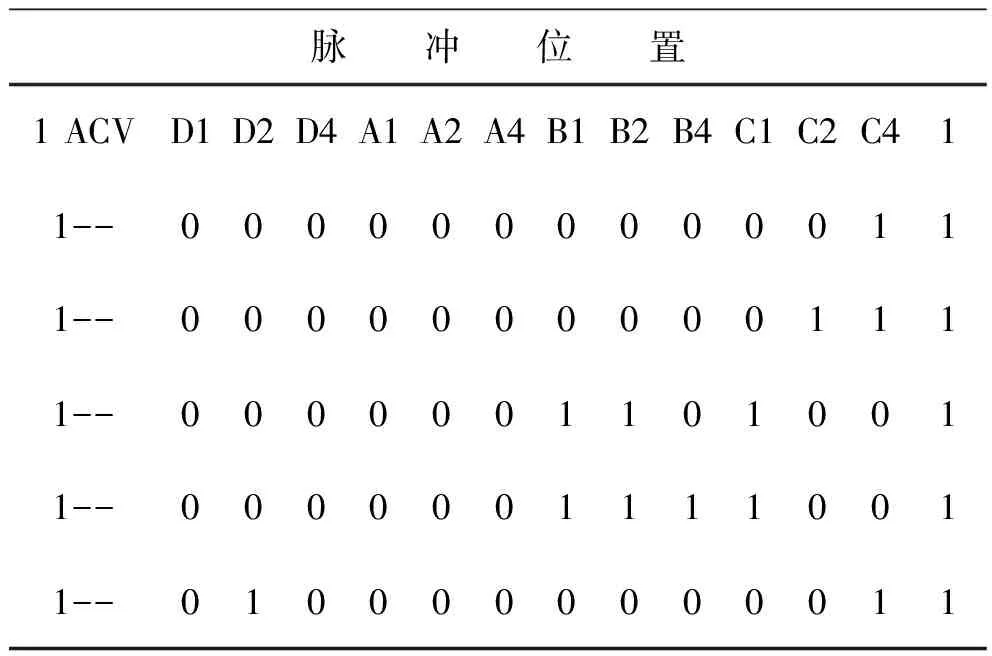
表3 C模式编码

利用图3的解码流程求得表3中的5个编码数据的高度值分别约为-366 m(-1 200 ft)、-335 m(-1 100 ft)、366 m(1 200 ft)、396 m(1 300 ft)、38 618 m(126 700 ft)，这5个高度值与文献[4]附录A的原始值相符。

利用图2的编码流程，对以上求得的5个高度值进行编码，通过编码所获得的5个编码值分别为1、3、52、60、1025，这5个编码值正好等于表3中D2、D4、A1、A2、A4、B1、B2、B4、C1、C2、C4位的编码值。

图4和图5是对高度进行编码和解码分别采用公式法和查表法处理的效率对比图，从图中可以得出结论：公式法在克服了查表法建表繁锁、占用内存资源、操作复杂等缺点的基础上，同样达到了理想的执行效率。

图4 编码效率对比

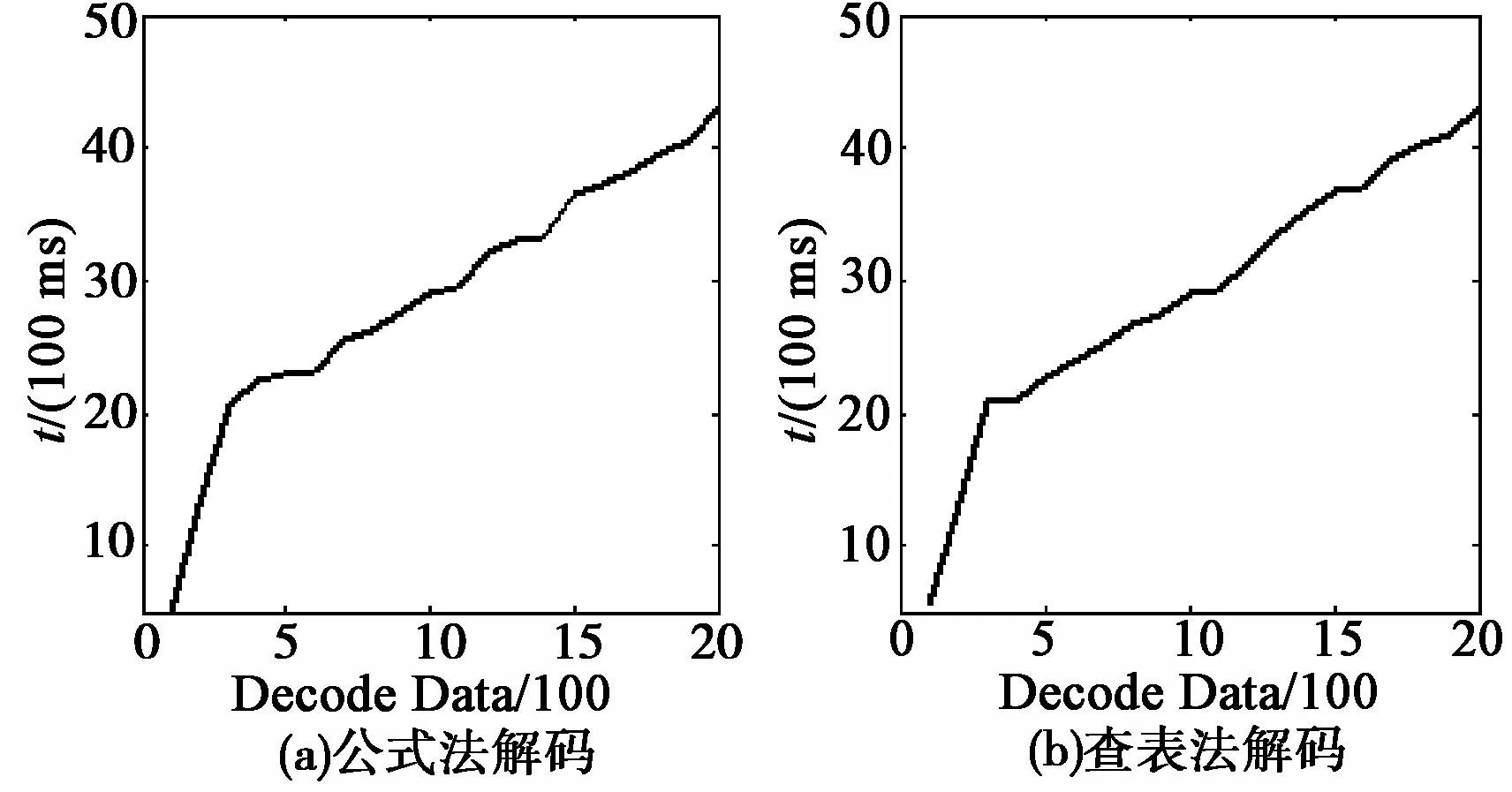
图5 解码效率对比

通过上述实验，验证了公式法在实现格雷码与二进制码相互转换中的准确性和可行性，同时也说明，运用公式法实现二次雷达C模式高度编解码能够达到可靠的准确性和时效性要求。

6 结束语

本文针对二次雷达高度编解码的实现过程进行阐述，并实现了在高度编解码中的公式法处理方法。该方法不同于以往的查表法，随着空中交通密度的增加，所需处理的目标数目也随之增加，运用公式法处理二次雷达高度码，在克服了查表法存在建表繁锁、占用内存资源多等缺点的情况下，不仅提供了方便快捷的实现方式，同样也保证了在空中交通管制系统中的实时性和准确性监控。

在东芝雷达真实环境下引接的数据进行分析和实验，结果很好地验证了该方法的有效性和适用性。此外，运用该方法处理其它类型雷达数据的可用性还有待于进一步研究。

参考文献：

[1] 黎廷璋.空中交通管制机载应答机[M].北京：国防工业出版社，1992.

LI Ting-zhang. Air Traffic Control Airborne Transponders[M].Beijing:National defense industry Press,1992.(in Chinese)

[2] Stevens M C. Secondary Surveillance Radar [M]. Norwood, MA: Artech House,1988.

[3] 陈健.机载二次雷达应答机的研制[D].成都:电子科技大学,2008.

CHENG Jian. The Development of Airborne SSR Transponders[D].Chengdu:University of Electronic Science and Technology of China,2008.(in Chinese)

[4] MH/T 4010-2006,空中交通管制二次监视雷达设备技术规范[S].

MH/T 4010-2006,The Technical Specifications of Air Traffic Control Secondary Surveillance Radar Equipment[S]. (in Chinese)

[5] 马彦霞,陈玉国,司爱国.PLC中将格雷码转换成二进制码一种运算方法[J].微计算机信息,2006,22(28)：101-102.

MA Yan-xia,CHEN Yu-guo,SI Ai-guo. An Operational Method Involving the Conversion of the Gray Code to Binary Code in PLC[J].Micro Computer Information,2006,22(28)：101-102.(in Chinese)

[6] 高伟,陆海静,郑海波.某型空管应答机高度源模拟器电路设计[J].现代电子技术,2008(21)：57-59.

GAO Wei,LU Hai-jing,ZHENG Hai-bo. Circuit Design of Simulated Altitude Source for Certain Air-control Transponder[J].Modern Electronics Technique,2008(21)：57-59.(in Chinese)