碳纤维增强聚合物基复合材料修补空心柱体结构的屈曲分析

王 蔓，白 瑞 祥，杨 继 新

( 1.大连工业大学 机械工程与自动化学院， 辽宁 大连 116034;2.大连理工大学 工业装备结构分析国家重点实验室， 辽宁 大连 116024 )

0 引 言

碳纤维增强聚合物基复合材料(CFRP)在工程方面的应用一直是研究的热点问题。纤维增强复合材料具有重量轻、强度高、耐久性好、施工简单等诸多优点，因此在结构加固修补技术中得到了愈来愈广泛的应用[1-4]。国内外对粘贴CFRP修补结构进行力学试验的研究取得较大进展[5-8]，粘贴CFRP后结构的力学性能大幅提高。采用纤维增强树脂基复合材料对含损伤杆件进行加固修复可以抑制裂纹的扩展，延长结构寿命。采用有效的方法对修复工艺参数进行优化设计，预测修补效果对节约修复成本，提高修复成功率具有重要作用。鉴于此，作者建立了CFRP加固含损伤金属结构的有限元模型，对受轴向压缩载荷含损伤钢结构进行了模拟修补，并与基于能量原理推导的CFRP加固柱体屈曲载荷的理论公式做了比较，得到了钢结构的轴向压缩载荷临界屈曲结果；通过参数讨论，得到了一些对工程有益的结论。

1 CFRP加固空心柱体结构屈曲分析的解析方法

对于图1所示轴心受压空心柱体，在中间用 CFRP进行加固。服役期内出现裂纹或壁厚减薄造成损伤。设损伤区位于柱体中部，用CFRP沿柱体轴向进行加固，在压缩载荷P作用下发生弯曲变形。

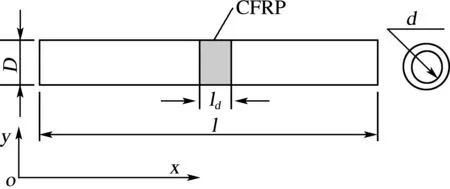
图1 CFRP加固受压空心柱体示意图

Fig.1 Sketch of hollow cylinder strengthened with CFRP under compression loading

理想压杆在两端铰支下，其临界力[9]为

Pcr=π2EIl-2

(1)

式中，Pcr为压杆处于临界状态的临界压力，EI为抗弯刚度，l为压杆长度。

假定加固空心柱体弯曲时仍符合平截面假定，则组合截面的抗弯刚度为

(2)

式中，d为柱体内径，Dd为损伤空心柱体外径，h为CFRP层厚度，(EI)g为CFRP加固后组合截面抗弯刚度，Ef与Es分别为CFRP沿空心柱体轴线方向和空心柱体的弹性模量。

当空心柱体弯曲时，忽略剪切变形能，则加固后弯曲变形能为

(3)

式中，ld为空心柱体中部损伤区长度，M为构件的截面弯矩，I为完善空心柱体惯性矩。

对于图1坐标系，设中部位移为δ，则可假定空心柱体挠曲线方程为

(4)

可用式(5)计算端部轴向位移

(5)

而外力功ΔW=Pδ2π2/4l，且ΔU=ΔW，则加固后构件屈曲载荷可写成：

2 CFRP加固空心柱体结构有限元分析

2.1 屈曲分析的有限元控制方程

采用有限元法对加固前后的屈曲载荷进行分析，根据稳定性理论和最小势能原理可以得到在小变形情况下结构的屈曲平衡方程

加固前

(7)

加固后

(8)

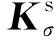
(K+λKσ)u=0

(9)

式(9)是一个典型的特征值问题，即

det |K+λKσ|=0

(10)

在ANSYS中有多种求解方法，这里仅提取其一阶特征值λ1，则结构屈曲临界载荷Pcr=λ1P，P为所施加的初始压缩载荷。

2.2 有限元模型

对于图1所示CFRP加固空心柱体结构，CFRP、柱体与胶层均视为线弹性，并认为其黏结界面为理想黏结。对于CFRP和空心柱体均可以采用壳单元模拟，分别以CFRP中性面和空心柱体的中性面建立两个分离的柱面，且二者都可采用层合壳单元剖分，空心柱体在输入单元参数时视为各向同性单层板。CFRP和空心柱体相对应的部分在网格剖分时保证节点与单元的一一对应，如图2所示，可通过约束方程将两部分连接起来。 对于分别位于CFRP和空心柱体上的2个节点，若二者位于同一法线上，则这两个节点可以视为一个节点对，在单元坐标系内，CFRP节点位移(u1，v1，w1，θx1，θy1，θz1)与相应的空心柱体上的节点位移(u2，v2，w2，θx2，θy2，θz2)满足以下协调关系：

图2 CFRP与柱体连接有限元实现

(11)

式中，H为空心柱体的壁厚。

3 算例分析

轴心受压空心柱体，其长度l=4 m，内外径分别为：d=140 mm，D=150 mm，设柱体为钢制，则其与T300/QY8911制成的CFRP(沿轴线粘贴CFRP)弹性模量分别为：Es=200 GPa，Ef=135 GPa，CFRP单层厚度为0.125 mm，边界条件为两端铰支。

对于裂纹损伤，CFRP起到止裂的作用，柱体壁厚不受损伤影响。图3给出了CFRP长度为1 m，分别采用有限元法和解析法求解加固柱体在轴向压缩载荷作用下的屈曲载荷与CFRP厚度的关系曲线。当采用CFRP加固后，其临界屈曲载荷随着CFRP层的厚度逐步增大，有限元法和解析法的曲线变化趋势比较符合，结果在定量分析上的差别则决定于两种方法的自身原因，有限元法的精度与模型误差、网格离散误差以及数值积分精度等因素有关，而解析法精度主要取决于补片刚度对结构整体变形的影响是否满足公式(4)假定的挠曲线方程，图3给出的结算结果表明对本算例条件，两种方法均有效。图4给出了CFRP为2 mm时临界屈曲载荷与CFRP加固长度的关系曲线。从图4曲线可以看出，当柱体壁厚不受损伤影响时，随着CFRP加固长度的增加，屈曲载荷明显增大。

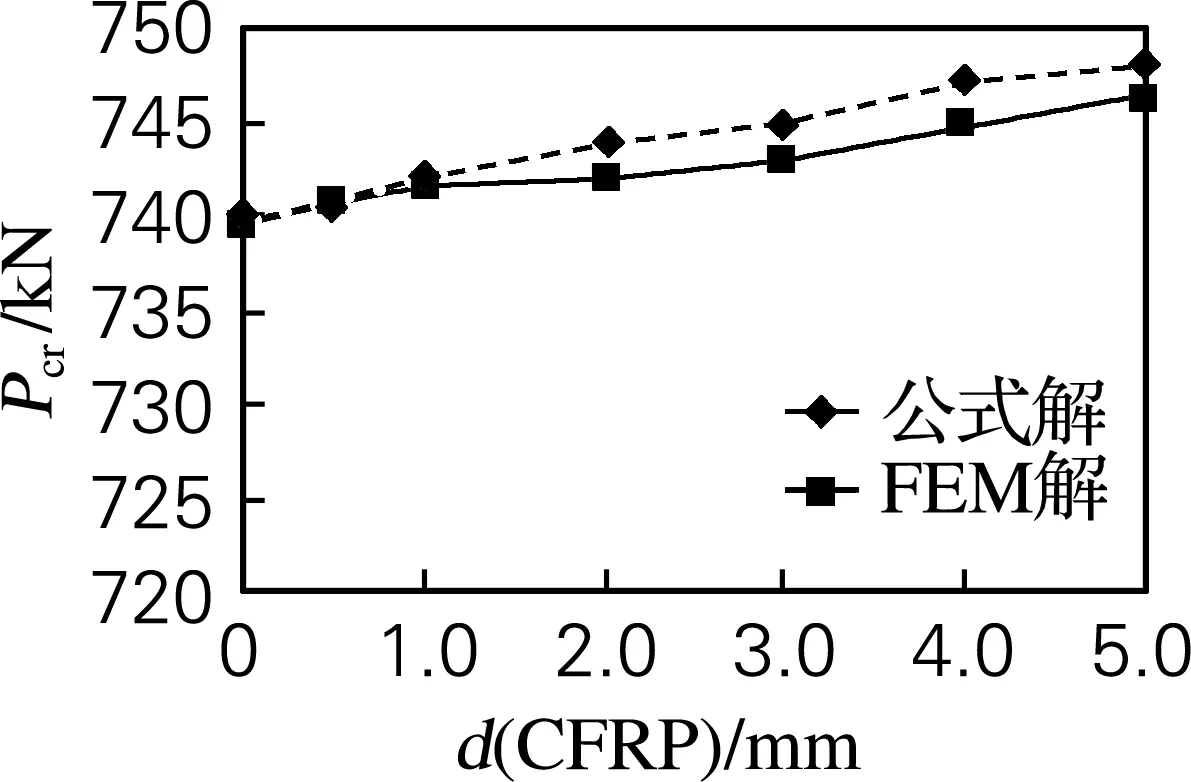
图3 屈曲载荷与CFRP厚度曲线关系

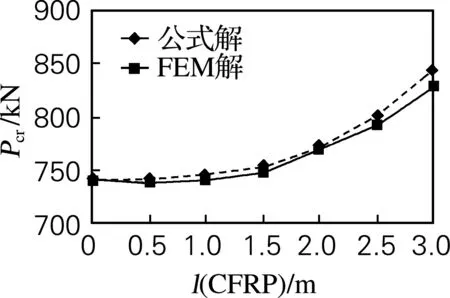
图4 屈曲载荷与CFRP加固长度关系

考虑腐蚀损伤，则柱体损伤部分壁厚则予以折减，损伤部分尺寸：Dd=146 mm，ld=1 m时，其他条件同上。采用CFRP轴向加固含损伤柱体的屈曲载荷与CFRP厚度关系曲线如图5所示，图6给出了有限元法的含裂纹损伤柱体与含腐蚀损伤柱体的屈曲载荷与CFRP厚度关系曲线。从图5、6中可以看出，采用CFRP加固提高了其屈曲载荷，随着CFRP厚度逐渐增大，含损伤柱体的屈曲载荷随之提高，对于本算例修复方案，改善幅度不大，且CFRP加固的含腐蚀损伤空心柱体仍比CFRP加固裂纹损伤空心柱体的屈曲载荷值低，这说明CFRP补片增加的弯曲刚度不能弥补结构自身因腐蚀损伤所削弱的弯曲刚度。

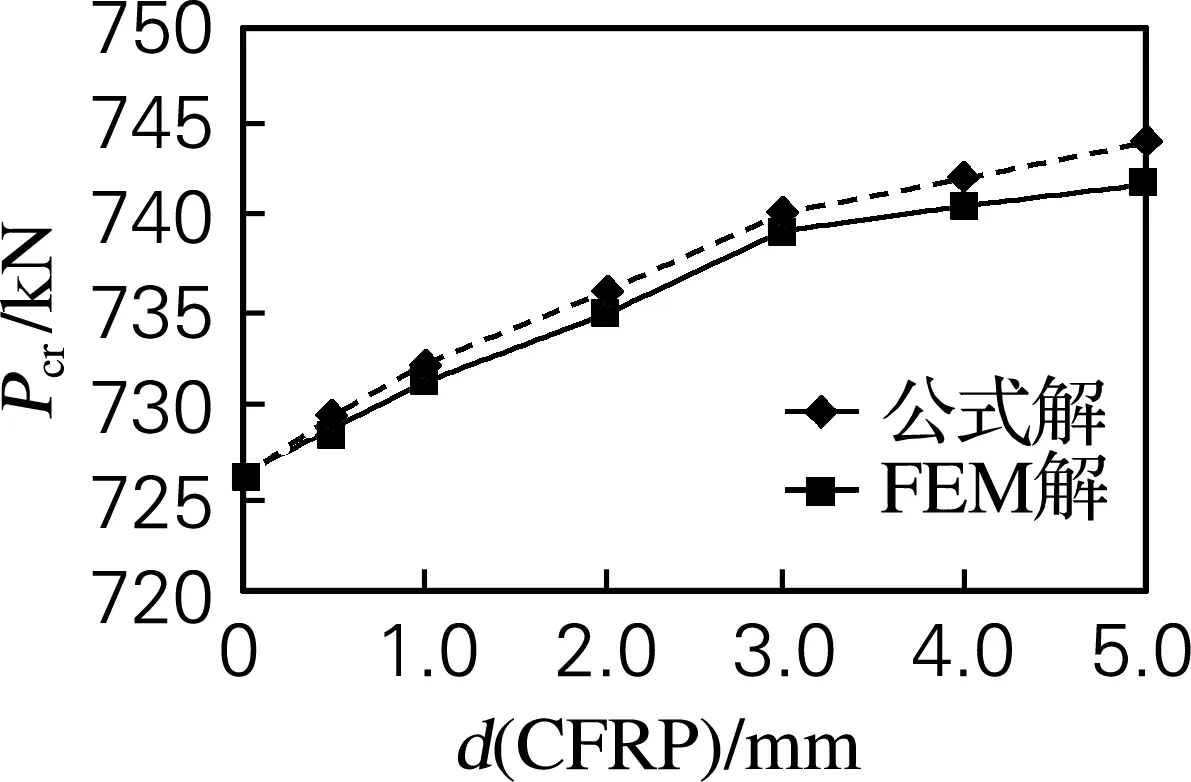
图5 含损伤CFRP柱体屈曲载荷与CFRP厚度关系

Fig.5 Buckling load vs. thickness of CFRP with damage

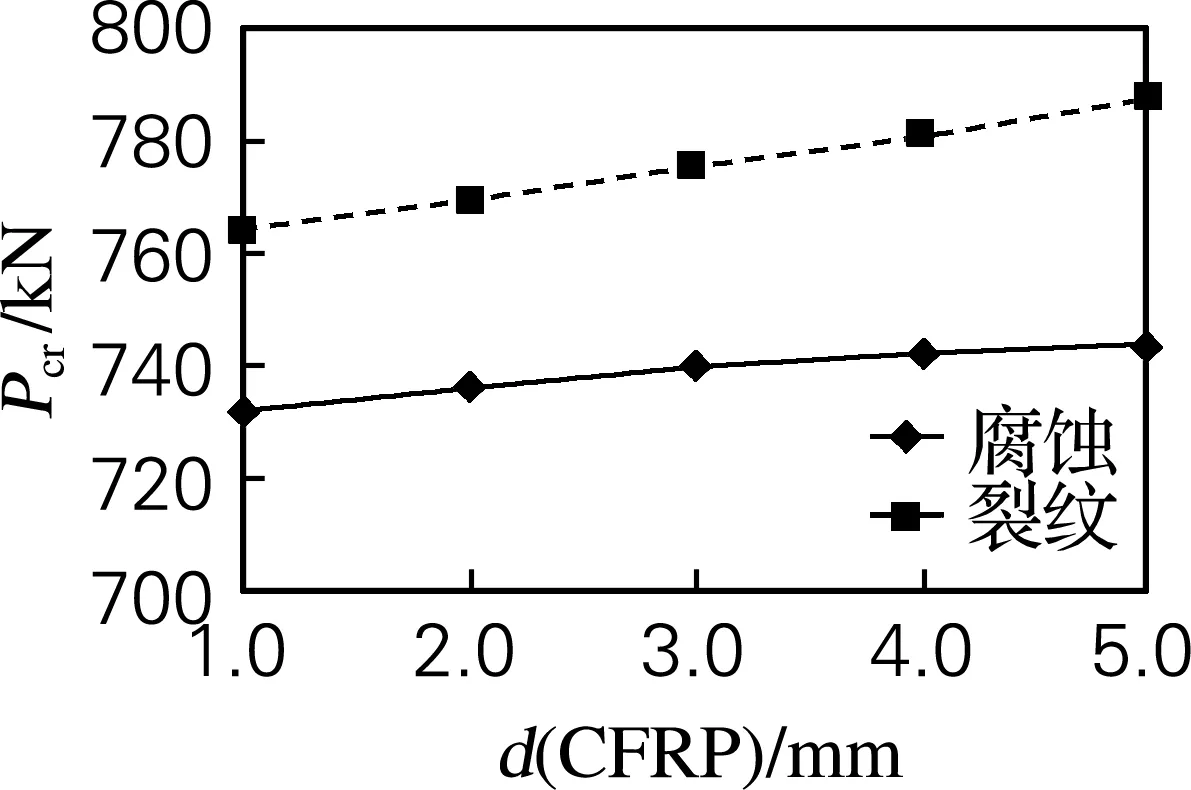
图6 含损伤柱体屈曲载荷与CFRP厚度关系

Fig.6 Buckling load vs. thickness of CFRP with crack and corrosion

CFRP补片厚度为2 mm时，含腐蚀损伤柱体的临界屈曲载荷与CFRP加固长度的关系曲线如图7所示。从图7可以看出，考虑柱体壁厚腐蚀损伤时，在腐蚀区域长度较小的情况下，随着CFRP加固长度的增加，屈曲载荷增大。对比图4不考虑腐蚀损伤的临界屈曲载荷曲线，当腐蚀损伤长度较长时，增加CFRP加固长度不再提高柱体的屈曲载荷，这是因腐蚀损伤长度和CFRP补片长度同步增加，柱体的壁厚发生减薄导致抗弯刚度下降，采用CFRP所增加的刚度仍低于腐蚀损伤造成的刚度下降，屈曲载荷随着损伤长度的增加而减小，这是由于模型中损伤部分长度和补片长度是一致的，CFRP补片增加的弯曲刚度已低于结构因腐蚀而损失的弯曲刚度。因此在实际修补时，应布置足够的纤维方向平行于轴线的补片，以提高CFRP补片的弯曲刚度或等效弹性模量。

图7 腐蚀损伤的屈曲载荷与CFRP加固长度关系

Fig.7 Buckling load vs. length of CFRP with corrosion

4 结 论

对粘贴CFRP加固受压空心柱体结构进行了屈曲分析，有限元数值仿真结果与理论公式结果符合很好，证明了有限元模型的有效性；对于轴向受压受腐蚀损伤的构件进行修复时在考虑强度条件的同时，还应考虑修复对刚度补偿的效果；对于单纯裂纹损伤空心柱体，采用轴向粘贴CFRP对提高受压结构屈曲载荷效果显著，提高CFRP参数可提高结构整体刚度，如增加CFRP缠绕层数、粘贴长度可提高结构刚度，进而提高了结构的屈曲载荷；而对于轴压下腐蚀损伤造成壁厚折减的空心柱体其抗屈曲性能下降不容忽视，在进行修复方案设计时应合理安排各铺层的纤维铺设方向，保证补片具有足够的弯曲刚度，否则只是单纯增加补片的厚度和长度效果并不明显。

[1] 普瑞斯特雷 M J N, 赛勃勃 F. 桥梁抗震设计与加固[M]. 北京:人民交通出版社, 1997:1-15.

[2] KHALIFA A, NANNI A. Improving shear capacity of existing RC T-section beams using CFRP composites[J]. Cement & Concrete Composites, 2000, 22(1):165-174.

[3] LI J C, BAKOSSA S L, SAMALIA B, et al. Reinforcement of concrete beam or column connections with hybrid FRP sheet[J]. Composite Structures, 1999, 47(3):805-812.

[4] LIGNOLA G, PROTA A, MANFREDI G, et al. Non-linear modeling of RC rectangular hollow piers confined with CFRP[J]. Composite Structures, 2009, 88(1):56-64.

[5] ALAWI H, SALEH I E. Fatigue crack growth retardation by bonding patches[J]. Engineering Facture Mechanics, 1992, 42(5):861-868.

[6] SEN R, LIBY L, MULLINS G. Strengthening steel bridge sections using CFRP laminates[J]. Composites Part B:Engineering, 2001(2):309-322.

[7] 彭福明,郝际平,岳清瑞,等. 碳纤维增强复合材料加固修复损伤钢结构[J]. 工业建筑, 2003, 33(9):7-11.

[8] 张宁. 碳纤维增强复合材料加固修复损伤钢结构静力与疲劳应用试验研究[D]. 北京:冶金工业部建筑研究总院, 2003.

[9] 王守新. 工程力学[M]. 北京:化学工业出版社, 1998:240-241.