一个 Gelfand-Kirillov维数 1的 Hopf代数的例子

史美华

(浙江外国语学院理工学院,浙江杭州 310012)

一个 Gelfand-Kirillov维数 1的 Hopf代数的例子

史美华

(浙江外国语学院理工学院,浙江杭州 310012)

构建了一个 Gelfand-Kirillov维数 1的 Hopf代数的例子.从而证明,除了无限循环群的群代数 kΖ、无限二面体群的群代数 kD和无限维 Taft代数外,还存在其他的诺特、仿射、正则、素的 Gelfand-Kirillov维数 1的 Hopf代数.

Hopf代数;Gelfand-Kirillov维数;公开问题;无限 Taft代数

1 引 言

本文中,k是一个代数闭域且所有的代数都是指 k-代数.我们先给出一些定义,一个代数成为仿射的如果他作为代数是有限生成的;一个代数称为正则的如果它的整体维数是有限的;一个代数A称为素的如果对任意 x,y∈A,如果 xAy=0则 x=0或 y=0.更多的信息见文献[1].在文献[2]中,作者提出了以下的公开问题:除了无限循环群的群代数 kΖ、无限二面体群的群代数 kD和无限为 Taft代数外是否还有其他的诺特、仿射、正则、素的 Gelfand-Kirillov维数1的 Hopf代数?

设 n是一个偶数,定义一个结合代数 A(n,q)如下:它由 x,g,s和 g-1生成,满足的关系为gg-1=g-1g=1,xg=qgx,xn=1-gn,sx=-xs,s2=1,sg=gs.这里 q∈k是一个 n-次本原单位根.余乘法、余单位和对极分别以以下列方式定义:

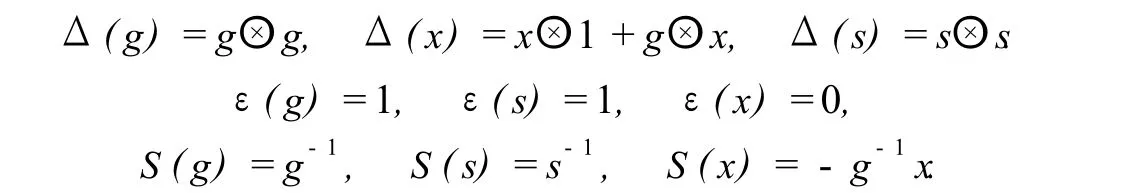
本文的主要结果就是证明上面定义的代数是一个诺特、仿射、正则、素的 Gelfand-Kirillov维数 1的 Hopf代数,从而我们对上述问题给出了肯定的回答.

我们将不加解释地利用一些 Hopf代数常用记号和基本事实,详见文献[3].

2 例 子

为了比较,我们回顾一下无限维 Taft代数的定义.设 n,m和 t均为正整数,q为一个 n-次本原单位根.令 H是一个结合代数,由 x和 g生成,且满足以下关系

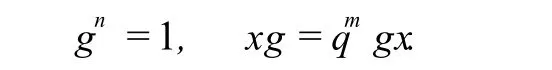
余乘法Δ,余单位ε,和对极 S分别定义为:

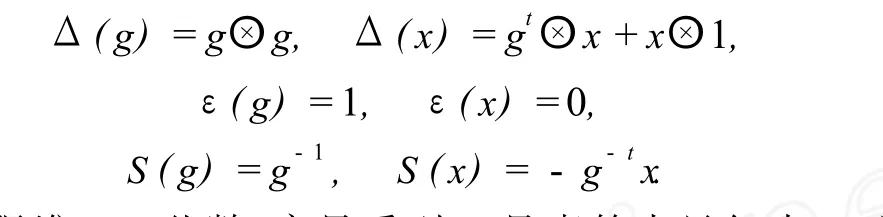
这个 Hopf代数 H称为无限维 Taft代数.容易看到 H是素的当且仅当 qm还是一个 n-次本原单位根.它是诺特、仿射 PIHopf代数,其整体维数为 1.

命题 2.1 A(n,q)是一个 Hopf代数

证明 我们将证明分为以下几步:

步骤 1 Δ是一个代数同态.为此,只需证:

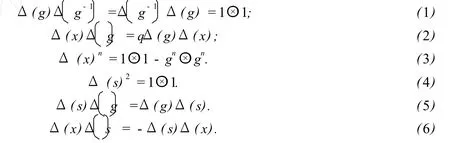
我们只证式(3),因为其他证明相对很容易.对于式(3),

步骤 2 Δ是余集合的.由步骤 1,只需考虑生成元就行了.即只需证明

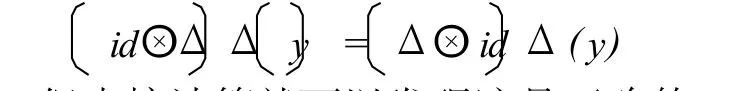
对 y=g,y=g-1,y=s和 y=x.但直接计算就可以发现这是正确的.

步骤 3 S是一个代数反同态,ε是一个代数同态.为证 S是一个代数反同态,只要验证以下的等式:

只证式(9),其余的证明很简单.事实上,

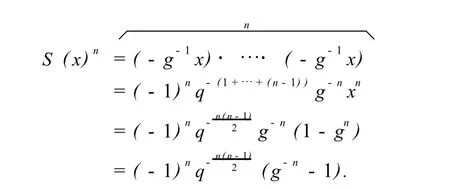
从而为证式(9),需证

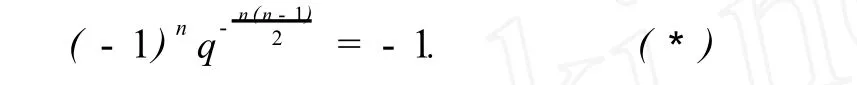
由于 n是偶数,

ε是一个代数同态的证明是容易的,此处不再赘述.

步骤 4 我们有 (ε⊗id)Δ(z)=z=(id⊗ε)Δ(z),z′S(z″)=ε(z)=S(z′)z″对 z∈A.

事实上,由步骤 3,只需对 z=g,z=g-1,z=s和 z=x证明即可.但通过直接计算即可得.

由步骤 1～4,可知A(n,q)是一个 Hopf代数.对于这个 Hopf代数,下面的引理是显然的.

引理 2.2 A(n,q)是诺特、仿射的.

对于一个代数B,我们用 GK(B)来表示B的 Gelfand-Kirillov维数.

引理 2.3 A(n,q)是 PI代数且 GK(A(n,q))=1.

证明 显然,A(n,q)作为 k〈g〉≅kZ-模是一个有限模.由于 kZ是交换的,Gelfand-Kirillov维数为 1,所以由文献[1]的命题 8.2.9(ii)知A(n,q)是 PI代数且 GK(A(n,q))=GK(kZ) =1.

对于一个代数B以及子集 I⊂B.我们用 (I)来表示 I生成的理想.B的整体维数记为 gl. dimB.对于B-模N,其投射维数记为 p.dimBN.

引理 2.4 gl.di mA(n,q)=1.

证明 我们用M来表示平凡A(n,q)-模 k.由于文献[4],只需证 p.di mA(n,q)M=1.

显然 x不是零化子,因为 xM=0,所以M不是自由A(n,q)-模的子模,这意味 p.dimA(n,q)M≠0.

设 I=(x),因为 x不是零化子,所以作为 A(n,q)-模,A(n,q)x≅A(n,q)这意味 p. dimA(n,q)(A(n,q)/I)=1,从而对任意自由 A(n,q)/I-模 F,我们有 p.dimA(n,q)F=1注意到 A/I≅k(Zn×Z2).这是半单的 (由于我们已经假定存在 n-次本原单位根且 n是偶数),所以(A(n,q)/I)M是自由 A(n,q)/I-模的直和项.从而 p.dimA(n,q)M=1.

引理 2.5 A(n,q)是素的.

证明 由素的定义,直接计算可以得到.

定理 2.6 A(n,q)一个诺特、仿射、正规、素的 Gelfand-Kirillov维数 1的 Hopf代数且与kZ,kD和无限维 Taft代数不同构.

证明 由命题 2.1和引理 2.2-2.5知,A(n,q)是一个诺特、仿射、正规、素的 Gelfand-Kirillov维数 1的 Hopf代数.

直接考虑这些 Hopf的代数的类群元素,就可以发现他们是互不同构的.

[1]McConnell J C,Robson J C.Noncommutative Noetherian Rings[M].New York:JohnW iley and Sons,1987.

[2]Lu D M,Wu Q S,Zhang J.Homological integral of Hopf algebras[J].TransAMS,2007,259(10):4945-4975.

[3]Montgomery S.HopfAlgebras and TheirActions on Rings[M].Chicago:DepaulUniversity,1993:82.

[4]LorenzM E,LorenzM.On crossed prouducts of hopf algebrs[J].Proc AMS,1995,123(1):33-38.

An Example of Hopf Algebras of Gelfand-Kirillov D i mension 1

SH IMeihua
(School of Science and Technology,Zhejiang International StudiesUniversity,Hangzhou 310012,China)

This paper defines a new algebraA(n,q),and proves thatA(n,q)is a Noetherian, affine,regular and prime Hopf algebra of Gelfand-Kirillov dimension 1 and hence gives an ans wer to an open question:Infinite cyclic group algebrakΖ、infinite dihedral group and infinite dimensional Taft algebras are examples of affine prime regular Hopf algebras of GK-dimension 1.

Hopf algebra;Gelfand-Kirillov dimension;open question;infinite Taft algebra

O153.3

A

1671-6574(2010)05-0092-04

2010-08-14

课题项目:浙江省 2009年度教师教育科研项目

史美华(1963-),女,浙江嘉兴人,浙江外国语学院理工学院教授.