《数学机械化》中组集合完备化定理的改进研究
于 健,蒋 鲲
(1.大庆师范学院 科研处,黑龙江 大庆 163712;2.黑龙江大学 教务处,黑龙江 哈尔滨 150080)
随着计算机的发展和普及,数学机械化的重要性愈加显著,数学机械化为数学研究提供了一个有力工具,数学机械化的方法已经用于自动证明定理、计算机图形学、智能CAD和机器人等的研制中。由科学出版社出版、吴文俊先生所著的《数学机械化》对数学机械化方法进行了系统而全面的阐述,具有很高的学术价值。定理4.1.27[1]是《数学机械化》这本书的第四章计算机代数的若干问题中关于整数组完备化部分的一个重要定理,它从理论上证明了一个完备组集合CT就是包含在CT中的某一自约化集合T的完备化,且给出了一个在有限步内从CT得到T的算法。但通过进一步的学习,我们发现当CT中第i个位置具有最大坐标的组是比它序次低的某个组的倍数时,存在着一系列的反例,反例中完备组集合CT和得到的自约化集合T的完备化是不相等的。
1 原定理的描述
定理4.1.27:对于任意一个完备的组集合CT,存在唯一的自约化的组集合TCT,使得CT=Comp(T)。此外,有一个算法在有限步内从CT得到T。
证明:让我们把CT中的组按照降序t1>t2>tN排列,从第一步i=1开始到i=N,让我们去掉ti,如果它是CT中某一个比ti低的组的倍数,那么最后剩下的组集合T显然是一个所要求的自约化的集合。这样的自约化的组集合的唯一性可在下面的论述中看到。
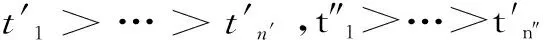
2 反例
反例:考虑一个完备的组集合CT={t1,t2,t3,t4},t1=(2,3),t2=(1,3),t3=(2,2),t4=(1,2)。
解:首先我们把CT中的组按降序排列t1>t2>t3>t4,然后再利用定理4.1.27中的算法在有限步内从CT得到T。
第二步:观察t2,因为t2□t4,且t2>t4,我们去掉t2;
第三步:观察t3,因为t3□t4,且t3>t4,我们去掉t3。
因此我们得到自约化集合T={t4}={(1,2)}及max(T)=(1,2),那么T的完备化Comp(T)={t4},显然CTComp(T)。
通过分析算法,我们发现之所以出现这种结果是因为在组集合CT中存在着这样的一些组集合CTi,它们是在第i个位置具有最大坐标的一些组构成的组集合,CTi中的任意一个组t在CT CTi中能找到某一个组,使得t是这个找到的组的倍数,由定理4.1.27中的算法,在有限步内t是要被去掉的,那么所有组的某个位置的最大坐标也就被去掉了,这样我们得到自约化的组集合T的极大组和CT的极大组就不一致了,因此我们得不到CT=Comp(T)。例如反例中CT1={t1,t3},CT2={t1,t2},在CT1中存在t1□t2,且t1>t2,我们去掉t1及t3□t4,且t3>t4,我们去掉t3; 在CT2中存在t1□t3,且t1>t3,我们去掉t1,及t2□t4,且t2>t4,我们去掉t2。最后我们得到的自约化组集合T的极大组max(T)=(1,2) ,而原来的完备的组集合CT的极大组max(CT)=(2,3) ,因为max(T)≠max(CT),所以CT≠Comp(T)。
3 改进的定理4.1.27
鉴于上面提到的反例,只要在CTi中存在组t,而它不是CTCTi中某个组的倍数,我们就可以找到唯一的自约化的组集合T,使得CT=Comp(T)。因此把这个条件加入原定理,提出改进的定理4.1.27。
改进的定理4.1.27 对于任意一个完备的组集合CT,如果对于∀i=1,…,n,∃t∈CTi⊂CT,使得t不是组集合CT CTi中某个组的倍数,其中CTi={t|Coori(t)=maxi(CT)},则存在唯一的自约化的组集合T⊂CT,使得CT=Comp(T)。此外,有一个算法在有限步内从CT得到T。

4 一个实例
例如:考虑一个组集合CT={t1,t2,t3,t4},其中t1=(2,3),t2=(1,3),t3=(2,2),t4=(2,1)。
杂文引经据典,用事实说话,有形象,有故事。阅读杂文,往往可以学到古今中外、天上地下的各类知识,尤其读到那些闻所未闻的名人轶事,会觉得眼前一亮,如同发现新大陆,不能不“喜洋洋者矣”。此为二乐。
解:首先把CT中的组按降序排列t1>t2>t3>t4,max(CT)=(2,3) 则Comp(CT)= {t1,t2,t3,t4},有CT=Comp(CT) ,因此CT是一个完备的组集合。
接下来我们找出CT中的组集合CT1和CT2,验证组集合CT是否满足改进的定理4.1.27的条件。
CT1={t1,t3,t4},存在t3∈CT1,t3不是组集合CT CT1中组t2的倍数;
CT2={t1,t2},存在t2∈CT2,t2不是组集合CTCT2中组t4的倍数。
因此组集合CT满足改进的定理4.1.27的条件,根据改进定理证明中提到的算法在有限步内从CT来得到T。
第一步:观察t1,因为t1□t3,且t1>t3,我们去掉t1;
第二步:观察t3,因为t3□t4,且t3>t4,我们去掉t3;
最后得到T={t2,t4},而max(T)=(2,3) 则Comp(T)= {t1,t2,t3,t4},所以CT=Comp(T) 。
5 结论
通过研究对定理4.1.27的充分性条件进行了补充,提出了改进的定理,改进的定理使得完备组集合CT和得到的自约化集合T的完备化是相等的,而且给出的算法能在有限步内从CT得到T。
[参考文献]
[1] 吴文俊.数学机械化[M]北京:科学出版社,2003:75-76.
[2] 吴文俊. 数学机械化研究回顾与展望[J].系统科学与数学,2008,28(8):899-904.
[3] 高小山.数学机械化进展综述[J].数学进展,2001,30(5):386-404.

