二叉排序树在动态检索中的应用研究

顾卫杰，钱月霞

（常州机电职业技术学院，江苏 常州213164）

二叉排序树在动态检索中的应用研究

顾卫杰，钱月霞

（常州机电职业技术学院，江苏 常州213164）

在信息系统广泛应用的今天，数据查询的效率越来越受人们关注，以往的顺序查找法查询效率低，很难满足大数据量的查询，本文提出一种基于二叉排序树的动态检索方法，并结合实例，阐述了二叉排序树的构造、平衡、查询等操作，大大提高了检索效率。

二叉排序树；动态检索；平衡

随着计算机技术的发展，电子商务成为新的商业媒介，各类信息系统应运而生，数据检索成为信息系统中最频繁典型的操作，如何提高查询效率成了各类信息系统急待解决的问题。目前大多数信息系统对数据库表的查询操作采用的是顺序查找法，即用所给关键字与数据库表中记录按顺序逐个比较，直到查找到满足条件的记录，时间复杂度为O（n）[1]，这种方法最容易实现，但当数据量很大时，查询效率很低。二分法查找是另一种查找方法，它要求线性表中的结点按关键字值升序或降序排列，查找时不必逐个顺序比较，直接与中间位置的关键字比较，若相同，则查找成功，若给定值大于该关键字的值，则在后半部分进行折半查找，否则在前半部进行折半查找，二分查找效率较高，时间复杂度为O（log n），但对数据的存储格式有要求，必须是顺序存储。本文提出了一种基于二叉排序树的动态检索方法，并以超市管理系统为例，给出二叉排序树的应用过程。该方法查找效率类似于二分法，对于数据需要频繁增加、删除时，可以很方便的实现。

1 二叉排序树的构造

1.1 二叉排序树的特点

二叉排序树（Binary Search Tree），是具有下列性质的二叉树：①若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；②若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；③它的左、右子树也分别为二叉排序树。

作用于二叉排序树上的基本操作的时间与树的高度成正比，对一棵含n个节点的完全二叉树，这些操作的最坏情况运行时间为O（log n），但如果树是含n个节点的线性链，则这些操作的最坏情况运行时间为O（n）。

1.2 二叉排序树的构造方法

根据数据表中的信息，我们可以建立二叉排序树，表中的每行记录看成一个包含若干数据项的数据结点，为这个结点设置ID （结点编号）、NAME（结点名称）、FATHERINFO（结点的父结点信息）、SONINFO（结点与父结点关系信息）等属性，用FATHERINFO字段表示出该结点的父结点信息，用SONINFO字段表示出该结点是左子树还是右子树，当FATHERINFO字段为NULL时，表示该节点为根结点，SONINFO字段用0和1分别表示该结点的左子树和右子树。如表1建立的COMMODITY_TREE表结构。

表1 COMMODITY_TREE表结构

1.3 构造实例

根据超市管理系统中商品信息表里的数据，我们选用毛巾、香皂、卡通书、电饭锅、篮球、按摩器六件商品为例来说明构造过程。把以上六种商品的信息补充到COMMODITY_TREE中，可得到表2，其中FATHERINFO和SONINFO中的值可根据二叉排序树的性质获取，构造的二叉排序树如图1。

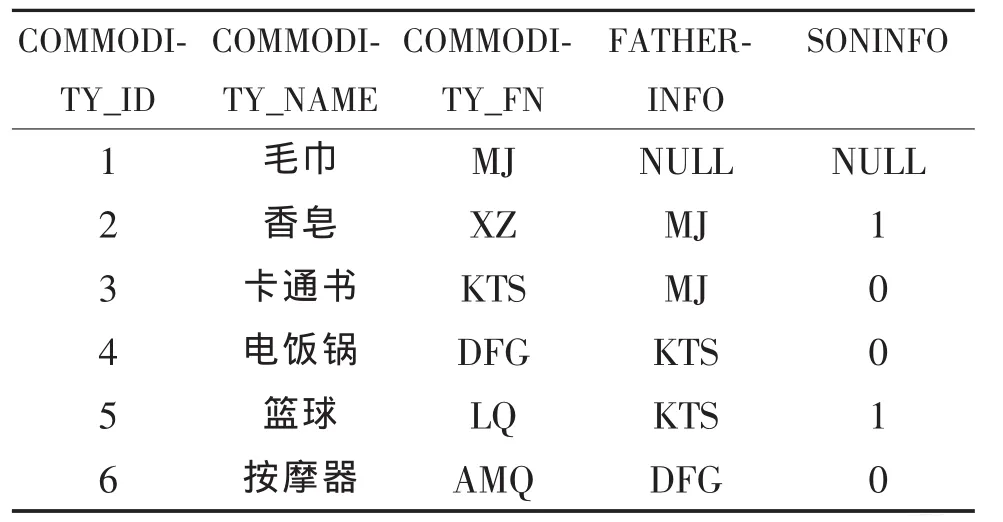
表2 COMMODITY_TREE关系表

2 二叉排序树的平衡

2.1 二叉排序树平衡算法

二叉排序树方便查找、插入、删除等操作，其复杂度为O（log n），但这是个“期望值”，如果二叉排序树失去平衡，相应的查找时间将增加，在最坏情况下，如果插入的关键字有序时，构造的二叉排序树变成单支树，平均查找时间变成 （n+1）/2。因此必须对二叉排序树进行平衡操作，使之成为“平衡二叉排序树”，在“平衡二叉排序树”中任何节点的两个子树的高度最大差别为1，节点的平衡因子是它的右子树的高度减去它的左子树的高度。平衡因子为 1、0或 -1的节点被认为是平衡的，否则该节点被认为是不平衡的，并需要重新平衡这个树[2]。

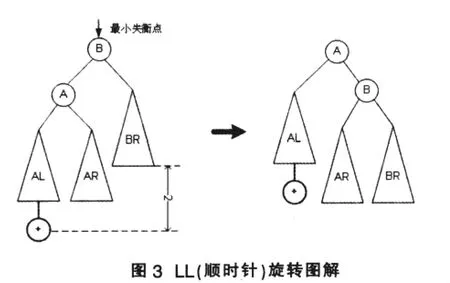
平衡调整的算法是旋转法，分别针对不同失衡结构采用 LL（顺时针）旋转、RR（逆时针）旋转、LR（先顺后逆）、RL（先逆后顺）4种转法，使其达到平衡状态。本文给出LL（顺时针）旋转的图解表示，如图3所示。

2.2 平衡二叉排序树

由图1可看出，该二叉树左子树高度为3，右子树高度为1，根据该二叉树的左右深度之差，求得其平衡因子系数为-2，所以该二叉树不平衡，需要对其进行LL（顺时针）旋转，根据旋转算法，旋转后树形结构如图2所示，再调整二叉树商品关系表，如表3所示。

表3 调整后的COMMODITY_TREE关系表

3 商品信息的动态操作

3.1 节点的插入和删除

插入和删除节点会引起二叉排序树表示的动态集合的变化，要反映出这种变化就要修改数据结构，但在修改的同时还要保持二叉排序树的性质，插入一个新元素而修改树结构相对来说比较简单，但在删除操作时情况要复杂一点。

3.1.1 插入

为将一个新值 v插入二叉排序树 T，可调用过程TREE-INSERT。传给该过程的参数是个节点z，且有key [z]=v，left[z]=NIL，right[z]=NIL。该过程修改T和z的某些域，并把z插入树中的合适位置[3]。算法思想：从根节点开始，沿树下降，指针x跟踪这条路径，而y始终指向x的父节点。根据key[z]与key[x]的值比较结果，决定向左子树或向右子树搜索，直到x成为NIL。这个NIL位置即插入z的地方。算法如下：

3.1.2 删除

从二叉查找树中删除一个节点，可分为三种情况：

（1）节点是一个树叶，没有子女。这种情况，直接删除即可；

（2）节点有一个子女。这种情况，将父节点对该节点的引用改为对其子女的引用即可；

（3）节点有两个子女。如果删除了该节点，其下的两个子女就成了两棵孤立的树了。有两种方法可以解决这一问题：归并删除法和复制删除法[4]。

归并算法的思想：将节点的两个子树合并成一棵树，然后将它连接到节点的父节点上。根据二叉排序树的性质，右子树中的每个键都大于左子树的键，因此最好的方法是寻找左子树中键最大的节点 （即最右边的一个节点），并将其作为右子树的父节点。对称地，也可以找到右子树中键最小的节点（即最左边的一个节点），并将其作为左子树的父节点。

复制算法的思想：节点有两个子女时可以把该节点左子树中的最大节点（或者右子树中的最小节点）的键复制到该节点中，并删除左子树的最大节点（或右子树的最小节点）。这个算法不会增加树高，但是如果删除和插入同时多次进行，也存在一个问题：算法是不对称的，如果每次都删除左子树的最大节点，将会使整棵树向右倾斜。为了解决这个问题，可以对算法的对称性作一个简单的改进。算法交替地从左子树和右子树中复制删除。

3.2 检索

将用户输入的要查询的商品名称转换为各拼音的首字母，与COMMODITY_TREE表中COMMODITY_FN（商品名称首字母）字段信息依次比较各字母串中的字符，直到找到与用户输入商品名称拼音首字母相同的商品名，若首字母相同，还需进一步比较COMMODITY_NAME是否相同，因为有可能出现不同商品名其首字母相同的情况。

查询算法如下：

由以上算法得知，查询的时间复杂度为O（log n），优于顺序查找。当对商品信息进行维护时，也可以利用动态检索的方式，根据二叉排序树的添加、删除的算法对结点进行操作，然后再判断是否平衡，并将之调整为平衡二叉排序树。

4 功能的扩展

为了便于超市管理者了解客户的查询情况，可以在设计COMMODITY_TREE表结构时增加一个计数属性，把客户对商品的查询次数记录下来，并设定一个阈值，及时提醒商家添加新商品，同时根据商品的浏览次数，也可作为进货的依据，提供决策信息。

5 结 语

随着关系数据库技术的应用越来越广泛，利用数据库技术、结构化查询语言来研究基于关系数据库表格的外存储结构的数据结构有着实际的意义，二叉排序树操作灵活，支持动态查询，应用到数据量较大的系统中可以大大提高查询效率。

[1]魏勇.基于关系数据库表树的数据结构研究[J].深圳信息职业技术学院学报，2006(3).

[2]张渊，余小清，万旺根.空间二叉树排序查找算法及其在网络游戏中的应用[J].计算机应用，2007(6).

[3]吴洲.散列表构造与查找的动态实现 [J].电脑知识与技术，2004(12).

[4]黄水松，於朝晖，李世平.一种最佳二叉排序树的动态检索算法[J].武汉大学学报，2000(6).

责任编辑 王荣辉

The Application Research on Dynamic Search Based on Binary Search Tree

GU Weijie，QIAN Yuexia
（Changzhou Institute of Mechatronic Technology,Changzhou Jiangsu 213164，China）

With the widely used of information systems,the efficiency of the data query becomes more and more important.It is difficult to meet the large amount of data query because of the low efficiency of sequential search.This paper presents a dynamic search method based on Binary Search Tree.And it also explains the structure of the tree as well as the method of balance and querying.It really improves the query efficiency.

Binary Search Tree;dynamic search;balance

TP39

A

1674-5787（2010）03-0149-03

2010-03-31

顾卫杰（1980—），男，江苏常州人，硕士，常州机电职业技术学院，讲师，主要研究方向为数据库技术、软件工程。