带锯齿冠叶片振动特性的数值模拟

王小宁, 陈 勇, 杜朝辉, 欧阳华

(上海交通大学机械与动力工程学院,上海200240)

汽轮机叶片是汽轮机的关键零件,承担着把蒸 汽热能转化为机械能的重要任务,对汽轮机的安全运行至关重要[1].在工程实际应用中,带锯齿冠叶片得到了大量使用.叶片在气流周期性扰动力作用下可能会发生异常振动,导致高周或低周疲劳失效.利用叶冠之间的干摩擦产生阻尼,是一种有效抑制叶片振动、降低叶片动应力的方法,因此,有必要对带锯齿冠叶片的振动特性进行研究.

本文以某汽轮机带锯齿冠动叶片为研究对象,计算了其固有频率和模态,并基于“滞后”弹簧摩擦模型,分析了其干摩擦阻尼减振特性.

1 “滞后”弹簧摩擦模型

在研究摩擦阻尼器时,用来描述作用于接触面上的干摩擦力的数学模型主要有两种[2-3]：库仑摩擦模型与“滞后”弹簧摩擦模型.但是,采用库仑摩擦模型不能准确表达出相对位移较小时的力学关系;而在“滞后”弹簧摩擦模型(图1)中,接触面之间的滑移不是突然发生的,当滑动载荷小于临界摩擦力时,接触点存在一定的弹性变形,叶片仍可以存在一定的振幅,只有当叶片振幅过大,滑动载荷大于临界摩擦力时,摩擦接触点之间才产生相对滑移.假设位移x作正弦变化时,“滞后”弹簧摩擦模型的力与位移的关系示于图2.从图2可看出：该“滞后”弹簧摩擦模型的轨迹为闭合的平行四边形.由于这种模型更接近实际,因此,在对叶片进行的研究中,摩擦阻尼几乎全部采用了“滞后”弹簧摩擦模型.

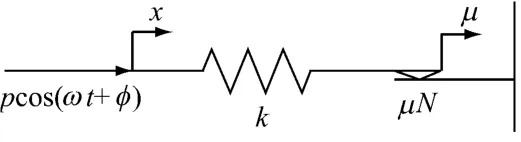
图1 “滞后”弹簧摩擦模型Fig.1 Hysteretic spring friction model

在图1中,p为激励力幅值;φ为初始相位角.

图2 “滞后”弹簧摩擦模型的力与位移的关系Fig.2 Relationship betw een force and disp lacement of hysteretic spring friction model

采用谐波平衡法,可求得只保留一个谐波(即在谐波平衡方程中只保留基波项)时干摩擦阻尼器的等效刚度K eq和等效黏性阻尼系数C eq的表达式[4]：

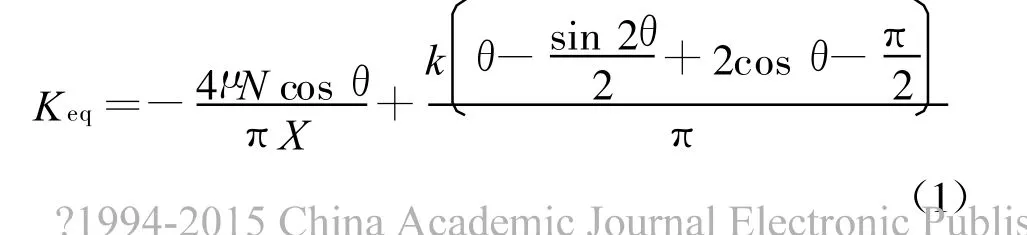
式中：k为相邻接触面间的弹性剪切刚度,N/m;μ为摩擦因数;N为正压力,N;X为相邻接触面间的相对位移幅值,m;ω为激励力角速度,r/s.

图3为相邻叶冠接触面处局部施加的M atrix 27单元.将得到的等效刚度和等效阻尼的值分配到M atrix 27单元上,并以此来模拟冠间的刚度和阻尼.然后,对叶冠相邻接触面的接触部分进行网格细化,施加多对M atrix 27单元,如图3中虚线所示.

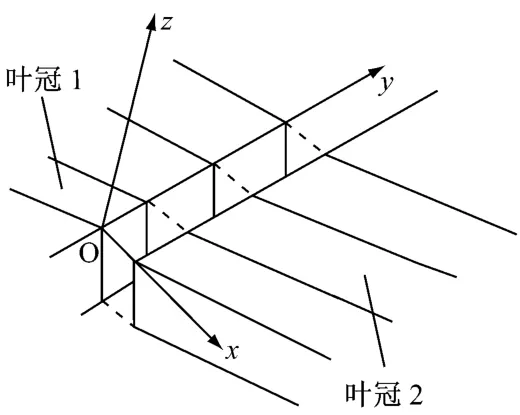
图3 相邻叶冠接触面处局部施加的Matrix 27单元Fig.3 Elem en t of MATRIX 27 im posed on part of contact surface between ad jacent blade sh rouds

2 算 例

2.1 带锯齿冠叶片的有限元模型

图4和图5分别为某汽轮机带锯齿冠叶片的无叶根叶片的几何模型与有限元模型.叶片采用Solid 45号8节点单元进行划分,单元总数为1 176个,节点总数为1 485个,叶身型面底部通常采用固支约束条件.

图4 无叶根叶片的几何模型Fig.4 Geometricmodel of“Z” b lade w ithou t root

图5 无叶根叶片的有限元模型Fig.5 Finite elementm odel of“Z” blade w ithout root

该带锯齿冠叶片的工作温度为57.2°C,进、出汽边压力(静压)分别为24.0 kPa和15.7 kPa,材料为0Cr17Ni4Cu4Nb(沉淀硬化型不锈钢).表1给出了不同温度下叶片材料的密度和弹性模量.表2给出了不同温度下叶片材料的热膨胀系数.

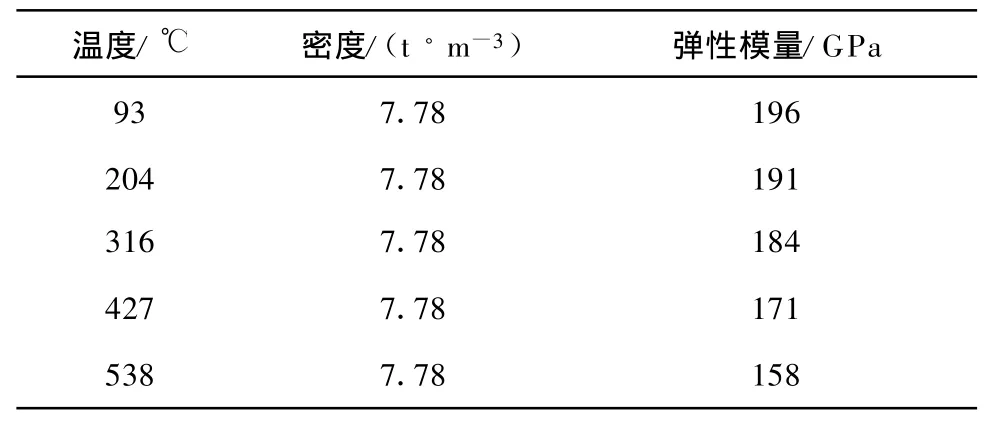
表1 不同温度下叶片材料的密度和弹性模量Tab.1 Density and elastic modu lus of b lade＇smaterial under different temperatures

表2 不同温度下叶片材料的热膨胀系数Tab.2 Thermal expansion coef ficient of blade＇smaterial under different temperatures

2.2 单个叶片和整圈叶片的模态与频率

表3为不同转速下单个叶片的前4阶固有频率,其中100%转速代表3 000 r/min,由此可以推出不同转速百分比所表示的速度值.

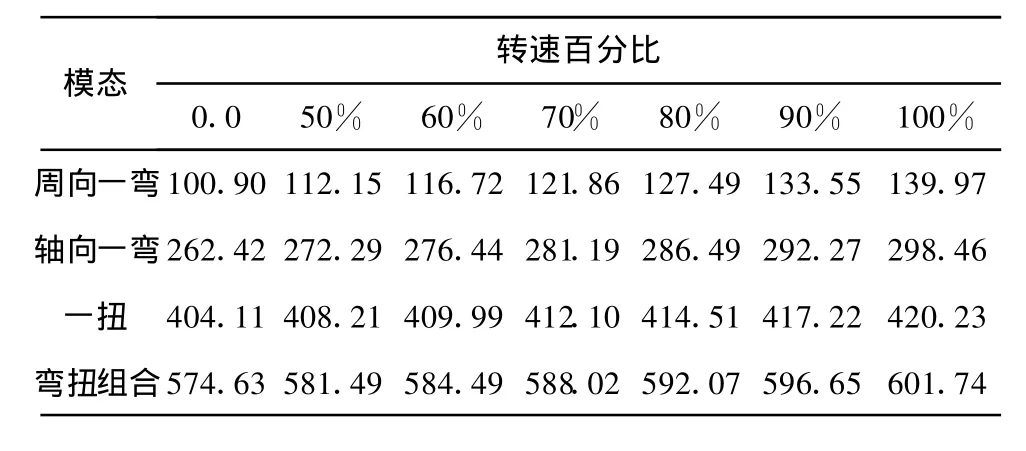
表3 不同转速下单个叶片的前4阶固有频率Tab.3 Front four natural frequencies of single blade under different rotation speeds H z

从表3可知：随着转速的提高,该叶片在各阶模态下的振动频率的数值也增大,在周向一弯、轴向一弯、一扭和弯扭组合下的增大幅度依次为38.7%、13.7%、3.98%和4.72%.可见,转速的变化对周向一弯下的固有振动频率影响最大.根据相关数据,该级整圈共有78个叶片.在Ansys软件中建立有限元模型时,采用的是在周向上以360/78°角度间隔拷贝了77次单叶片模型,建立了整圈叶片有限元模型(图6).从图6可知：整圈叶片总的单元数和节点数分别达到99 216个和115 830个.采用A nsys的Apdl语言建立了相邻叶冠间的接触单元,接触单元对的总数为78.

图6 整圈叶片的有限元模型Fig.6 Finite elementm odels of a circle of blades

图7为100%转速下整圈叶片的模态.此整圈带锯齿冠叶片考虑了叶冠之间的接触干摩擦.由图7可知,整圈叶片在振动时,出现了一条或数条沿径向均匀分布的节线,这种节线称为节径,它们呈对称分布.各个通过轮心均匀分布的节径将整圈振动分成了凸凹交替的若干部分,各个部分形如扇面故称扇形振动,也称节径振动.图7(a)、(b)、(c)和(d)中固有频率的数值分别为144.38 Hz、144.392 Hz、144.427 Hz和144.484 Hz.由此可知,随着节径数的增多,固有频率的数值也增大.由表3可知：单个叶片在100%转速下一阶模态的固有频率为139.97 H z,显然在相应模态下整圈叶片的固有频率高于单个叶片的固有频率.这是由于整圈叶片叶冠之间的接触干摩擦改变了叶片的系统刚度.

2.3 动应力分析

在考虑带锯齿冠叶片的减振特性时,需分析工作状态下叶冠的接触情况,以提取等效阻尼和等效刚度计算公式中所需要的参数.在分析中,叶冠间接触面分别采用contact 174号和target 170号单元进行划分.图8为叶冠间的接触状态.从图8可知：叶片在工作过程中,叶冠不同位置接触的情况有所不同：有处于黏着状态的,也有处于滑动状态的等.但本文的分析主要针对处于黏着状态和滑动状态的区域,提取该区域的相关参数,并由此推导得出等效刚度和等效阻尼的数值.

笔者对带锯齿冠叶片的干摩擦减振特性进行了分析,在叶片某截面的叶背处取某节点,计算了该节点在有、无干摩擦阻尼作用下的应力值.为了便于比较,定义了以下无量纲的相对应力值：

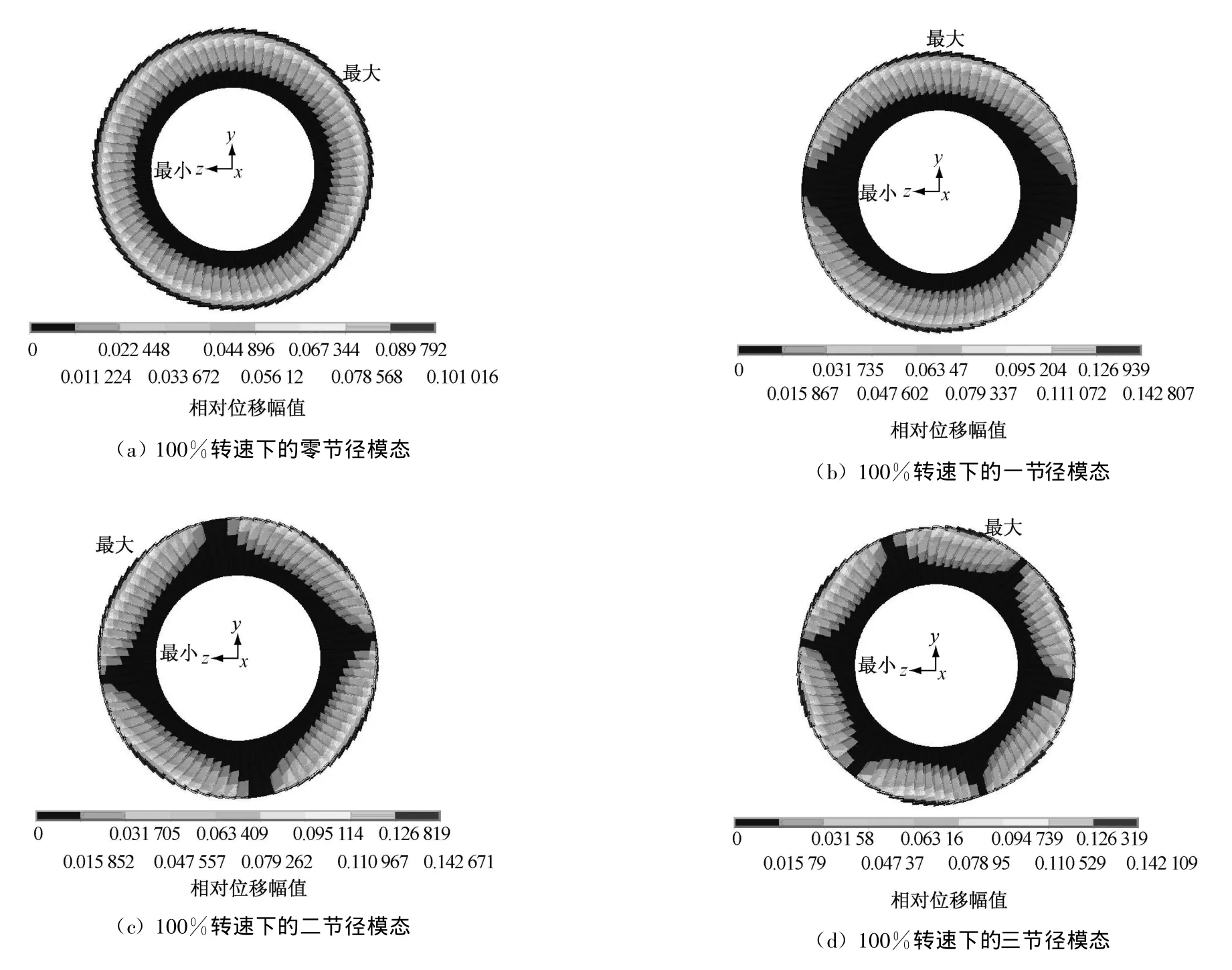
图7 100%转速下整圈叶片的模态Fig.7 M odalmap sof a circ le of bladesunder rotation speed of 100%

图8 叶冠间的接触状态Fig.8 Contact status betw een the blade shrouds

式中：σ为引入干摩擦阻尼后系统的振动应力;σ0为不考虑干摩擦阻尼、系统共振时的应力.

图9为某节点在有、无干摩擦阻尼下的动应力.从图9可看到：在考虑叶冠之间的干摩擦阻尼后,叶片在给定激振力下的动应力下降了约55%,在有、无干摩擦阻尼下的动应力均在叶片的固有频率附近达到最大值.

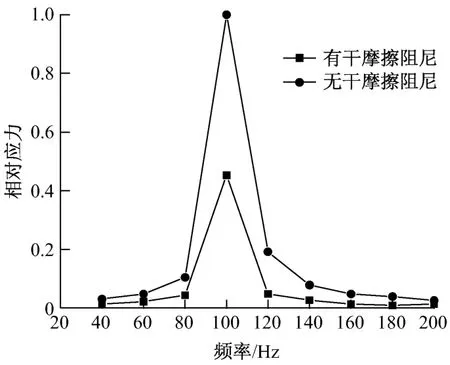
图9 某节点在有、无干摩擦下的动应力Fig.9 Dynam ic stress of one node on the blade w ith and withou t dry friction

3 结 论

(1)随着转速的提高,带锯齿冠叶片在各阶模态下的振动频率的数值也增大,单个叶片在100%转速下的一阶模态固有频率为139.97 H z,整圈叶片的一阶模态固有频率为144.38 Hz.

(2)引入“滞后”弹簧摩擦模型能较好地描述带锯齿冠叶片的干摩擦阻尼特性.

(3)采用接触单元计算了带锯齿冠叶片在工作过程中叶冠间的接触状态,提取出接触区域的摩擦力参数,并计算了其等效刚度和等效阻尼.

(4)计算了有、无干摩擦阻尼作用下带锯齿冠叶片的动应力.与不考虑叶冠之间的干摩擦阻尼相比,在考虑了叶冠之间的干摩擦阻尼后,叶片在给定激振力下的动应力下降了约55%,说明干摩擦阻尼具有明显的减振效果.

[1] 李剑钊,闻雪友,林志鸿.汽轮机带冠叶片振动特性研究进展[J].汽轮机技术,2005,47(4)：241-247.LI Jianzhao,W EN Xueyou,LIN Zhihong.The advancement of study on vibration characteristics of shrouded blade o f steam turbine[J].Turbine Technology,2005,47(4)：241-247.

[2] 赵子辉,谢永慧,张荻,等.汽轮机叶片结构阻尼研究发展现状及展望[J].汽轮机技术,2008,50(1)：1-5.ZH AO Zihui,XIE Yonghui,ZHANG Di,eta l.Review of research on damper of turbine blade[J].Turbine Technology,2008,50(1)：1-5.

[3] 谢永慧,张荻.大功率汽轮机末级叶片三维动态应力及服役寿命的研究[J].动力工程,2007,27(1)：11-15.XIE Yonghui,ZHANG Di.Study on 3-dimensional dynam ic stress and service life of large steam turbines'last stage blades[J].Journa l of Power Engineering,2007,27(1)：11-15.

[4] 张锦,刘晓平.叶轮机械振动模态分析理论及数值方法[M].北京：国防工业出版社,2001：393-394,396.