基于内模控制的水轮机调节系统的优化设计

陈亮亮，张江滨

（1.中国水电顾问集团西北勘测设计研究院，西安 710065；2.西安理工大学水利水电学院，西安 710048）

基于内模控制的水轮机调节系统的优化设计

陈亮亮1，张江滨2

（1.中国水电顾问集团西北勘测设计研究院，西安 710065；2.西安理工大学水利水电学院，西安 710048）

水轮机调节系统是一类典型的非最小相位系统，为抑制其右半复平面零点所造成的负调，提出一种采用极点镜像映射法的 IMC-PID控制和模糊逻辑设定值加权的混合策略。采用内模控制极点映射方法设计PID控制器，能够降低不稳定零点带来的负调；引入的模糊逻辑设定值加权系数可以在线修正控制器的比例增益，从结构上有效抑制负调产生。仿真结果表明，该控制器对水轮机调节系统具有良好的控制效果。

水轮机调节系统；内模控制；仿真研究

1 引言

水轮机调节系统由于水流惯性的存在，使整个系统成为一个典型的只有右半复平面零点的非最小相位系统[1]。从控制原理知道，右半复平面的正零点属于不稳定零点，由此产生的负调现象是系统控制所不希望的。

针对水轮机调节系统一类的非最小相位特点，很多学者进行过研究。基于经典控制理论的设计大都局限于线性控制器，难以同时抑制负调、超调和调整响应时间；而基于智能控制的设计方法[2]虽然也得到了研究，却因为自身的复杂性而使得实际的操作难度倍增；近年来，以预测算法、模型参考等为基础的控制方法[3-5]有了长足的发展，其中更是以内模控制[6,7]受到了大家的广泛关注。

以内模控制极点镜像映射的方法为基础，针对水轮机调节系统的非最小相位特点设计PID控制器，从而通过参数整定有效的抑制负调；并结合模糊控制技术对控制器的设定值进行加权，从系统结构上抑制负调的产生。理论分析和仿真结果均验证了该混合策略的有效性。

2 问题描述

目前，工业控制系统使用最为广泛的仍然是结构简单的经典PID控制。虽然有学者进行过基于内模控制的设计[8]，而且也取得了不错的效果。但是，将内模控制和PID控制的优点结合起来，才会更有实用价值，所以本文采用基于内模控制的PID设计方法。

内模控制器的传统设计方法很难满足非最小相位系统的需要，而水轮机调节系统正是一个典型的非最小相位系统，所以需要重新定义设计公式，故本文采用极点镜像映射法设计系统控制器。

根据经典PID设计方法，引入设定值加权系数[9]后，系统得以从结构上抑制负调的产生。但此系数的大小会影响系统响应的快速性，所以需要在系统响应过程中动态计算该值的大小。

3 混合控制策略

3.1 IMC-PID控制

内模控制的结构如图 1所示，图中 Gq（s ）为内模控制器， Gp（ s ） 为被控对象， Gm（ s）为对象模型；r、u、d、y分别为输入量、控制量、扰动量和输出量。

图1 内模控制结构

对象模型可以分解为 Gm+（ s ） 和 Gm-（ s） ，即：

其中， Gm+（ s ）为包含时滞和右平面零点的逆不稳定部分， Gm-（ s ）则为包含最小相位特征的稳定部分。

设计内模控制器时，定义内模控制器为：

其中，在稳定部分上增加的 Gf（ s ）为滤波器，用来保证内模控制器的物理可实现性，确保系统的鲁棒性。一般采用如下形式：

式中，阶次n取决于 Gm-（ s）的阶次以使控制可实现；λ为时间常数，s为拉氏算子。

由图1可知内模控制的系统输入输出特性为：

如果模型精确，即 Gp（ s ）= Gm（s ）时，系统的输出为：

显然，改变 Gq（ s）参数λ就可以分别调整系统的目标跟踪特性和干扰抑制特性。

将内模控制结构等效变换为经典PID控制结构，如图2所示，其中， Gc（ s ）为等效PID控制器。

图2 经典二自由度PID控制结构

由图2可得：

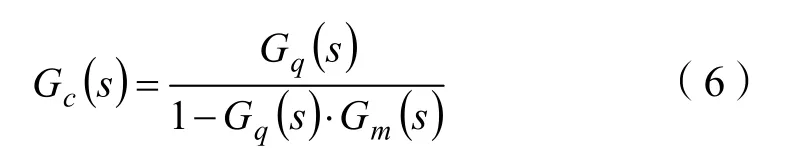
3.2 IMC-PID的参数整定

由于水轮机调节系统中电液随动系统的时间常数较小，因此，将系统的模型降为二阶，由此得到系统的对象模型 Gm（ s ） 为：

为了消除水流惯性对系统的影响，采用极点镜像映射的方法。在设计内模控制器的时候，不仅将模型的稳定部分求逆，而且添加非最小相位零点在左半平面的镜像极点。即将式（2）变为：

将式（3）和式（7）代入式（8），可得内模控制器 Gq（s ） 为：

将式（7）和式（9）代入式（6），可得等效PID控制器 Gc（ s ） 为：

将式（10）分解为常规控制（IMC-PID）和抑制负调（RU）两部分，可得水轮机调节系统的参数整定为：

3.3 模糊逻辑设定值加权

传统IMC-PID控制器在时域的标准形式为：

式中，e（ t ）为系统误差，u （ t）为控制变量，Kp、Td和 Ti分别为比例增益，微分作用系数和积分作用系数。

因为比例增益pK 的增大或减小可明显改善系统响应的超调量和调节时间，所以为了克服传统IMC-PID控制器的不足，行之有效的方法就是在控制器的比例作用部分引入设定值加权系数常量b，式（11）变为：

式中， ep（ t）= b r（t）- y （t）， b ∈ （0,1） 。即：

由式（13）能够组建改进的IMC-PID控制器，如图3所示。Go（ s ）为引入加权系数后的控制器，这样一来，系统的精度与稳定就由 Go（ s ） 和 Gc（ s ） 分别控制。

图3 改进IMC-PID控制器结构

然而，常规的加权系数b是固定的。在此条件下，当系统其他性能指标达到良好时，通常导致上升时间增大。为此，我们根据系统误差 e（ t ）和误差变化 ec（ t）模糊推理当前时刻的b值，构建出能够随系统响应过程而不断改变b值的控制器 Go（ s）。

在模糊系统中，输入 e（ t ）、 ec（ t） 和输出f的隶属度函数都限定在[-1，1]，如图4所示。模糊控制规则如表1所示，其中NVB、NB、NM、NS、ZO、PS、PM、PB、PVB分别代表负极大、负大、负中、负小、零、正小、正中、正大、正极大。

4 仿真与分析

为了验证混合策略在水轮机调节系统中的性能，使用MATLAB软件对其进行仿真。取参数 ey=0.74，eqh=0.49，e=1.07，Tw=1.62，Ta=6.67，en=1，Ty=0.1，bp=0.04；利用开环对数频率特性确定校正环节参数bt=0.49，Td=4.9；滤波器时间常数λ1=6.8，λ2=5。

从图5可以看出，采用IMC-PID控制器与采用传统PID控制器相比，系统负调得到了微小的抑制，系统超调得到了较大的抑制。

针对水轮机调节系统水流惯性的存在，采用极点镜像映射法设计IMC-PID控制器。

从图6可以看出，采用极点映射的IMC-PID控制器与未用极点映射的IMC-PID控制器相比，系统在不损失其他性能的条件下，负调得到了明显的抑制。

图4 隶属度函数

表1 模糊控制规则

图5 传统PID和IMC-PID控制器的系统阶跃响应

图6 极点映射前后的系统阶跃响应

考虑到实际工况的复杂性，我们将被控对象的时间常数和增益均增加20%。

从图 7可以看出，在模型失配的情况下，采用IMC-PID控制器与采用传统PID控制器相比，响应过程的波动更小，表现出优良的鲁棒性和对不同工况更强的适应力。

图7 不同工况下的系统阶跃响应

从图8可以看出，设定值加权系数b的选择与系统响应时间关系极大。为了更好地抑制负调，需要减小b值，但b值的减小会降低系统响应的快速性。使用模糊控制技术可以实现b值的动态计算，在系统负调较小的情况下，又能够拥有较好的响应时间。

最后将传统PID控制和采用极点映射的IMC-PID控制（PM-IMC-PID）与本文所提出的混合策略（PM-FSW-IMC-PID）作比较，得到系统的阶跃响应如图9所示。

图8 采用设定值加权的系统阶跃响应

从图 9中可以看出，混合策略同时兼顾了IMC-PID参数整定和设定值加权的优点，负调和超调都非常微小，系统响应的快速性也没有很大损失，控制品质更加优良。根据不同需要，系统通过参数调整可以获得更快的系统响应或者更强的干扰抑制。

图9 混合策略的系统阶跃响应

5 结论

仿真结果表明，混合策略针对水轮机调节系统的非最小相位特点，明显抑制其负调，使鲁棒性更加优良。通过合理的参数调整，就能够令其同时兼具良好的目标跟随特性和干扰抑制特性，改善了传统控制器的不足；模糊控制的应用，一定程度上解决了设定值加权带来的负面影响。此外，由于结构简单、调节参数少，使该策略更具实用性。

[1] 胡寿松. 自动控制原理[M]. 北京： 科学出版社，2001.

[2] 屈颖, 孙建平, 施壮. 一种用于非最小相位系统的模糊控制器设计[J]. 控制工程, 2004, 11: 25-26.

[3] 李少远, 章春利, 陈增强, 袁著祉. 非最小相位系统具有强鲁棒性的广义预测控制[J]. 控制与决策, 1998, 13(1): 63-66.

[4] 贺也平, 徐克虎, 沈春林. 非最小相位系统输出跟踪的最优预测控制方法[J]. 南京航空航天大学学报, 2000, 32(3): 263-269.

[5] 刘浩, 刘晓华, 张喜英. 非最小相位连续时间系统广义预测加权控制算法[J]. 鲁东大学学报(自然科学版), 2007, 23(2): 114-116.

[6] 鲁照权. 一类非最小相位过程内模控制系统设计[J]. 基础自动化, 2004, 9(2): 7-9.

[7] 武成烈, 吴艾, 余向阳, 吴罗长. 基于内模控制的水轮机调节器仿真研究[J]. 西北水力发电,2005, 21(4): 1-3.

[8] 宋晓燕, 王泳. 基于内模设计法的非最小相位系统控制[J]. 平顶山学院学报, 2007, 22(2): 77-80.

[9] Astrom K, Hagglund T. PID Controllers：Theory，Design and Tuning[M]. New York: ISA, 1995.

张江滨（1962-），2006年毕业于西安理工大学水文学及水资源学科专业，博士，现任西安理工大学动力系教授、副主任，兼任陕西省水力发电学会自动化专委会委员，研究方向：水利电力自动化、发电机组自动控制、电力系统运行与控制。

Optimal Design of Hydro-turbine Regulating System Based on Internal Model Control

CHEN Liang-liang1, ZHANG Jiang-bin2
( 1. Hydrochina Xibei Engineering Corporation, Xi’an 710065, China；2. Xi’an University of Technology, Xi’an 710048, China )

Hydro-turbine regulating system is a typical non-minimum phase system, for eliminate the undershoot caused by zeros in the right-half plane, a IMC-PID control and fuzzy logic set-point weight mixed strategy has been advanced. The PID controller based on the internal model control with pole mapping method, to reduce the undershoot, and the fuzzy logic set-point weight factor that can control the proportion of gain, structurally effective eliminate the undershoot. The simulation results show that the controller make hydro-turbine regulating system has good control effect.

hydro-turbine regulating system; internal model control; simulation study

TK730.4+1

A

1000-3983（2010）01-0060-05

2008-08-04

陈亮亮（1984-），2009年毕业于西安理工大学水利水电专业，硕士，现从事水利电力自动化设计工作。