基于TMS320F2812的异步电机矢量控制系统
陈顺中,谈龙成,王秋良
(中国科学院电工研究所,北京 100190)
基于TMS320F2812的异步电机矢量控制系统
陈顺中,谈龙成,王秋良
(中国科学院电工研究所,北京 100190)
传统的矢量控制方法基于异步电机的稳态模型,控制性能受电机的参数影响很大。本文结合异步电机的特性和要求在控制策略中设计了转速、电流、磁链等多个闭环,采用了对参数依赖性很小的偏差电压解耦方式,并结合电机的电压模型和电流模型对传统的转子磁链计算进行了补偿和修正,有效地降低参数变化对系统的影响。DSP芯片TMS320F2812有着强大的运算能力和优良的控制性能,基于该芯片的硬件系统很好地实现了控制方案,实验表明该控制系统精度高,实时性和动态响应都较好。
偏差电压解耦;矢量控制;转子磁链;TMS320F2812
1 引言
矢量控制的本质就是把交流电动机模拟成直流电动机来控制,通过坐标变换把定子电流矢量分解成转矩分量和励磁分量。由于两个分量是解耦的,可以分别加以控制,从而能取得与直流电机相媲美的控制性能。但矢量控制算法中大量使用了电机参数,而在运行中电机参数变化很大(如转子电阻最大变化可达50%),极大地影响了控制系统的性能。如何消除参数的变化对控制性能造成的影响成为矢量控制中的一个重要课题。
为了解决这一问题,很多学者在电机参数在线辨识方面做了大量的工作。文献[1]~[4]介绍了几种常见的电机参数在线辨识方法,主要有扩张卡尔曼滤波法(EKF)、模型参考自适应法(MRAC)、神经元网络法(ANN)等等。但这些方法算法复杂,需要大量实时计算,而且很多都包含了微分运算环节,容易产生运算结果的“毛刺”现象。文献[5]在控制环节中加入了相角闭环来补偿由于参数变化引起的转子磁链误差,但其依据电机的电流模型,在低速时补偿效果不佳。
本文根据闭环对参数变化具有抵抗作用,在控制策略中设计了转速、电流、磁链等多个闭环,电压解耦环节采用了对电机转子参数依赖性很小的偏差解耦方式,并且结合了电机的电压模型和电流模型对控制中的核心变量(转子磁链)进行了补偿和修正。绕过复杂的参数辨识环节,大大降低了电机参数变化对控制系统的影响。采用TI公司生产的DSP芯片TMS320F2812实现了该矢量控制系统的软硬件设计,取得了较好的实验结果。
2 转子磁场直接定向矢量控制原理
矢量控制有定子磁场、气隙磁场和转子磁场3种磁场定向方式。这里采用转子磁场定向,实现对定子电流的转矩分量和励磁分量的解耦。通过3/2变换和旋转变换可以得到异步电机在以转子磁链为d轴,与之垂直且超前π/2方向为q轴的旋转坐标下的数学模型[6,7]:

式中:L,R,w,ψ—— 电感、电阻、角速度和磁链;
下标s,r,m,d,q——定子、转子,磁场量旋转坐标系的d轴和q轴分量;
Tr,Te,p—— 转子时间常数,电磁转矩,微分算子;
δ——定子电感因数,δ=1-L2m/LrLs;
δr—— 转子漏磁因数,δr=Lrl/Lm。
实际控制中引入PI调节器,绕开参数对电流进行有效控制。PI调节器具体算法如下:

但从式(7)和式(8)可以看出,d 轴和q轴之间存在耦合。要消除交叉耦合量的影响必须对d、q轴电压进行解耦。目前,学者共提出3种解耦方法:反馈解耦、前馈解耦、偏差解耦[8]。本文采用偏差解耦的方法,通过电流给定信号与反馈信号的差值进行PI调解以生成耦合量:

将PI调节引入到解耦电压项的计算中,不仅保证了高速运行时系统跟随给定变化的调节能力和快速响应给定的变化,更重要是在电机运行中,转子电阻和转子电感的变化非常大,偏差解耦避开了这两个参数,增强了系统对电机参数变化的抵抗能力。
3 对转子磁链计算与控制的改进
在矢量控制中,转子磁链ψr和磁场定向角θs都是实际值,但这两个量是难以直接测量的,只能采用观测值或模型计算。传统的观测器所依据的电机模型方程为(4)~(6)。从式中可以看出,传统的转子磁链观测器依赖于电机参数的正确性,受参数变化影响很大。为了解决这个问题很多学者在电机参数在线辨识方面进行了大量的研究工作。这里对传统的转子磁链计算和控制进行改进,提出一种新的转子控制方法,从而绕过参数在线辨识,使系统在运行中不受参数变化的影响[9]。
如图1所示,在理想电机模型中,令d轴与转子磁链完全重合,此时有ψr=ψrd, ψrq=0,磁链和转矩实现完全解耦。但实际运行中,由于电机参数的变化间接导致转子磁链ψr偏离d轴,假设偏至d′轴,则与理想模型中的d 轴有一偏角△θ;磁链与转矩之间存在耦合关系,无法通过定子电流中的磁链分量和转矩分量实现分别独立控制,若在控制系统中,强迫△θ为零,则非完全解耦问题便得以解决。由图1可得:

可以解得:

上面的变量中isd,isq可由传统的坐标变换求得。sdi′,sqi′可通过实测的电流、电压值在α-β坐标系中算得。电机在α-β坐标系中的数学模型可由下列方程表示:
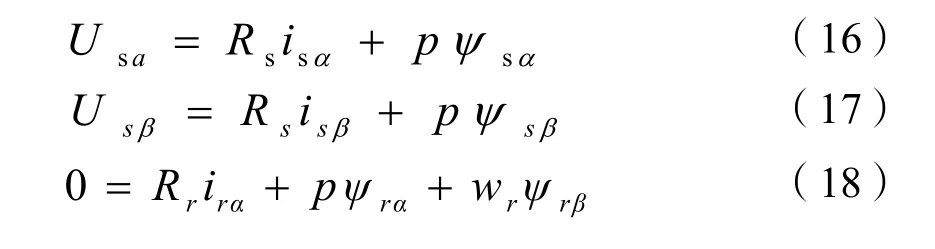


图1 异步电机转矩和磁链非完全解耦矢量图
结合图2的矢量坐标可推导出:

式中:is——定子电流的幅值;

则

通过上面方程计算出△θ,再经过一个调节器调节后将所得的值补偿到ψr给定值上来对PWM逆变器的输入电流进行调节,使△θ值等于0,从而使d’轴与理想模型中的d轴重合,实现磁链和转矩完全解耦。
4 系统控制方案
偏差电压解耦改进型矢量控制系统原理框图如图2所示。系统由一个速度闭环、一个磁链闭环、 两个电流闭环组成。

图2 偏差电压解耦改进型矢量控制原理图
5 控制系统的软硬件设计
硬件设计中采用TI公司生产的高性能数字处理芯片(DSP)TMS320F2812,该芯片是在F240X的基础上开发的32位定点处理器,主频高达150MHz,具有强大的运算能力,完全能胜任本文控制方案中的复杂算法。芯片内置了两个12位的A/D采样模块,共16个通道,为采集电机运行中的各种信号提供了方便。另外TMS320F2812还具有优良的控制能力,是一款用于电机数字控制的专用芯片,其最大特色在于内置了两个功能强大的事件管理器,其完备的功能,使得TMS320F2812几乎可以实现各种电机的控制[10]。图3以TMS320F2812为核心的控制系统示意图。
本文的矢量控制方案中包含大量复杂的数学运算,在编程时单用汇编语言来实现不仅麻烦、容易出错,而且程序的可读性和可移植性也较差,这将延长系统的开发时间并且不利于系统的维护。TMS320F2812提供了C/C++语言编译器,可用C语言进行DSP系统的开发,大大提高了开发的效率。本系统中DSP控制软件采用C语言和汇编语言混合编程的方式,汇编语言程序主要完成定时器控制、A/D采样、测速等工作,C语言程序主要完成矢量控制算法、SVPWM控制算法。主程序流程图如图4所示、图5为定时器下溢中断子程序。
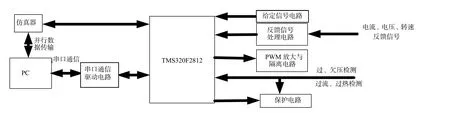
图3 控制系统硬件示意图
图4 主程序流程图

图5 定时器下溢中断子程序
6 实验结果
在实验系统平台上对本文设计的矢量控制方案进行了实验验证。实验中使用的异步交流电机参数为:额定电压Urms=460V,irms=375A,额定频率fn=50Hz,定子电阻Rs=0.015Ω,转子电阻Rr=0.01Ω,定子电感Ls=53.25mH,转子电感Lr=42.1mH,互感Lm=38.0mH,磁极对数P=1。实验结果见图8~图10。
从图6~8中可以看出,电机启动过程中转矩很快达到最大值,然后几乎保持恒定,说明电机控制中实现了恒转矩启动,而且转子磁链很快建立然后保持恒定,说明控制方案中很好实现了转矩分量和励磁分量的解耦。电机转速在启动过程中的超调量和波动都很小。图9说明电机的转速调节具有很好的动态响应性能。从图10可以看出,电机在带载稳态运行时,电压和电流波形较为理想,波形中的“毛刺”和畸变都很小,控制系统具有很好的稳态性能。

图6 电机起动过程中的转速波形

图7 电机起动过程中的转矩波形
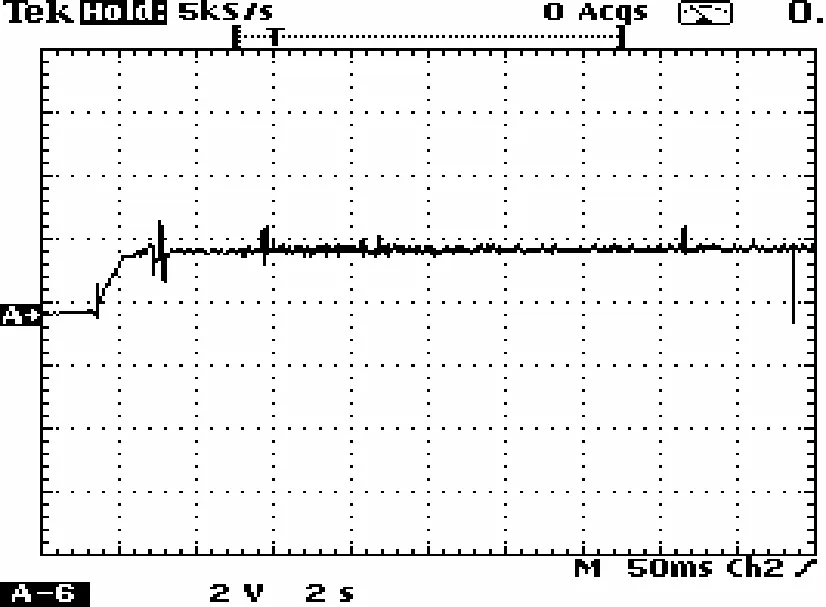
图8 电机起动过程中的转子磁链波形

图9 电机转速随给定速度响应波形

图10 带载2400r/min时电机相电压和电流波形
7 结论
本文设计的多闭环偏差电压解耦矢量控制方案有较高的控制精度,实时性和动态响应较好。DSP芯片TMS320F2812具有强大的运算能力,非常适合复杂的电机控制方案。其丰富的片内外资源,大大减少了系统的外围电路,使硬件系统更加紧凑、可靠。
[1] Samer Mayaleh, Suha Bayindir. Online estimation of rotor time constant of an induction motor using recurrent neural networks [J]. IEEE 1998. 654 -661.
[2] Nihat Inanc, Mustafa K Guven. A new sliding mode flux and speed observer for speed sensorless control of induction machine [J]. IEEE 2000. 1079-1085.
[3] Bauer F, Hming H D.Quick response space vector control for a high power three-level inverter drive system[J].EPE Aaschen 1989.417-421.
[4] Gubae Kang, Jinhwan Jung. A new rotor time constant update rule using stator flux estimates for an induction motor [J]. IEEE 1999. 500-508.
[5] 王立新, 周顺荣. 一种改进的异步电机矢量控制方法[J]. 中小型电机, 2005, 32(6): 15-17.
[6] F. Bauer, HD. Heining, Quick Response Space Vector Control for a High Power Three-levelinverter Drive System, EPE, 1989. 417-421
[7] T. H. Chin, Approaches for Vector Control of Induction Motor without Speed Sensor, IECON,1994.1616-1620.
[8] 沈滢,郝荣泰. 感应电机矢量控制解耦算法的研究[J]. 北方交通大学学报, 2003, 27(2):55-56.
[9] Jinhwan J.A Dynamic Decoupling Control Scheme for High—Speed Operation of Induction Motors[J].IEEE Trans.Industrial Electronics 1999, 46(1):100-110.
[10] Texas Instruments, “TMS320F28X System Control and Interrupts Peripheral Reference Guide”,May 2002.
Vector Control System for Asynchronous Motor Base on TMS320F2812
CHEN Shun-zhong, TAN Long-cheng, WANG Qiu-liang
(Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China)
Traditional vector control is based on steady-state model of asynchronous motor. The performance of the control system is affected greatly by motor parameters. Combining with the speciality of asynchronous motor, a number of closed loop of the rotational speed, current, and flux are designed in control strategy. Deviation voltage decoupling which depends little on parameters is adopted. Conventional calculation of rotor flux is compensated and corrected. This system effectively reduces the bad effect of the parameters variation. DSP chip TMS320F2812 has powerful operation ability and excellent control capability. The hardware system based on this chip well implements this control scheme. Experimentation indicates that this control system has the advantages of high precision, good real-time characteristics and dynamic response.
deviation voltage decoupling; vector control; rotor flux; TMS320F2812
TM346+.2
A
1000-3983(2010)01-0032-05
2008-10-10

陈顺中(1982-),硕士研究生,现从事电力电子与电力传动研究。

