机械波“半波损失”的谐波分析

徐诗池

(华东交通大学, 江西 南昌 330013)

机械波“半波损失”的谐波分析

徐诗池

(华东交通大学, 江西 南昌 330013)

利用机械波的波动方程, 分析了机械波在弦线的固定端或自由端发生反射时存在或不存在“半波损失”现象.

波动方程; 相位; 半波损失

引言

关于机械波在两种媒质分界处反射时引起的半波损失问题, 在所有大学物理教材[1～5]中都只是定性的极粗略的介绍了几句, 并没有从数学上进行证明和分析. 某些力学实验演示中出现的机械波的半波损失现象也只是给初学者以感性认识, 知其然而不知其所以然. 本短文采用谐波分析方法, 利用机械波的波动方程进行数学证明并作定量分析.

1 分析方法

设平面简谐波沿着弦线传播而从固定端或自由端反射时, 没有任何能量的吸收或发生机械波透入其它媒质, 那么, 机械波在此处是完全反射的, 反射波的振幅应该等于入射波的振幅. 在这种情况下, 边界(弦线端点)处媒质的质点, 不但参与了入射波的振动, 同时也参与了反射波的振动. 其中为角频率,为波长,是波在反射时可能发生的某一相位变化.

由于机械波的波动方程与坐标原点的选取无关, 为了简便起见, 把坐标原点取在边界上, 则边界上质点振动的合位移

现在由边界上质点振动的合位移进行分析.

(1) 当机械波反射发生在弦线固定端的分界处时, 因为该处质点不能振动, 所以振幅等于零, 即

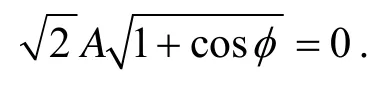
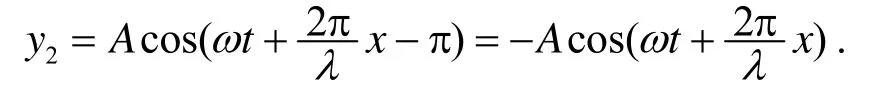
由此可知, 当机械波在弦线固定端反射时, 反射波在该处的位移要改变符号, 这说明反射波与入射波的相位在反射点正好相反, 也就表明在弦线固定端的分界处, 反射波的相位发生π的突变, 反射波的相位比入射波的相位落后π, 即存在半波损失.

(2) 当机械波反射发生在弦线自由端的分界处时, 由于自由端上的质点在一边没有受到任何运动的阻力, 该处质点较媒质内部的质点振动时受到的阻力来说就应该减少一半, 因而其振幅加倍, 即

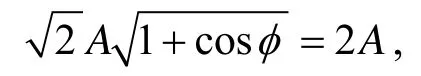
由此可见, 机械波在弦线自由端的分界处反射时, 反射波的位移在该处没有改变符号, 这表明在弦线自由端的分界处, 反射波与入射波的相位相同, 即不存在半波损失.

2 结束语

上述利用机械波的波动方程对于机械波在弦线固定端或自由端发生反射时存在或不存在“半波损失”现象所作的证明过程很容易被读者理解, 并且对于机械波传至密度和弹性模量都不相同的两种媒质分界面时, 反射波与入射波在反射点处的相位差是π或零的现象也可作出解释. 密度和波速(与媒质的弹性模量的平方根成正比)的乘积较大的媒质称为波密媒质,较小的媒质称为波疏媒质. 当机械波由较小的波疏媒质传播到较大的波密媒质的分界面上反射时, 这就相当于机械波在弦线固定端反射,反射波的相位发生的改变, 即存在半波损失. 反之, 若机械波由较大的波密媒质传播到较小的波疏媒质分界面上反射时, 这就相当于机械波在弦线自由端反射, 反射波的相位不变, 则无半波损失了.

[1] 张三慧. 大学物理学 力学 热学[M]. 北京: 清华大学出版社, 2008: 230

[2] 吴百诗. 大学物理[M]. 下册. 北京: 科学出版社, 2005: 163

[3] 徐 超, 刘修生. 大学物理[M]. 上册. 北京: 科学出版社, 2006: 124

[4] 王纪龙, 周希坚, 都虎生. 大学物理[M]. 下册. 北京: 科学出版社, 2002: 94

[5] 张丹海, 洪小达. 简明大学物理[M]. 北京: 科学出版社, 2005: 303

Harmonic Wave Analysis of “half wave loss” of the Mechanic Wave

XU Shi-chi
(East China Jiaotong University, Nanchang 330013, China )

Using the wave equation of the mechanic wave, this paper analyses the “half wave loss” phenomenon existing or non-existing when the reflection of mechanic wave at the fix end or free end of string happens.

wave equation; phase; half wave loss

O321

A

1672-5298(2010)03-0049-02

2010-05-18

徐诗池(1953- ), 男, 江西九江人, 华东交通大学基础科学学院教授. 主要研究方向: 大学物理教学