序列图像的高精度面绘制方法

刘宏,闵曙辉

(中国传媒大学信息工程学院,北京 100024)

1 引言

科学技术﹑科学仪器设备的发展,产生了大量的序列图像,如医用的 CT图像﹑ MRI图像等。在序列图像的应用初期,人们是通过阅读单个的图像,在大脑中形成所关心部分的空间位置、形状、大小信息的,这一过程需要有一定的经验,否则人脑中形成的图形和实际情况相差很大,这样就不能完整体现序列图像的价值,比如在外科手术、牙齿修复等方面的应用就受到制约。

人们应用计算机﹑数学﹑图像处理等科学技术,把所关心的等值面(灰度值相等的面)绘制出来,这样就可以形成一个三维空间的曲面,并且可以交互,极大地方便了应用。这方面最典型的绘制曲面的方法有:等高线﹑ MC算法﹑ MT算法﹑剖分立方体方法(Dividing Cubes)。在以上方法中,人们是以三角面片代替等值面,又由于是采用线性插值的方法,所以造成的误差较大。在形成三角面片时,MC算法有连接二义性问题﹑拓扑不一致性问题。

分析造成上述问题的根本原因就是在做等值面时采用线性插值的方法。体素是 MC算法中的一个重要概念.它指的是一张 CT片上某方格上的四个像素点,与另外一张 CT片上相对应方格上的四个像素点所组成的长方体。在做等值面时,首先给出等值面的灰度值,然后判断等值面与体素的每一条边是否相交,如果相交,用线性插值的方法求出交点,最后把这些交点按照一定的规则连接成三角面片,最终形成等值面。有些算法如 SMC,如果等值面与体素的某条边相交,甚至采用了取线段最大灰度值的端点为等值面所经过的点或取线段的最小灰度值的端点为等值面所经过的点,这样的方法误差会更大。本文采用在工程技术﹑计算机技术中采用的有理函数插值方法,得到了满意的结果。

2 数学基础

在数值计算里,常用的插值方法有线性插值方法﹑拉格朗日(lagrange)插值﹑哈米特(hermite)插值等。就实用的情况看,采用线性插值在三维重建中会造成伪曲面,如 CT片中的骨头的灰度值为250,而空气的灰度值为 0。给一个灰度值介于 0到250的灰度值 C,它就会在空气、骨头之间形成一个等值面。采用拉格朗日插值,由于多项式的阶数较高,插值函数 f(x)在插值点之间会产生伪扰动,这样拉格朗日插值也不能采用。哈米特插值方法除了插值多项式的阶数较高外,还必须知道插值点的导数值,这在实际应用中难以办到。

有理函数插值是在工程技术﹑计算机算法中采用的方法,它的数学模型为:

当 x=xi时, yi=f(xi) i=0,1,2,…,n+m.要找一个有理函数=f(xi), i=0,1,2,…n+m

在构造有理函数插值时,用到连分式的概念以及一些特殊记法,下面给出例子加以说明。给出有理分式用辗转相除化为连分式。

由上面把有理函数写成连分式的过程及记号方法,可以把满足 R(xi)=f(xi) i=0,1,2,…,n的有理插值函数记为:

其中 ck(k=0,1,…,n)由插值条件 R(xi)=f(xi) i=0,1,…,n确定。

下面用反差商的方法得到 ck(k=1,2,…,n+1),同时也得到了 R(x)。

定义 1 给定一组点集{xi, i=0,1,2,…},如果函数序列{vk(x)}满足如下关系

就称 vk(x)为函数 f(x)在点集{xi, i=1,2,…}上的 k阶反差商。

(舍去最后一项得)

由上可以看出,若是求出了 vi(xi),i=0,1,2,……,也就求出了 R(x)。即 f(x)的有理插值函数。求 vi(xi) i=0,1,2,……,n可以采用构造反差商表来得到。

表1

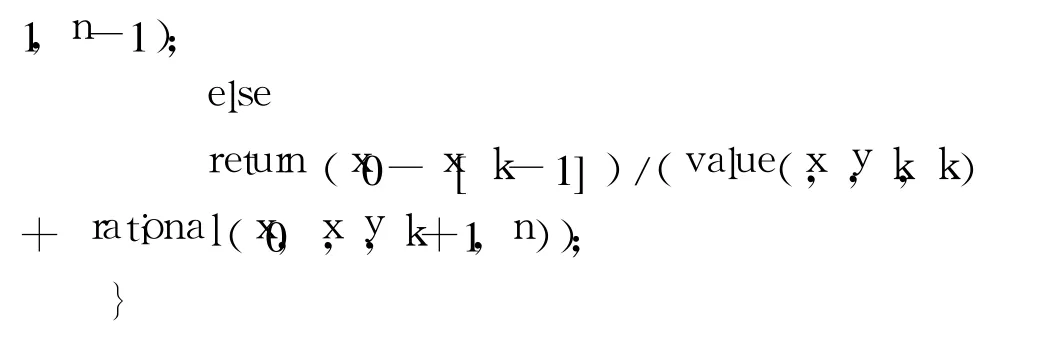
3 有理插值的程序实现

熟悉了有理插值的数学原理后,可以看出用递归方法编程实现该算法是比较可行的办法。

首先,我们需要一个函数来计算反差商表中各个值。从表 1的规律总结出以下递归函数:

double value(double x[],double y[],int k,int i){

if(k==0)return y[i];else

return(x[i]-x[k-1])/(value(x,y,k-1,i)-value(x,y,k-1,k-1));

}

下面说明一下函数的几个参数:x[]和 y[]这 2个数组分别代表进行有理插值的一组抽样点的 x坐标和 y坐标数列。k和 i与 vk(xi)=

这个函数用来计算有理插值算法产生的连分式,同样使用了递归方法,并调用了第一个函数取得反差商表中的数据。与 value函数一样,参数中的 x[]和 y[]这 2个数组分别代表进行有理插值的一组抽样点的x坐标和y坐标数列。n是指有理插值所用的抽样点个数。x0表示我们要由长度为 n的一组采样点 x[]和y[]通过有理插值得到横坐标为 x0处的估计纵坐标。这时,有理插值得到的纵坐标用 y0=value(x,y,0,0)+rational(x0,x,y,1,n)来表示。

有了有理插值的程序实现方法,下面就通过一个简单的函数来简单测试该算法的性能:

对于对数函数 ln(x+1),在区间[0,1]内等距离插入四个点,分别求出 ln(x+1)、线性插值、有理函数插值在各个插值点中间的值,可以看出有理函数插值的精度是线性插值精度的一万多倍。比如 ln(x+1)的精确值为 0.0953098,线性插值的函数值为0.0911608,有理函数插值的函数值为0.0953098.线性插值的绝对误差是 0.0041494,有理函数插值的绝对误差是 3.53e-0.07。有理函数插值的精度是线性插值精度的 11753.6倍。

在同一个坐标中画出 ln(x+1)的图像以及 ln(x+1)的有理插值﹑线性插值函数的图像,可以看出,有理插值函数的图像是和 ln(x+1)的图像是重合的。如图 1所示。中的 k和 i这 2个下标是对应的。从反差分表中可以看到,当 k为 0时,也就是第一列数值,就等于 y[]数组相应的值。

另外还需要一个函数来计算有理插值计算出来的值。

图 1 ln(x+1)和它的线性插值函数、有理函数插值函数的图像

4 高精度的曲面绘制方法

选取一系列 CT断层图像,输入这些图像数据,由于原始数据可能有噪声,所以先将原始数据经过2次中值滤波,并把这些处理后的数据存放在一个数组里。CT断层图像的灰度值是标量数据,数据类型是浮点型的。

以往的曲面绘制方法是在给出一个灰度值后判断等值面与每一个体素的每一条边是否相交,如果相交,用线性插值的方法找到等值面与体素的交点,然后用三角面片来近似代替等值面。高精度的曲面绘制方法是:给出一个等值面的灰度值 c0,先在每一张 CT片中找到灰度值为 c0的若干个点,用点列{(xi,yj,zij)}i=1,2,…,n;j=1,2,…,m表示,其中{(xi,yj,zi1)}ni=1表示从第一张 CT片中取出的灰度值为 c0的点列,其它的可类推。

对于每一个点列{(xi,yj,zij)}ni=1,过这个点列,用有理插值函数 R(x)来逼近这条等高线,用 Jj(j=1,2,…,m)表示。同样地,对于点列 {(xi,yj,zij)}mi=1,过这个点列,用有理插值函数 R(x)来逼近这一等高线,用 wj(j=1,2,…,n)表示。在三维空间中,把这两组等高线画出来,就可以得到等值面的近似曲面。

下面两个图像,分别是用高精度面绘制方法得到的皮肤表面和用 MC算法得到的等值面。从图像的效果看,高精度面绘制的曲面网能够很好地贴合皮肤,视觉效果也十分满意。如图 2和图 3所示。

图2 高精度面绘制的头部皮肤的效果图

图3 MC算法绘制的头部皮肤的效果图

需要特别强调的是在寻找灰度值为 c0的点(x0,y0,z0)时,程序判断[f(x0,y,z0)-c0]×[f(x0,y+1,z0)-c0]≦ 0是否成立,其中 f(x0,y,z0)是图像在点(x0,y,z0)的灰度值,如果成立,说明灰度值为c0的点就落在(x0,y,z0)与(x0,y+1,z0)之间。由于这两点之间的距离很小,所以用线性插值的方法寻找 y0。令y+k。

5 总结

有理函数插值算法是一种非常精确的曲线拟合算法,尤其当实际曲线比较接近一些理想数学函数时,通过有理函数插值可以由较少的抽样点拟合出精确度很高的曲线。将其用于医学图像三维重建不会产生传统 MC算法容易引起的连接二义性问题,同时又能绘制出精确度较高的表面,其误差也远远小于传统使用的线性插值算法,而且拟合出的曲线更加美观﹑光滑、自然。根据有理函数插值算法的以上特点,该方法不仅仅可以用于医学图像,而且也可以在其他研究方面得到广泛的应用,如表面设计,工业器件三维图像重建等。

[1] Burden R L,Faires J D.数值分析(第七版影印版)[M].北京:高等教育出版社,2001.

[2] 朱恒军,杨莘元.边缘检测技术在 CT图像预处理中的应用[J].哈尔滨大学学报,2007,23(1).

[3] 陈秦玉 .人体三维重建的实践和技术研究[C].浙江大学博士学位论文,2004.

[4] 罗朝东.面向有封闭内腔和外形的复杂工件快速原型制造的 ICT图像处理及反求工程研究[C].重庆大学硕士学位论文,2006.

[5] 安洪振,刘金汇.用于工业 CT图像三维重建的边缘信息提取算法研究[J].核电子学与探测技术,2007,27(5).

[6] 李庆扬,关治,白峰杉.数值计算原理[M].北京:清华大学出版社,2000.