分层空时码的译码性能仿真

杨阳,周哲

(1.北京歌华有线网络股份有限公司,北京 100007;2.中国传媒大学,北京 100024)

1 引言

分层空时结构[1]最初由朗讯公司贝尔实验室的G.J.Foschini1996年提出,称为 BLAST(Bell Layered Space-Time Architecture),并于 1998年研制出了实验系统V-BLAST,申请了专利。它需要在发射端和接收端使用多个天线(接收端天线数不少于发射端天线数目),并且在译码时需要知道精确的信道信息。本文就是重点对不同的译码方法的性能进行比较与分析。

2 分层空时结构的原理

分层空时结构其本思想如图 1所示,高速信息流先被解复用地分成多个单独的低速数据支流[1]。各个支路数据分别用各自的信道编码器编码,输出再经过分层空时结构编码和调制后送至各个独立的发射天线,接收端接收后分离混合的信号,进行译码恢复原信号。

3 分层空时结构的译码过程

3.1 译码流程

它们的数据分配如表 1所示,标识符号 a到 d表示分配到图表中的 4个发射天线的数据。在接收端,一般按照对角线数据流层进行译码,这要经过 2个步骤的处理[2]:

(1)干扰信号及未检测信号的迫零(ZF)消除。

(2)已检测信号的干扰消除和补偿。

图 1 分层空时编码的实现

前端首先使用一个空间波束形成或者迫零处理,从而分开各个单独的数据流层。例如,对 DLST的数据流层 a的求解[3]是求解 t+3时刻的流层 a的相应元素,这时利用干扰抑制方法抑制掉 t+3时刻该元素上面的数据流层 d,c,b的相应元素的影响,得到该元素的估值。然后是求解 t+2时刻的流层 a的相应元素,同样该元素上面的数据流层 d,c的相应元素的影响可以利用干扰抑制方法抑制掉,而其下方数据流层 b在 t+2时刻的相应元素则因为按照对角分层的次序译码已经得到,其影响可以通过判决反馈得到抵消。于是,可以得到 t+2时刻的数据流层 a的相应元素。如此进行下去,就可以恢复出数据流层 a。然后再用相同的方法恢复出数据流层 d,如此得到 DLST的数据层估值,再把它们送入各自的解码器,各解码器的输出再经过分层空时结构的逆变换和复用后重构出原始信息比特流的估计。

表1 对角分层空时结构 DLST的数据分配

3.2 仿真模型流程

通过设定菜单获得绘图参数→通过句柄函数确定发端信源矩阵与发射天线数→通过句柄函数确定QPSK调制→通过句柄函数确定快衰落 Raylaigh信道→通过句柄函数循环调用四种译码检测并对接收机误比特率性能进行比较→用 MATLAB仿真作图。

3.3 仿真条件设置与结行分析

现在就不同的译码对分层空时码进行仿真,通过用 ZF,ZF-SIC,MMSE,MMSE-SIC等几种译码算法仿真之后的结果性能进行比较。

仿真条件:

(1)信源随机产生。

(2)图 2收发天线数都为 2x2,图 3收发天线数都为 6x6。

图2 2x2不同译码方法的仿真图比较

(3)建立 Eb/N0与 SNR之间的换算关系:SNR=Eb/N0-10*log10(Ts*B);B=40000;Ts=1/40000;

图 3 6x6编码不同译码方法的仿真图比较

(4)在相同收发天线数的系统下进行,假设信道为独立同分布瑞利衰落信道,添加高斯白噪声,且每个用户的发射功率相等。

(5)仿真采用 QPSK调制。

(6)用 ZF,ZF-SIC,MMSE,MMSE-SIC方法分别进行译码。

(7)采用干扰抵消算法。

(8)在不同信噪比下计算 ZF接收机误比特率,以下是 ZF、ZF-SIC、MMSE、MMSE-SIC四种检测算法的性能比较。

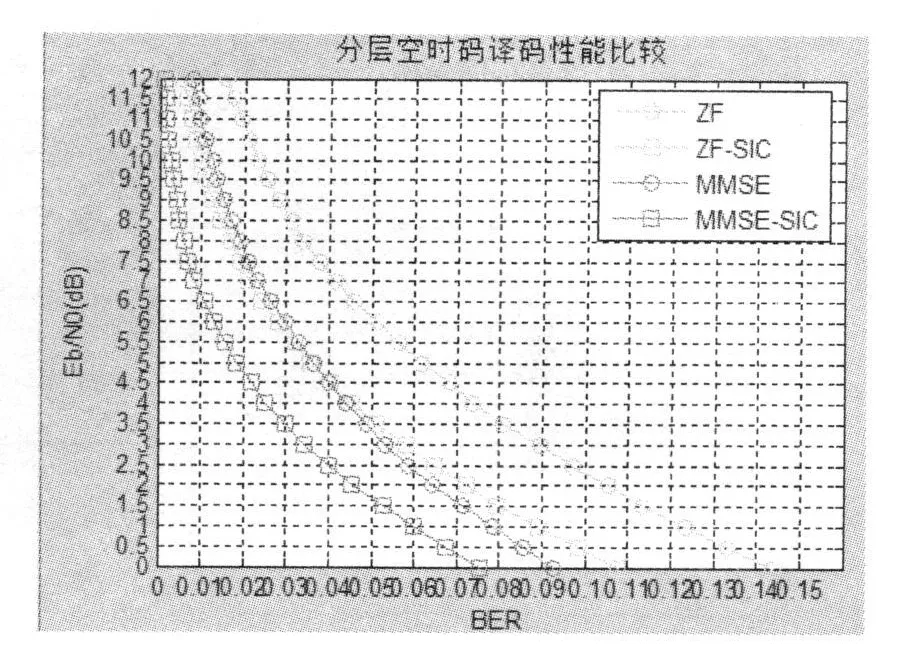
图4 2x2不同译码方法的仿真图比较

3.4 仿真结果分析:

由仿真结果可得:到在不同的信噪比下,相对应的误比特率的值,这里,我们采的 Eb/N0(我们也可以看成是信噪比,因为由 SNR=EbN0-10*log10(Ts*B);B=40000;Ts=1/40000;可知:SNR与SNR是相等的,下面用 SNR来表示)点是 0,2,4,6,8,10,12,同时在这些点取得的四种译码方法的误比特率如表所示:

表 2 不同译码方法的数值结果(对应图 2)

表 3 不同译码方法的数值结果(对应图 3)

由图 2,与表 2,可以看出 Eb/N0的值。我们知道在信噪比一样的情况下,ZF与 ZF-SIC相差比较大,后者明显强于前者的译码效果;MMSE与 MMSE-SIC相比较也达到了这样的效果,说明:SIC减小了噪音的影响,提高了译码性能。

ZF与 MMSE比较时,在信噪比一样的情况下,MMSE的效果明显优于 ZF,说明:MMSE是优于 ZF的译码方法,这也符合了复杂的译码算法,往往具有更高的译码能力。

图 2与图 3是系统在发射,接收天线数不同时,相同的环境下得出的结果。通过比较表 2与表 3,在相同的信噪比之下,表 3的数据明显比表 2的数据小,及误码率小,得知:在相同的环境下,收发天线的数目增加,译码的误码率就相应的减少,译码的效果愈好。

与图 2,图 3的变化趋势来看,ZF-SIC与MMSE的译码效果类似,只是随着信噪比的加大,(这里空间有限,信噪比只取值到 12,在试验中,信噪比范围加大到 ＞20后)MMSE比 ZF-SIC的优势会显现出来。

图 4与图 2全是在 2x2下进行的仿真,只是横纵坐标调换,坐标间隔减小,这样有助于我们的对其译码性能进行更加精确的分析:

由图 4可知,当误码率取 0.01时,MMSE-SIC与 MMSE的信噪比分别为 6.5dB,11d B,所以,MMSE-SIC比 MMSE低 4.5dB的增益。当误码率取到 0.02时,MMSE-SIC与 MMSE的信噪比分别为 4.5dB,7.5dB,所以,MMSE-SIC比 MMSE低了3dB的增益。当误码率取到 0.06时 MMSE-SIC与MMSE的信噪比分别为 1dB,2.5dB,所以,MMSESIC比 MMSE低了 1.5dB的增益。可知,MMSESIC与 MMSE比较中,SIC在低信噪比中发挥的作用越明显。

当误码率取 0.02时,MMSE与 ZF的信噪比分别为 7.5dB,10.5dB,所以,MMSE比 ZF低 3dB的增益。当误码率取 0.04时,MMSE与 ZF的信噪比分别为 4.5dB,7.25dB,所以,MMSE比 ZF低 2.75dB的增益。当误码率取 0.08时,MMSE与 ZF的信噪比分别为 1dB,4d B,所以,MMSE比 ZF低 3dB的增益。可知,MMSE与 ZF比较中,两个不同的译码方法在信噪比变化中发挥的作用相对稳定。

4 结论

误码性能的优劣顺序为 MMSE-SIC、ZF-SIC、MMSE、ZF。从而得到的结论如下:不同的检测算法,是否用串行干扰抵消算法,对性能会产生不同的影响。

ZF接收机以噪声的增加为代价抵消了不同天线间的干扰,分离了不同的数据流,MMSE接收机平衡了天线间干扰抵消和噪声增强,使总的误差最小。收发天线相同时,MMSE的性能优于 ZF,其算法的复杂度也相对较高。干扰抵消算法检测出信噪比最大的子流,减小它对其他子流的影响。干扰抵消检测减小了噪声的影响,增加了检测的分集度,从而总体的译码效果增加。

性能的提高以计算复杂度为代价,在发射天线数等于接收天线数时,计算复杂度与天线数呈线性增长关系。业已证明,对 N个发射天线和 N个接收天线的情况,系统容量随线性增长,当采用的天线个数 N=8时,在 1%的中断概率和 21dB信噪比条件下的系统的频谱利用率为 42b/(s◦Hz-1)约为相同发射功率和带宽的单发单收系统的 40倍。随着接收天线数的增加及信噪比的升高,此时分集增益的译码算法对系统性能的影响超过干扰抵消算法的影响。

[1] Siavash M Alamouti.A Transmit Diversity Technique for Wireless Communications[J].IEEE J Select Areas Communication,1998,16:1451-1458.

[2] Branka Vucetic,Jinhong Yuan.空时编码技术[M].王晓燕,译 .北京:机械工程出版社,2004.1-60,220-230.

[3] 李颖,李佳,王新梅.空时编码技术[J].西安:西安电子科技大学学报,2002,25(8):5-10.