基于声压-振速测量的平面近场声全息实验研究*
毕传兴 张永斌 徐 亮 陈心昭
(合肥工业大学噪声振动工程研究所,合肥 230009)
基于声压-振速测量的平面近场声全息实验研究*
毕传兴†张永斌 徐 亮 陈心昭
(合肥工业大学噪声振动工程研究所,合肥 230009)
(2009年5月6日收到;2009年5月31日收到修改稿)
常规的近场声全息均是采用全息面声压或质点振速作为输入量求解,由于采用单一输入量无法分离来自全息面背向声波的干扰,因此要求所有声源均位于全息面的同一侧,即测量声场为自由声场,这种要求大大限制了近场声全息的实际应用.基于声压-速度测量的近场声全息以全息面上声压和质点振速同时作为输入量,通过建立和求解两侧声源在全息面上的声压和质点振速耦合关系,可以实现全息面两侧声波的分离,从而解决上述问题.文中在前期对声场分离技术研究的基础上,基于欧拉公式和有限差分近似,推导了新的基于声压-速度测量的平面近场声全息理论公式.随后通过实验检验了该方法在有背景源干扰情况下实现声场分离和重建的有效性.
近场声全息,声场分离,声场重建,声源识别
PACC:4320,4363
1.引言
近场声全息(NAH)技术是20世纪80年代发展起来的一种具有强大的噪声源识别定位、声场计算及可视化功能的声学前沿技术.它通过测量声源近场全息面上的复声压或质点振速,借空间声场变换算法可以重建出声源表面声压、法向振速和整个三维声场中任意点处的声压、质点振速、有功声强以及声源辐射声功率等声学量[1].由于NAH技术利用了包含丰富声源细节信息的倏逝波成分,其重建分辨率大大提高,从而可以对噪声源进行识别和精确定位,也可以对声源在声场空间中的辐射属性进行预测,为噪声控制、低噪声设计等提供依据.经过近三十年的发展,相继出现了基于二维空间Fourier变换法(SFT)[1,2]、边界元法(BEM)[3,4]、Helmholtz最小二乘法(HELS)[5,6]、统计最优方法(SONAH)[7]、等效源法(ES M)[8,9]等的NAH技术,并有商业化的软件出现.
常规的NAH要求所有声源均位于全息面的同一侧,测量声场为自由声场或全息面足够靠近目标声源以至于外界的干扰可以忽略.这种要求大大地限制了NAH技术的应用.在实际测量时,通常会遇到全息面另一侧存在相干声源,或是全息面的一侧存在反射或散射.如果此时采用常规的NAH进行重建,势必会出现虚假声源,或出现较大的重建误差.
为了解决NAH的背向噪声干扰问题,于飞等[10,11]最早提出将声场分离技术应用于NAH,该方法采用Tamura等[12]提出的声场分离技术将NAH测量过程中全息面上来自目标声源辐射声从包含有背向噪声的声场中分离出来,再采用常规的NAH实施重建;在文献[13]中提出通过测量单个全息面声压和质点速度的方法来分离全息面上来自背向的噪声.李卫兵等[14]在Hald等提出的SONAH技术的基础上,提出采用基于SONAH技术的双全息面声场分离技术来分离背向噪声的干扰.最近, Hald[15]还提出一种基于双全息面声压测量的统计最优Patch近场声全息,他将该方法用于实现汽车内部声场的重建,并取得较好的效果.Jacobsen等[16]在Hald提出的方法的基础上,提出了基于声压和振速测量的SONAH技术,并与Hald提出的双面方法进行了比较[17].此外,Langrenne等[18]和Valdivia等[19]提出一种基于BEM的双面声场分离方法,毕传兴等[20]提出了一种基于ES M的双面声场分离方法,这些成果使声场分离技术可以用于任意形状声源分析.声场分离技术在NAH中非常有用,它解决了全息面背向有噪声干扰情况下的NAH重建问题,为NAH的实际应用推广提供了重要解决手段.
本文在前期对声场分离技术研究的基础上,基于欧拉公式和有限差分近似,建立新的基于声压-振速测量的平面NAH理论公式.随后以实际音箱声源为对象开展实验研究,并通过对采用本文方法分离和重建所得结果与实际结果的比较检验该方法的有效性.
2.平面近场声全息基本原理
由理想流体媒质中小振幅声波的波动方程,可以得到不依赖于时间的时谐声波场的Helmholtz方程为
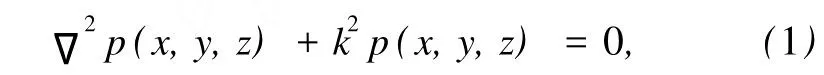
式中,p(x,y,z)为空间点(x,y,z)的复声压;k=ω/c =2π/λ为波数,c为声速,λ为波长.对于z>0的空间为自由声场的情况,即所有声源均位于z=0平面一侧,由格林公式可以得到方程(1)的解,即任意平面z上的声压同边界平面z=0上的声压、法向质点振速在波数域内的关系为

式中,ρ为声介质的密度,P(kx,ky,z)和P(kx,ky)分别为面z和面z=0上声压的二维空间Fourier变换,V(kx,ky)为在源平面z=0上波数域内的法向质点振速,kx和ky分别对应直角坐标x和y的空间频率,而kz为

对于基于声压测量的NAH,对应全息面z=zH和重建面z=zS,由(2)和(3)式可得重建基本公式为

对于基于质点振速测量的NAH,由(4)和(5)式可得重建基本公式为
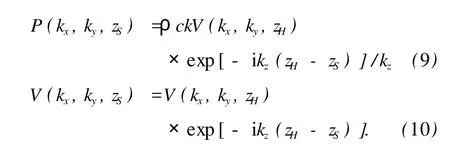
对重建获得的P(kx,ky,zS)和V(kx,ky,zS)进行二维空间Fourier逆变换,即可获得重建面上的声压、质点振速以及有功声强等声学量.
无论是基于声压还是基于质点振速测量的NAH均要求所有声源均位于全息面的同一侧,即测量声场为自由声场.如果全息面两侧都有声源,或是测量面的一侧存在反射等,此时再采用常规的NAH进行重建,势必会出现虚假声源,或出现较大的重建误差.而基于声压-速度测量的NAH则很好地解决了该问题.
3.基于声压-速度测量的平面近场声全息原理
图1为全息面与源面之间的空间位置关系:全息面H两侧均有声源,其中全息面与坐标平面(x, y)重合,即zH=0.两侧源面均与全息面平行,源面S1代替目标声源,源面S2代替来自全息面背向的干扰声源.

图1 全息面与声源之间的位置关系
对于稳态声场,全息面H上任意点(x,y)的复声压p(x,y)为两侧声源辐射声压的叠加,即
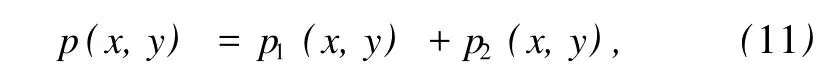
式中,p1(x,y)为目标声源在点(x,y)处产生的声压;p2(x,y)为干扰声源在该点产生的声压.同样,该点的法向振速v(x,y)为
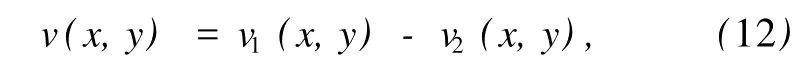
式中,v1(x,y)为目标声源在该点引起的法向质点振速;v2(x,y)为干扰声源在该点引起的法向质点振速,目标声源和干扰声源在全息面上的法向质点振速方向相反.
在实际应用中,(12)式中法向质点振速v(x,y)很难直接测量获得.但可以通过在全息面附近布置一辅助测量面,由有限差分近似计算获得.根据Euler公式,全息面上任意点(x,y)的法向质点振速为

设辅助测量面H′上任意点(x,y)的复声压为p′(x,y),则可得全息面上的法向质点振速为

将(14)式代入(12)式,并对(11),(12)式两边分别取二维空间Fourier变换,可以得到波数域内该全息面上各声压和质点振速之间的关系为
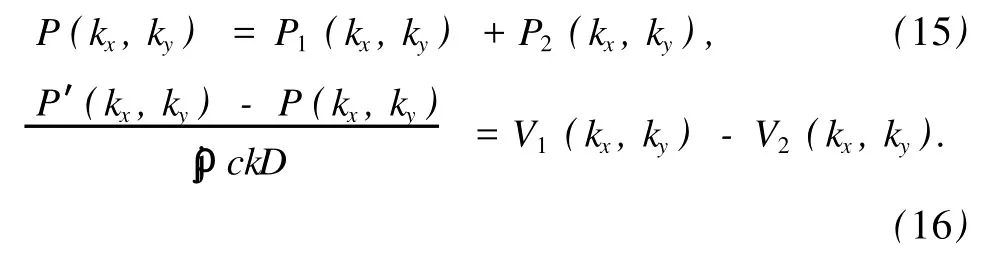
对于目标声源和干扰声源辐射声压和质点振速之间的关系同样可以用Euler公式表示,在波数域内,两声压和法向质点振速之间关系分别为
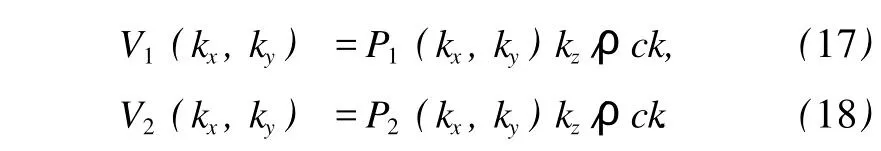
将(17)和(18)式代入(16)式,并联合(15)式,可以解得目标声源在全息面上单独产生的声压为

将(19)式代入(17)式,可得目标声源在全息面上单独产生的法向质点振速为
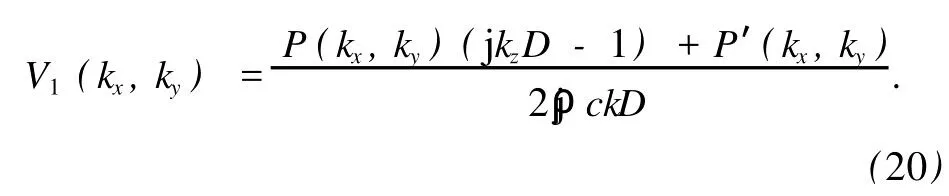
将(19)式分离的波数域声压代入(7)和(8)式,则重建出目标声源在源面S1上的声压和法向质点振速分别为

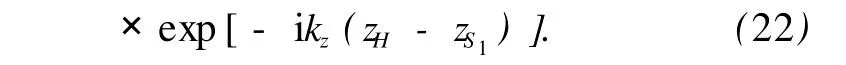
将(20)式分离的波数域质点振速代入(9)和(10)式,可以得到(21)和(22)式相同的重建公式.由于采用分离的声压和质点振速重建的结果相同,因此本文只讨论采用分离的声压重建情况.
对(21)和(22)式取二维空间Fourier逆变换,则可得到目标声源在源面S1上的空间域复声压和质点振速,进而可以获得有功声强等其他声学参量.
4.实验研究
为了验证建立的基于声压-振速测量的平面NAH理论公式的有效性,本文选取两个音箱声源作为研究对象,并对采用本文方法分离和重建所得结果与实际结果进行比较.
实验是在如图2所示半消声室中完成的,半消声室的本地噪声为16 dBA.实验声源为分布在全息面两侧的两音箱源,其中一个为目标声源,另一个为干扰声源.声源信号为信号发生器产生的700 Hz信号,经步步高AV220声频功率放大器放大后,分别输入两音箱所产生.测量采集装置为成都中科IDTS-4516U型16通道数据采集器,以及北京声望技术公司的MP201系列前置放大器、1/2英寸压电传声器和BS WA MC1116型号信号调理器.

图2 实验装置实物图
实验选取的全息面、辅助测量面与源面之间的位置关系如图3所示.全息面H为平行于音箱前表面的1 m×0.7 m的平面,全息面上均匀地分布有21×15个测点,全息面与源面S1的距离为0.125 m,与源面S2的距离为0.225 m.辅助测量面H′与全息面H之间的距离为0.075 m.目标声源的音箱纸盆中心坐标为(0.0 m,-0.15 m,-0.125 m),干扰声源的音箱纸盆中心坐标位于(0.0 m, 0.15 m,0.225 m).

图3 测量面与声源位置关系图
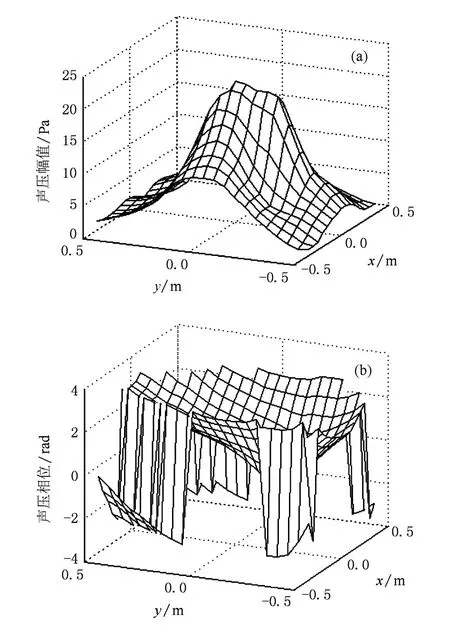
图4 测得的全息面上声压幅值与相位 (a)声压幅值,(b)声压相位
全息面H和辅助测量面H′上各测点处的声压由1个参考传声器和11个测量传声器组成的阵列逐列扫描获得.两测量面上的声压幅值由各传声器采集的信号做自谱获得,其相位通过求取测量传声器采集信号与参考传声器同步采集信号的相位差获得.在全息面和辅助测量面声压测量过程中,参考传声器位置始终固定不变.测量所得全息面H上复声压的幅值和相位分布如图4所示,借助辅助测量面测量所得到全息面H上的质点振速的幅值和相位分布如图5所示.为了比较本文方法分离和重建的效果,实验还需测量移除干扰源后,目标源单独发声时全息面上复声压,测量结果如图6所示.比较图4和6可以看出,未移除干扰源测量的声压与测量的目标源单独辐射声压存在明显差异.

图5 测得的全息面上质点振速幅值与相位 (a)质点振速幅值,(b)质点振速相位
为了进一步量化分离和重建的效果,定义误差为
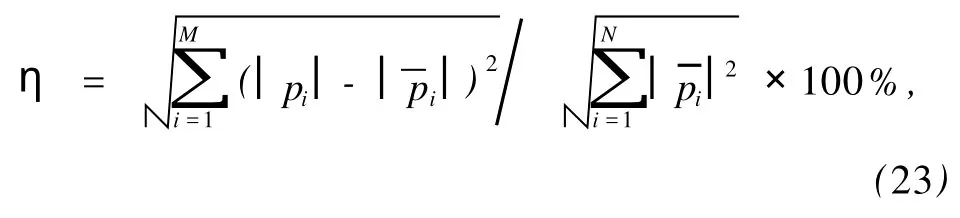
式中,N是测量点数,pi为测量面上第i点处声压值,¯pi为测量面上第i点处目标源单独辐射声压值.
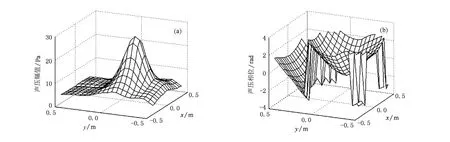
图6 目标声源单独发声时,测得的全息面上声压幅值与相位 (a)声压幅值,(b)声压相位
按(23)式定义误差,未移除干扰源测量的声压误差达到39.35%,显然此时全息面声压已被干扰源严重污染,采用该全息数据直接重建目标声源势必会出现虚假声源,使重建结果出现较大偏差.下面将采用本文方法实施分离,检验本文方法分离和重建结果的有效性.

图7 分离的目标声源在全息面上产生的声压幅值与相位 (a)声压幅值,(b)声压相位
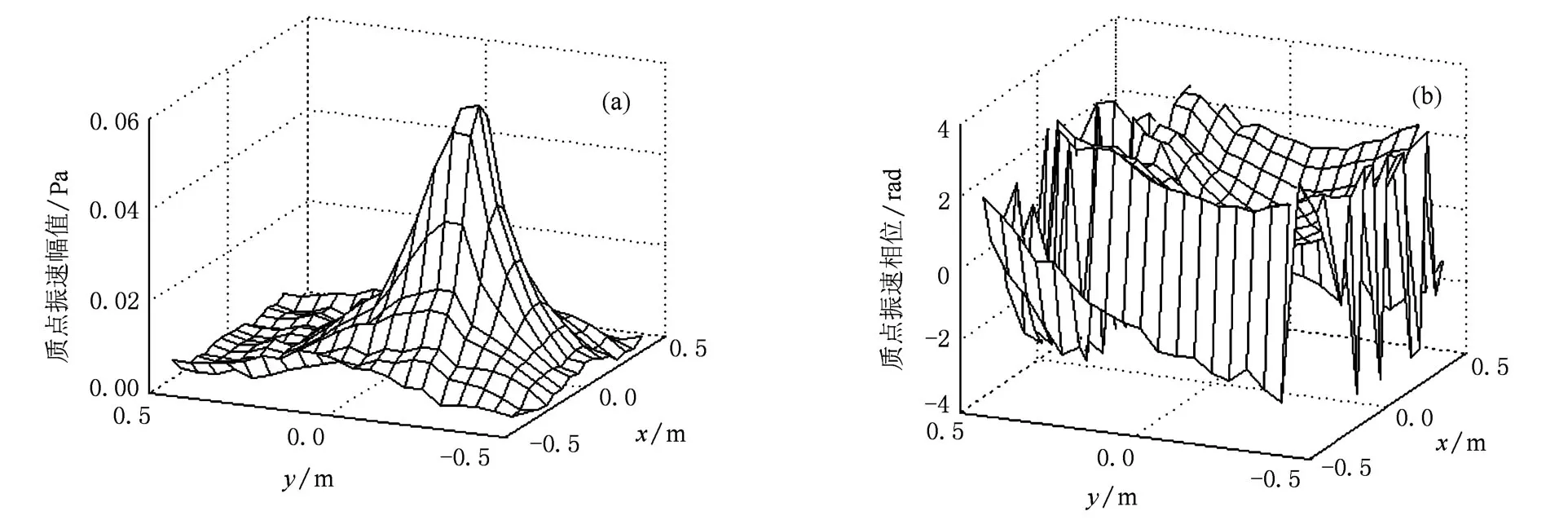
图8 分离的目标声源在全息面上产生的质点振速幅值与相位 (a)质点振速幅值,(b)质点振速相位
由于本文在实施分离和重建过程中均是基于二维空间Fourier变换方法,受到离散化和测量孔径大小的限制,会给分离和重建带来混叠误差和卷绕误差.本文在声场分离和重建过程中通过在全息面四周补零,使全息面孔径扩展,从而减小卷绕误差的影响.利用补零后的全息面和辅助测量面上的声压,通过声场分离公式(19)和(20)计算目标声源在全息面上产生的声压和质点振速分别如图7和8所示.从图7和8可以看出,采用本文方法可以有效实现全息面两侧声源的分离,实施分离后,所获得的声压和质点振速已基本消除干扰源的影响,分离出的声压与图6所示目标源单独辐射声压基本一致.图9为抽出全息面的一行(y=0)声压与相应的未分离前的声压,以及目标声源单独在该全息面上产生的声压实测值的比较,图示结果更清晰地说明了分离的效果.按(23)式定义误差,分离声压的误差为14.87%.显然,实施分离后显著降低了声压误差,从而为进一步进行目标声源重建提供了可靠的全息数据.
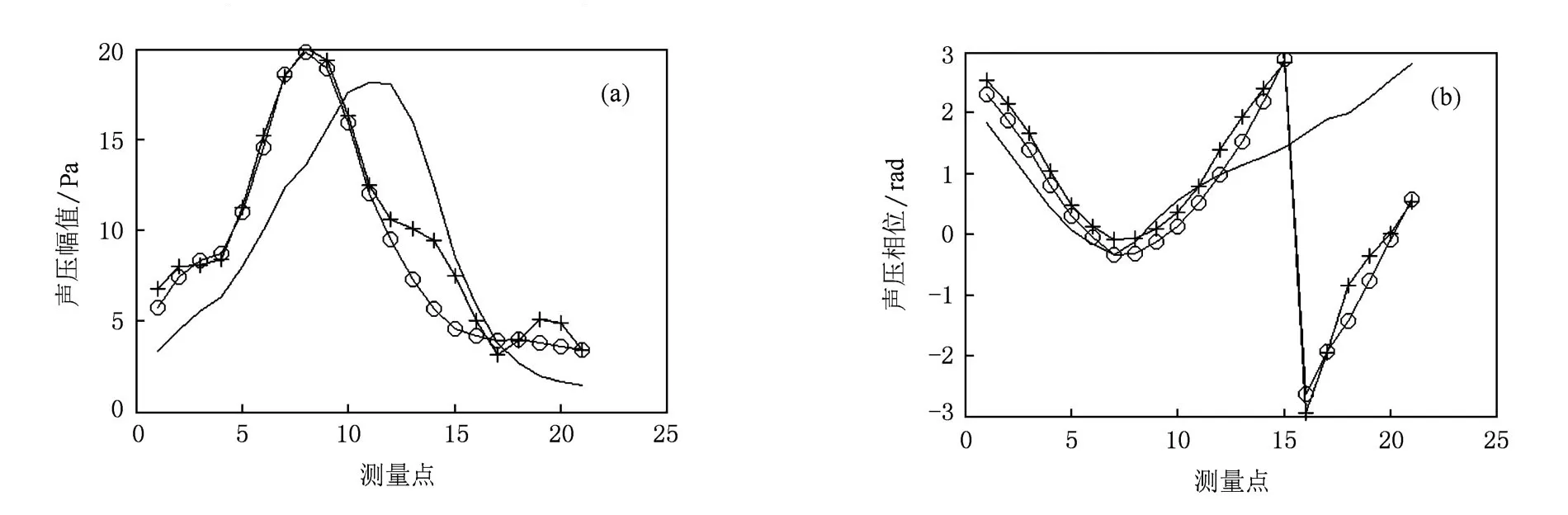
图9 全息面上中间一行分离前、后声压幅值和相位比较 实线为未分离实测值,+为分离后结果,o为实测目标声源辐射声压. (a)声压幅值,(b)声压相位
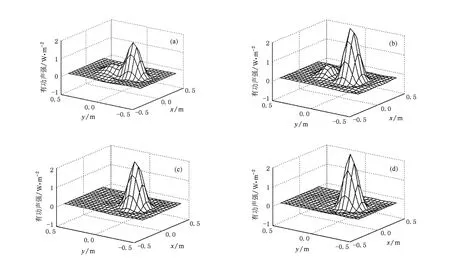
图10 重建源面S1上有功声强分布情况 (a)采用未分离的声压重建的结果,(b)采用未分离的质点振速重建的结果,(c)采用分离的声压重建的结果,(d)移去干扰声源后采用目标声源单独辐射声压直接重建的结果
利用分离后的全息声压和质点振速可以重建源面S1上的有功声强.图10(a)为直接利用全息面上带有背景干扰的声压数据重建源面上的有功声强结果,在图中出现两个声源,其中一个是目标声源,而另一个正是干扰声源影响所产生的伪声源.在实际工程应用中,该结果将可能误导研究人员作出错误的判断.图10(b)为直接利用全息面上带有背景干扰的质点振速数据重建源面上的有功声强结果,在图中同样出现了伪声源.图10(c)为利用分离后全息面上的声压数据重建源面上的有功声强结果,显然重建结果准确地指出了目标声源的位置,很好地去除了干扰声源对全息重建结果的影响.图10(d)为利用测量的全息面上目标声源单独辐射的声压数据重建源面上的有功声强结果.比较图10(a),(b),(c)和(d)可知,采用未分离的声压或质点振速数据重建均会出现虚假声源,而采用分离后的全息声压重建则有效排除了干扰声源对全息重建结果的影响,重建结果几乎可以达到直接移去干扰声源后重建的效果.按(23)式相同的误差定义方式,采用全息面未分离的声压重建的声强误差为33.96%,采用全息面未分离的质点振速重建的声强误差为35.52%,而采用分离的声压重建的声强误差仅为15.16%.以上实验结果验证了本文方法的有效性.该方法的采用为近场声全息技术在实际工业环境下应用提供了解决手段,对于近场声全息技术的进一步推广具有重要的实际意义.
5.结论
本文在前期对声场分离技术研究的基础上,基于欧拉公式和有限差分近似,以全息面上声压和质点振速同时作为输入量,推导出了新的基于声压-速度测量的平面近场声全息理论公式.该方法通过建立和求解两侧声源在全息面上的声压和质点振速耦合关系,可以实现全息面来自两侧声波的分离,从而解决了常规的近场声全息要求所有声源均位于全息面的同一侧,即测量声场为自由声场的限制.对两音箱声源的实验研究验证了基于声压-速度测量的平面近场声全息的有效性,结果表明:利用该公式可以有效分离出全息面两侧声源各自在全息面上辐射的声压;采用分离后的声压可以有效重建出目标声源各声学参量,能够有效排除全息面另一侧干扰声源带来的影响.该方法的采用为近场声全息技术在实际工业环境下的应用提供了新的解决手段,对于近场声全息技术的进一步推广具有重要的实际意义
[1]W illiams E G,Maynard J D 1980Phys.Rev.Lett.45 554
[2]Maynard J D,W illiams E G,Lee Y 1985J.Acoust.Soc.Am. 78 1395
[3]BaiM R 1992J.Acoust.Soc.Am.92 533
[4]Kim B K,Ih J G 1996J.Acoust.Soc.Am.100 3003
[5]Wang Z,Wu S F 1997J.Acoust.Soc.Am.102 2020
[6]Wu S F 2004J.Acoust.Soc.Am.115 207
[7]Steiner R,Hald J 2001Int.J.Acoust.Vib.6 83
[8]Bi C X,Chen X Z,Chen J,Zhou R 2005Sci.Chin.Ser.E 48 338
[9]Sarkissian A 2004J.Acoust.Soc.Am.115 1593
[10]Yu F,Chen J,Chen X Z 2003Acta Acustica28 385(in Chinese)[于 飞、陈 剑、陈心昭2003声学学报28 385]
[11]Yu F,Chen J,LiW B,Chen X Z 2005Acta Phys.Sin.54 789 (in Chinese)[于 飞、陈 剑、李卫兵、陈心昭2005物理学报54 789]
[12]TamuraM 1990J.Acoust.Soc.Am.88 2259
[13]Yu F,Chen X Z,Chen J 2004Chin.J.Mech.Eng.40 112(in Chinese)[于 飞、陈心昭、陈 剑2004机械工程学报40 112]
[14]LiW B,Yu F,Chen J,Bi C X,Chen X Z 2005Acta Phys. Sin.54 1253(in Chinese)[李卫兵、于 飞、陈 剑、毕传兴、陈心昭2005物理学报54 1253]
[15]Hald J 2006Proceedings of EuronoiseTampere,Finland,May 30-June 1,2006
[16]Jacobsen F,Jaud V 2007J.Acoust.Soc.Am.121 1550
[17]Jacobsen F,Chen X Y,Jaud V 2008J.Acoust.Soc.Am. 123 1842
[18]Langrenne C,Melon M,Garcia A 2007J.Acoust.Soc.Am. 121 2750
[19]Valdivia N P,W illiams E G,Herdic P C 2008J.Acoust.Soc. Am.123 109
[20]Bi C X,Chen C X,Chen J 2008J.Acoust.Soc.Am.123 1472
PACC:4320,4363
An exper imental investigat ion of planar nearfield acoustic holography using pressure and particle velocity measurements*
Bi Chuan-Xing†Zhang Yong-Bin Xu Liang Chen Xin-Zhao
(Institute of Sound and Vibration Research,Hefei University of Technology,Hefei 230009,China)
6 May 2009;revised manuscript
31 May 2009)
In the conventional nearfield acoustic holography(NAH),only the pressure or particle velocity is used as the input quantity,and it cannot separate the waves from the two sides of the hologram surface.Therefore,all sources are assumed to be on one side of the hologram surface,i.e.the sound field is assumed to be free.This assumption limits the practical applications of NAH.In the NAH using pressure and particle velocity measurements,both pressure and particle velocity are used as the input quantities.By establishing and solving the coupling relationship on the hologram surface between the waves from the two sides of the hologram surface,the waves from the two sides can be separated.On the basis of the previous studies on sound field separation techniques and based on the Euler formula and the finite difference approximation technique,a new theoretical formula of NAH using pressure and particle velocity measurements is given, and then an experiment is performed to validate the method.
nearfield acoustic holography,sound field separation,sound field reconstruction,sound source identification
*国家自然科学基金(批准号:10874037,10974040)、霍英东教育基金(批准号:111058)和教育部新世纪优秀人才支持计划(批准号: NCET-08-0767)资助的课题.
†E-mail:cxbi@hfut.edu.cn
*Project supported by the National Natural Science Foundation of China(Grant Nos.10874037,10974040),the Fok Ying Tung Education Foundation,China(GrantNo.111058),and the Program for New Century Excellent Talents in University of Ministry of Education of China (GrantNo.NCET-08-0767).
†E-mail:cxbi@hfut.edu.cn

