偏振干涉成像光谱仪中格兰-泰勒棱镜全视场角透过率的分析与计算*
张淳民 刘 宁 吴福全
1)(西安交通大学理学院,非平衡物质结构与量子调控教育部重点实验室,西安 710049)
2)(曲阜师范大学激光研究所,曲阜 273165)
偏振干涉成像光谱仪中格兰-泰勒棱镜全视场角透过率的分析与计算*
张淳民1)†刘 宁1)吴福全2)
1)(西安交通大学理学院,非平衡物质结构与量子调控教育部重点实验室,西安 710049)
2)(曲阜师范大学激光研究所,曲阜 273165)
(2009年1月18日收到;2009年6月19日收到修改稿)
论述了自行设计研制的偏振干涉成像光谱仪的工作原理,分析了其核心部件格兰-泰勒棱镜的分光机理;运用光线追迹方法,推导出了格兰-泰勒棱镜全视场角透过率计算公式;通过计算机模拟分析了入射面、入射角和空气隙厚度对该棱镜透过率的影响,并利用方解石Sellmeier色散方程,给出了该棱镜在仪器系统要求的光谱范围内透过率与波长的关系曲线;实验测试结果与理论计算公式相符,验证了理论公式的正确性.
偏振干涉成像光谱仪,格兰-泰勒棱镜,透过率,多光束干涉
PACC:4225B,4280G,0765
1.引言
1996年,美国华盛顿大学研制了基于Wollaston棱镜角剪切的数字阵列扫描干涉成像光谱仪(DASI),它是一种静态的空间调制型干涉成像光谱仪,其缺点是含有由空间分辨率决定的狭缝,从而对远距离目标和微弱信号的探测受到限制.2000年以来,张淳民、相里斌、赵葆常等[1—20]提出了时空混合的新型偏振干涉成像光谱技术,并研制了基于Savart偏光镜的稳态偏振干涉成像光谱仪(SPIIS)和稳态大视场偏振干涉成像光谱仪(SLPIIS).由于以视场光阑取代了入射狭缝,从而具有超小型、高稳态、高通量、大视场和高分辨率等显著特点.
格兰-泰勒棱镜是该偏振干涉成像光谱仪中的重要偏光器件,它采用冰洲石晶体设计而成,由于冰洲石晶体的光学性能好、光谱透射范围广、双折射率大,且棱镜采用空气隙胶合,所以它的消光比优于10-5,使用光谱范围为300—2500 nm[21],是获得偏振光不可缺少的重要偏光器件.曲阜师范大学激光研究所对格兰-泰勒棱镜的理论和制造工艺有较为深入的研究,但对于其透过率的分析大都局限于主截面内[22].文献[23]运用空间几何的方法讨论了全视场角下棱镜的透过率,但并没有给出全视场角下棱镜透过率精确的计算公式.本文采用光线追迹的方法推导了全视场角下(任意入射面、任意入射角)棱镜的透过率精确计算公式,运用Matlab软件进行了详细的分析,并将主截面内实验测得数据与理论计算所得的数据进行了对比,验证了理论计算公式的正确性.该研究对偏振干涉成像光谱仪的研制具有指导意义.
2.偏振干涉成像光谱仪原理与偏光镜格兰-泰勒棱镜分光机理
图1是偏振干涉成像光谱仪的原理图,它的核心部分是偏振干涉仪,其主要由Savart偏光镜、起偏器P1和检偏器P2组成,其主要作用是进行横向剪切.从光源s发出的一束光,经P1后变为沿P1偏振化方向振动的一束线偏振光,经Savart偏光镜后被剪切成两束振动面相互垂直的线偏振光,通过检偏器变成振动方向完全一致的二束线偏振光,经成像镜后在探测器上相遇,形成干涉图样.对干涉图采集并经傅氏变换,即可得到光源的光谱分布,经系统处理,即可得到光源的像.

图1 偏振干涉成像光谱仪的原理图
偏振干涉成像光谱仪中使用格兰-泰勒棱镜作为起偏器和检偏器.其结构如图2所示,它由两块直角形方解石组成,两切割面间隔有等厚的空气隙,两块方解石晶体的光轴如箭头所示,都平行于入射端面和出射端面,S是棱镜的结构角.一束自然光经过端面1入射到格兰-泰勒棱镜后,由于e光和o光的折射率不同,在晶体切割面2处o光发生全反射,e光保持原来的入射方向,从端面4射出.最终出射格兰-泰勒棱镜的光为偏振方向平行于纸面的线偏振光.由于格兰-泰勒棱镜的起偏方向在纸平面方向,故作为起偏器和检偏器用于偏振干涉成像光谱仪中,将两个格兰-泰勒棱镜沿光学系统光轴同时旋转45°放置,如图3所示.
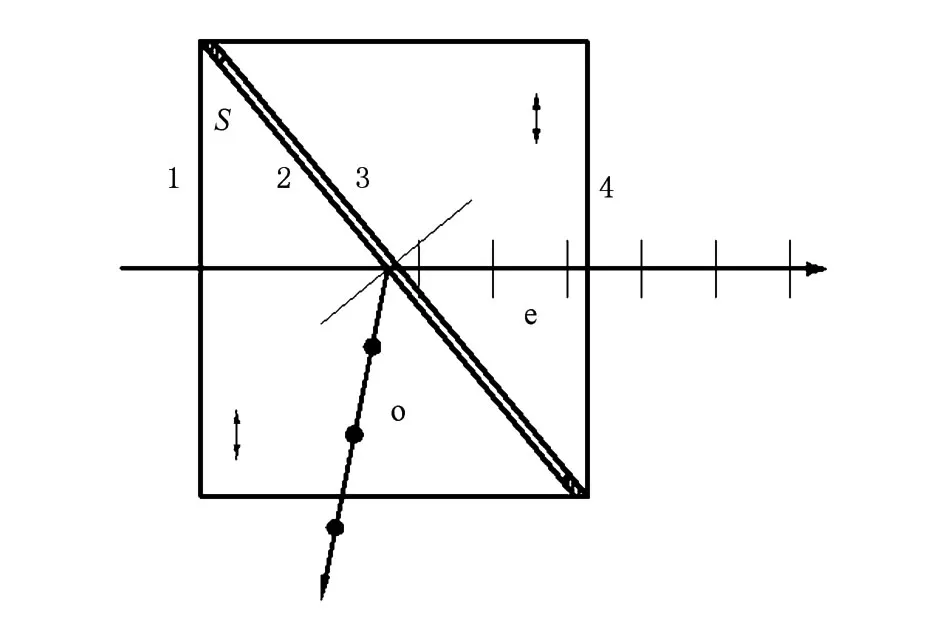
图2 格兰-泰勒棱镜结构示意图

图3 格兰-泰勒棱镜在偏振干涉成像光谱仪中应用示意图
3.格兰-泰勒棱镜全视场角透过率的分析与计算
3.1.格兰-泰勒棱镜中的光路计算
光线入射到格兰-泰勒棱镜只有e光透过,因此只讨论e光在棱镜中的传播规律.如图4所示,以入射端面1的中心为坐标原点建立坐标系,z轴为晶体的光轴方向,x轴为棱镜界面的法线方向.光线从空气中以任意入射角i入射棱镜中,波矢k的折射角为θe且与晶体光轴的夹角为θ.xoz面为主截面,入射面和棱镜主截面之间的夹角为ω.由几何关系可以得到e光波矢为[24]

并且

其中n′e为e光波矢的折射率
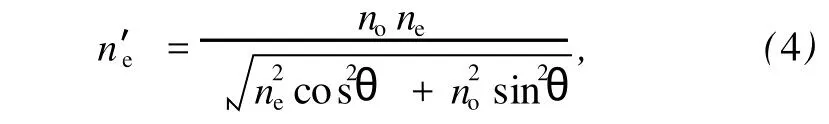
这里no,ne为晶体的主折射率.
联立(2)—(4)式可得


图4 e光在格兰-泰勒棱镜中传播示意图
在单轴晶体中光线s往往与波矢方向存在一定的离散角,设光线与光轴之间的夹角为ξ,则

已知棱镜的光轴方向为w=(0,0,1),它与e光波矢、光线方向满足关系式
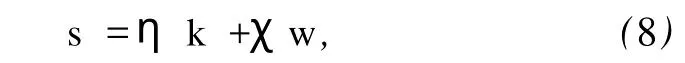
又有s·w=cosξ,s =1,k·w=coθs,因此光线方向为

其中
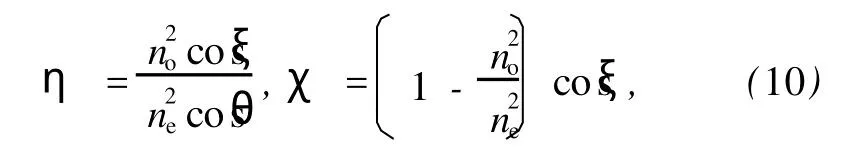
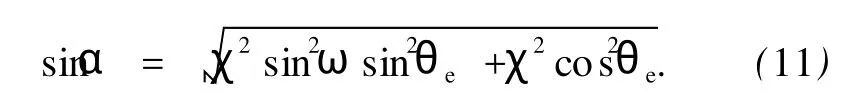
通过(1),(6)和(9)式可得出e光波矢和光线入射端面1到切割面2的传播方向.下面讨论e光波矢从切割面2到切割面3的传播过程.设波矢在界面2上的入射角为i′,在空气隙中的折射角为θ′.由几何关系可知n为界面2的法线方向,n=(cosS,0,sinS),所以
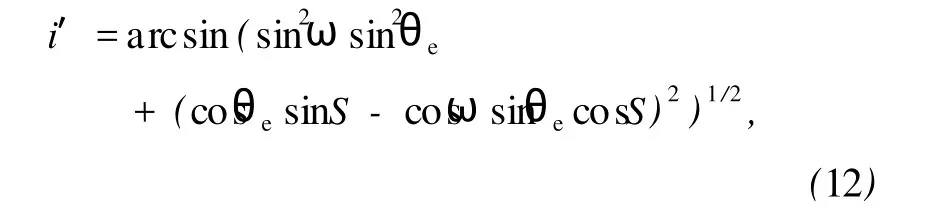
波矢在入射面内满足折射定律

代入(5)和(12)式可得波矢(光线)在空气隙内的传播方向,即

由于空气隙等厚的特性,e光在第二块晶体中的传播方向和在第一块晶体中的情况一致,故不另加讨论.
综上所述,通过(1),(6),(9),(12)和(14)式可以精确地确定任意入射面入射角e光波矢和光线在格兰-泰勒棱镜中的传播规律.
3.2.全视场角透过率公式的推导
由上可知,e光波矢和光线往往不在同一个平面内,二者存在一定的离散角,故格兰-泰勒棱镜在端面1和端面4的透射系数一般需要运用电磁场理论来进行求解,其过程相当繁琐[25].但在格兰-泰勒棱镜的实际应用中,其视场角一般不会超过3.5°,e光波矢和光线之间的离散角α是非常小的.例如,在ω=45°的入射面内以3.5°入射,由(6)和(11)式可得出离散角α仅为0.3°.所以,在这样的小角度入射且棱镜厚度很小的情况下(约为25 mm),可以近似认为e光的波矢和光线的方向一致.因此,可以运用菲涅耳公式来计算端面1和端面4的反射系数

若不考虑界面对光的吸收,则e光在端面1和端面4的透过率为


e光在空气隙处的传播情况比较复杂,将在空气隙两表面上发生振荡反射,产生多光束干涉,如图5所示.
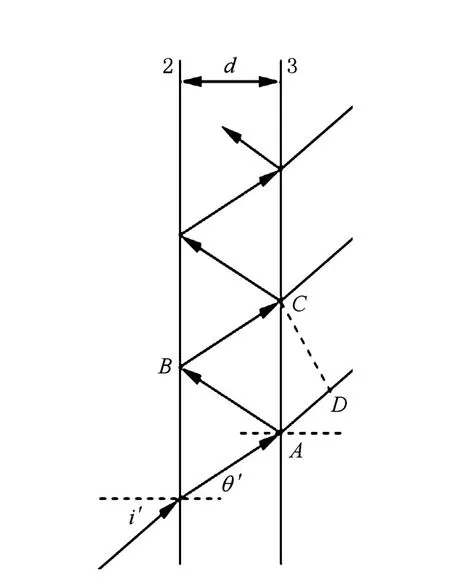
图5 空气隙之间的多光束干涉
根据多光束干涉理论可知e光在空气隙处的透过率为[25]
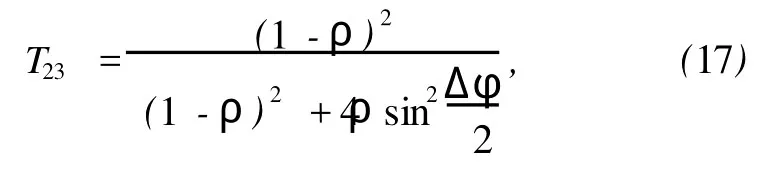
式中Δφ为光波在两界面内传播引起的相邻相干光束的位相差,由几何关系和折射定律可得
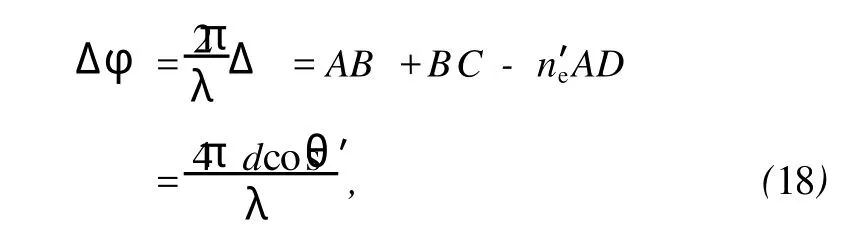
ρ为空气隙内表面的反射率,由下式给出:

联立(16)和(17)式可得到棱镜任意入射面和入射角e光的透过率Te,

其中,n′e,θe,i′,θ′和ρ分别由(5),(6),(12),(14)和(19)式可得.
考虑以下两种特殊情况:
1)光线在主截面内入射的情况,即ω=0°.由(5),(6),(12)和(14)式可得
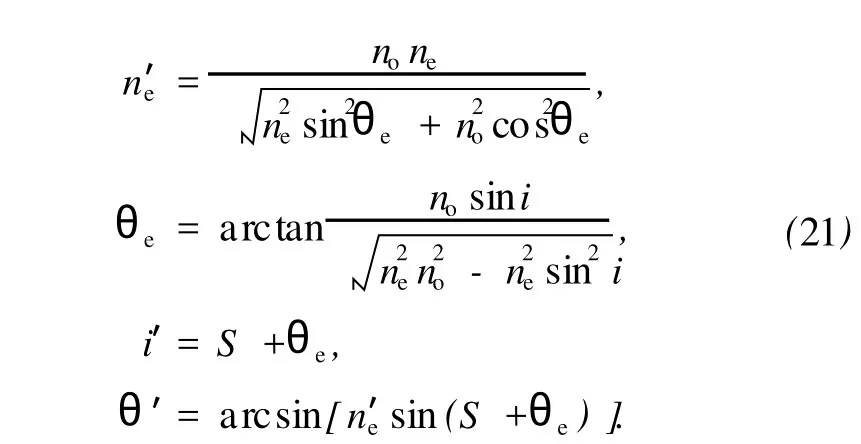
代入(20)式可得主截面内棱镜的透过率表达式.
2)光线正入射时的情况,即i=0°,ω=0°.由(5),(6),(12),(14)和(20)式可得正入射棱镜的透过率

4.格兰-泰勒棱镜全视场角透过率的计算机模拟

图6 格兰-泰勒棱镜透过率随入射角度和空气隙厚度变化的三维图 (a)ω=0°,(b)ω=30°,(c)ω=60°,(d)ω=90°
由(20)式可知,格兰-泰勒棱镜的透过率是关于ω,i,d,S和λ的函数.在进行计算机数值计算之前,应该对这些量进行约定.如图2所示,考虑到棱镜的对称性,只需分析ω在0°—90°的范围.对于入射角度的符号规定如下:下光线(以xoy面为基准从上到下的入射光线)取正值,上光线(以xoy面为基准从下到上的入射光线)为负值.按照系统的要求,格兰-泰勒棱镜的最大入射角为3.5°,结构角S= 39.6°.设定λ=632.8 nm,d的变化范围设为1000—36000 nm.运用Matlab软件,根据(20)式得到透过率Te随入射角度i和空气隙厚度d变化的三维图(见图6),四个分图分别是入射面和棱镜主截面之间的夹角ω为0°,30°,60°和90°时的情况.以下将对其进行详细分析.
4.1.入射面对棱镜透过率的影响
比较图6的四幅分图可看出,不同入射面内格兰-泰勒棱镜的透过率之间的差别非常大.图7对其中三个入射面的透过率随入射角变化曲线进行了比较,从曲线振荡的幅值和周期可以看出,ω越大透过率振荡的周期越大,而其振荡幅值越小.并通过计算可知,ω=0°,60°和90°的三个入射面的透过率平均值分别为78.17%,81.94%和82.87%.因此,主截面(ω=0°)内透过率随入射角的振荡最为剧烈且其透过率最低,而在垂直主截面(ω= 90°)内的透过率随入射角的振荡最为平稳且其透过率最高,其他入射情况介于二者之间.所以,主截面内光线透过率过低成为限制器件整体的透过率的主要瓶颈,这也是常常在主截面内讨论格兰-泰勒棱镜透过率的原因所在.

图7 不同入射面的透过率随入射角变化曲线的比较
4.2.入射角对棱镜透过率的影响
图8是主截面内(ω=0°),厚度d=30000 nm时整个孔径角范围空气隙透过随入射角的变化曲线.可以看出,棱镜透过率是一个随入射角增大呈急剧振荡衰减趋势的函数.不同入射角对应的透过率有很大的差异,透过率在某些角度能达到峰值的92.5%,而边缘光线(入射角i=3.5°)e光透过率仅为19.6%.

图8 主截面内透过率与入射角的关系曲线
4.3.空气隙厚度对棱镜透过率的影响
图9是在正入射(i=0°)时,透过率随空气隙厚度的变化曲线.可以看出,透过率随空气隙的厚度按余弦函数变化.计算可得,透过率随空气隙厚度在峰值的92.28%与谷值的74.5%之间余弦振荡.可见空气隙厚度对透过率的影响非常大,恰当选择空气隙的厚度,可以使得棱镜的透过率达到最大值.因此,选用适当厚度的垫层来保证一定的空气隙厚度,可实现对棱镜的优化设计.

图9 正入射时透过率与空气隙厚度的关系曲线
4.4.入射波长对棱镜透过率的影响
仪器系统要求的光谱范围为480—960 nm,如此宽的光谱范围,方解石的色散必须考虑.方解石Sellmeier色散方程(λ/μm)为[26]

运用(22)—(24)式,可以得出正入射时格兰-泰勒棱镜透过率与波长的关系曲线.图10为d= 30μm时透过率随波长的变化曲线.由图10可看出,随着波长的增大透过率呈现出上升趋势,并具有明显的波动特征.经计算,在480—960 nm的光谱范围内正入射时棱镜的透过率介于72.84%—92.54%之间,其平均值能达到83.04%.

图10 正入射时透过率与波长的关系曲线
5.格兰-泰勒棱镜透过率实验测试
为了验证理论结果的正确性,我们对格兰-泰勒棱镜在不同入射角下的透过率进行了测试.图11展示了该实验测试系统几个主要组成部分.
用计算机控制步进电机带动起偏器转动,直到输出光强最大停止转动,用探测器测出此时经过起偏器后的光强值I0.转动测角仪的样品台,使入射光束位于主截面内并以入射角i入射到待测棱镜上,记录下此时的输出光强I,则该棱镜在入射角i下的透过率Te=I/I0.通过旋转测角仪可以得到不同入射角下棱镜的透过率,从而得到入射角和棱镜透过率的关系曲线.

图11 实验系统示意图 1为半导体激光器,2为衰减器,3为标准起偏器,4为测角仪的样品台,5为待测棱镜,6为探测器, 7为光功率计,8为计算机,9为A/D转换器,10为电机[27].标准起偏器在步进电机的控制下旋转,电机运转由计算机控制
待测格兰-泰勒棱镜样品的结构角S=39.6°,空气隙厚度d=0.03 mm.测试数据如图12所示,其中“*”点表示不同入射角下的透过率测试数据.并由(20)和(21)式,可得到透过率随入射角变化的理论曲线(如图12中实线所示).对比可知,实验数据与理论值二者十分接近,经计算,其平均相对误差为7.3%;从理论曲线上可看出主截面内棱镜的透过率随入射角度增大呈急剧振荡衰减趋势,而实验值也正好显示了这一趋势,由此验证了理论计算公式的正确性.

图12 不同入射角下透过率实验和理论数据的对比
6.讨论
下面对实验产生误差的原因及透过率曲线呈现出的急剧振荡衰减趋势的原因进行讨论.
1)产生误差的两个主要原因:一是在理论分析中,忽略了晶体材料对光的吸收作用,并近似认为e光的波矢和光线方向一致,造成理论数值和实验数值存在一定的偏差.对于上述这一近似造成的偏差需做以下补充说明:通过电磁场理论,可严格推导出主截面内棱镜端面1和端面4的反射系数[28]

其中,α为e光波矢和光线之间的离散角,由(11)式给出.由于入射角i≤3.5°,计算可得α非常小.在一级近似条件下,cosα≈1,即α≈0(e光的波矢和光线方向一致),此时(25)式可用(15)式代替.这一近似引入的理论数值与实验数据之间的偏差分布如图13所示,可见其偏差值始终保持在10-3量级上.因此这一近似引入的误差很小,说明此近似方法具有很好的可靠性.
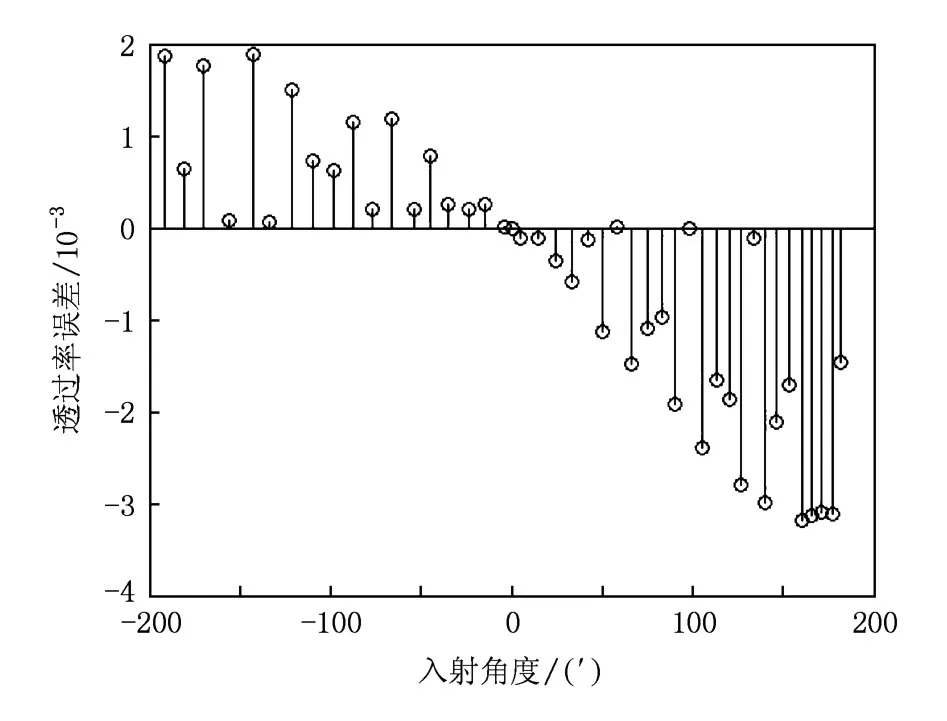
图13 近似方法引入的理论值与实验数据之间的偏差
产生误差的另一个原因是由于主截面内光的透过率随入射角的变化非常敏感,在实验中样品台微小的角度误差就会严重影响测得的结果.这方面是产生误差的主要原因,在实验测试中应予以重视.
2)小角度入射时,格兰-泰勒棱镜入射和出射端面反射系数基本保持不变,所以空气隙处的透过率的变化趋势决定整个棱镜的透过率的变化趋势.计算可得光线经空气隙时其入射角i′变化范围为16.56°—41.98°,在这个范围内晶体切割面的透过系数随入射角的增加急剧降低,从而导致棱镜整体透过率随入射角增大急剧衰减;同时由于空气隙处的多光束干涉,入射角度的不同导致光透过空气隙后可能干涉加强或干涉相消,故棱镜的透过率随入射角度的变化会出现振荡特征.
7.结论
1)运用光线追迹方法,结合菲涅耳公式和多光束干涉理论,给出的格兰-泰勒棱镜全视场角(任意入射面和入射角时)透过率的理论计算公式,与目前国内外文献报道的公式相比更加精确和具有普遍性.
2)通过对格兰-泰勒棱镜的透过率进行的实验测试,其结果与理论计算公式相符,验证了理论公式的正确性.
3)采用计算机模拟给出的入射面、入射角和空气隙厚度与棱镜透过率的关系曲线表明:与其他的入射面相比,主截面内棱镜的透过率随入射角变化振荡最为剧烈,且其透过率值最小,成为限制器件整体的透过率的主要瓶颈;棱镜透过率是一个随入射角增大而急剧衰减的振荡函数;棱镜透过率随空气隙的厚度按余弦函数变化,在实际应用中适当选取空气隙的厚度可实现对格兰-泰勒棱镜的优化设计.
4)从正入射时格兰-泰勒棱镜在仪器系统要求的光谱范围内透过率与波长的关系看出,随着入射波长的增大,格兰-泰勒棱镜透过率呈现出上升趋势,并具有明显的波动特征.同时计算得出在480—960 nm的光谱范围内,格兰-泰勒棱镜的平均透过率可达到83.04%,对干涉成像光谱仪的研制提供了理论依据和实践指导.
[1]Zhang CM,Yan X G,ZhaoB C 2008Opt.Commun.281 2050
[2]Zhang C M,He J 2006Opt.Express14 12561
[3]Zhang CM,XiangliB,Zhao B C 2004J.Opt.A:Pure Appl. Opt.6 815
[4]Zhang C M,Zhao B C,XiangliB 2004Appl.Opt.43 6090
[5]Zhang C M,XiangliB,Zhao B C 2002Opt.Commun.203 21
[6]Zhang C M,Zhao B C,XiangliB,Li Y C 2006Optik117 265 [7]Zhang C M,Zhao B,XiangliB 2003Opt.Commun.227 221
[8]Zhang C M,XiangliB,Zhao B C 2000Proc.SPIE4087 957
[9]Zhang C M,Zhao B C,Yuan Y,He J 2006Proc.SPIE 6032 60320T1
[10]Zhang CM,ZhaoB C,Yuan ZL,HuangW J 2009J.Opt.A: Pure Appl.Opt.11 085401
[11]Zhang C M,Sun M Z,Yuan Z L,Song X P 2009Acta Phys. Sin.58 1758(in China)[张淳民、孙明昭、袁志林、宋晓平2009物理学报58 1758]
[12]Ren W Y,Zhang C M,Mu T K 2009Chin.Phys.Lett. 26 084209
[13]Zhang CM,Zhao B C,XiangliB 2000Acta Opt.Sin.20 1077(in Chinese)[张淳民、赵葆常、相里斌2000光学学报20 1077]
[14]Zhang C M,Xiangli B,Yang J F,Zhao B C 2000J.Xi’an Jiaotong Univ.34 93(in Chinese)[张淳民、相里斌、杨建峰、赵葆常2000西安交通大学学报34 93]
[15]Peng Z H,Zhang C M,Zhao B C,Li Y C,Wu F Q 2006Acta Phys.Sin.55 6374(in Chinese)[彭志红、张淳民、赵葆常、李英才、吴福全2006物理学报55 6374]
[16]Wu L,Zhang C M,Zhao B C 2007Opt.Commun.273 67
[17]Yuan Z L,Zhang C M,Zhao B C 2007Acta Phys.Sin.56 6413(in Chinese)[袁志林、张淳民、赵葆常2007物理学报56 6413]
[18]Jian X H,Zhang C M,Zhao B C 2007Acta Phys.Sin.56 824 (in Chinese)[简小华、张淳民、赵葆常2007物理学报56 824]
[19]Ye J Y,Zhang CM,Zhao B C 2007Acta Phys.Sin.57 67(in Chinese)[叶健勇、张淳民、赵葆常2007物理学报57 67]
[20]He J,Zhang C M,Zhang Q G 2007Spectroscopy and Spectral Analysis27 423(in Chinese)[贺 健、张淳民、张庆国2007光谱学与光谱分析27 423]
[21]Liao TB 2003Polarization Optics(Beijing:Science Press)p62 (in Chinese)[廖延彪2003偏振光学(北京:科学出版社)第62页]
[22]Shi M,Wu F Q,Fan J Y 2005 Optics&Optoelectronic Technology 3 50(in Chinese)[史 萌、吴福全、范吉阳2005光学与光电技术3 50]
[23]Zhu H F,SongL K,Zhen C H,Wang XM 2004Acta Photon. Sin.33 204(in Chinese)[朱化凤、宋连科、郑春红、王秀民2004光子学报33 204]
[24]Wu H Y,Zhang CM,Zhao B C 2008Acta Phys.Sin.57 3499 (in Chinese)[吴海英、张淳民、赵葆常2008物理学报57 3499]
[25]BornM,WolfW(Jranslated by Yang J S)1985Principles of Optics(Ⅰ)(Beijing:Science Press)p61(in Chinese)[波恩M、沃尔夫E著(杨葭荪译)1985光学原理(上册)(北京:科学出版社)第61页]
[26]Zhao T S,Li G H,Peng H D,Jia P 2007Chinese J.Lasers34 1383(in Chinese)[赵廷生、李国华、彭捍东、贾 朋2007中国激光34 1383]
[27]Kong F Z(M.S.Thesis)2006(Qufu:Qufu NormalUniversity) p35(in Chinese)[孔凡震2006(曲阜:硕士学士论文)第35页]
[28]Song Z,Liu L R,Zhou Y,Liu D A 2004Acta Opt.Sin.24 1701(in Chiness)[宋 哲、刘立人、周 煜、刘德安2004光学学报24 1701]
PACC:4225B,4280G,0765
Analysis and calculat ion of Glan-Taylor prism’s transm ittance at full angle of view in a polarization interference im aging spectrometer*
Zhang Chun-Min1)†Liu Ning1)Wu Fu-Quan2)
1)(Key Laboratory forNon-equilibrium Condensed M atter and Quantum Engineering of M inistry of Education,School of Science, Xi’an Jiaotong University,Xi’an 710049,China)
2)(Laser Research Institute,Qufu No rmal University,Qufu 273165,China)
18 January 2009;revised manuscript
19 June 2009)
The principle of the polarization interference imaging spectrometer(PIIS)developed in our laboratory is described. The principle of the beam splitting of Glan-Taylor prism which is one of the key components in the PIIS is analyzed.Using the ray-tracingmethod,we obtain the transmittance of Glan-Taylorprism at full angle of view.By computer simulation,we analyze the influence of the incidence plane,incidence angle and thickness of air gap on transmittance,and the dependence of the transmittance on wavelength is given in the spectral range which is required by the instrument system using Sellmeier dispersion equation.The transmittance of Grand-Taylor prism is tested in experiment,and the results are in good agreement with the theoretical results,so the correctness of the theory is verified.
polarization interference imaging spectrometer,Glan-Taylor prism,transmittance,multiple-beam interference
*国家自然科学基金重点项目(批准号:40537031)、国家高技术研究发展计划(批准号:2006AA12Z152)、国防基础科学研究基金(批准号:A1420080187)、国家自然科学基金(批准号:40875013,40375010,60278019)、陕西省科技攻关计划(批准号:2001K06-G12,2005K04-G18)和西安交通大学“985”二期电子信息平台资助的课题.
†E-mail:zcm@mail.xjtu.edu.cn
*Project supported by the Key Program of theNationalNatural Science Foundation of China(GrantNo.40537031),the NationalHigh Technology Research and Development Program of China(GrantNo.2006AA12Z152),the NationalDefense Basic Scientific Research Foundation of China (GrantNo.A1420080187),the NationalNatural Science Foundation of China(GrantNos.40875013,40375010,60278019),the Science and Technology Key Program of Shaanxi Province,China(GrantNos.2001K06-G12,2005K04-G18),and the Second Phase of the“985 Project”of the Electronic Information Platform of Xi’an JiaotongUniversity,China.
†E-mail:zcm@mail.xjtu.edu.cn

