狭义相对论下电子自旋轨道耦合对X射线光谱的影响*
余志强 谢 泉 肖清泉
(贵州大学理学院,新型光电子材料与技术研究所,贵阳 550025)
狭义相对论下电子自旋轨道耦合对X射线光谱的影响*
余志强 谢 泉†肖清泉
(贵州大学理学院,新型光电子材料与技术研究所,贵阳 550025)
(2009年4月26日收到;2009年4月29日收到修改稿)
基于狭义相对论的基本观点,研究了特征X射线的产生机理,分析了电子自旋轨道耦合对特征X射线波长的影响,导出了一个计算特征X射线波长的公式,同时对计算推导的波长值做了系统的误差分析,得到了相对误差的规律.结果表明,计算推导的波长值与实验的波长值非常接近,在实际应用中对分析特征X射线光谱具有一定的参考意义.
狭义相对论,特征X射线,自旋轨道耦合,误差分析
PACC:3220R
1.引言
X射线是1895年被伦琴发现的,是一种波长很短的电磁波,波长范围为0.001—10 nm,具有非常强的穿透力.1912年德国物理学家劳厄发现X射线通过晶体时产生衍射现象,证明了X射线的波动性.X射线光谱已被广泛地应用于晶体的结构分析和材料的元素分析等领域,对于促进科学技术的发展产生了巨大而深远的影响.
在分析特征X射线光谱时,通常取的电子质量都是原子核外电子的静质量,一般都没有考虑在狭义相对论下电子自旋轨道耦合对特征X射线光谱的影响.
本文基于爱因斯坦狭义相对论[1]的基本理论原理,在经典量子理论的基础上,研究了特征X射线[2]的辐射机理,分析了在狭义相对论下电子自旋轨道耦合对特征X射线波长的影响,得到了一个计算特征X射线波长的公式,并且对常见元素的特征波长做了理论的推导计算,通过计算所得到的波长值与实验的波长值非常接近,在实际应用中对分析特征X射线光谱具有一定的参考意义.
2.X射线光谱分析的基本原理
X射线光谱通常由连续谱和特征谱组成.对于X射线光谱,其连续谱是由高能电子与构成阳极靶的原子碰撞时,电子失去动能所辐射出的光子产生的.由于每个电子可能产生多次碰撞,而每次碰撞电子所损失的能量又可能不同,因此辐射出的不同频率的光子形成了连续X射线谱.
而在X射线光谱中,其特征X射线表征的是各元素的本征特性,特征X射线与阳极靶的组成元素紧密相关,它和可见光谱一样,是由原子内部电子做能级跃迁辐射[3]光子的结果.但是由于X射线光子能量比可见光光子的能量大得多,所以不可能是原子中外层电子的能级跃迁的结果,但可以用内壳层电子的能级跃迁来加以解释.然而在正常情况下,由于原子的内壳层都已填满了电子,根据泡利不相容原理[4]可知,电子不可能再跃入.在这里高能加速电子的碰撞起了关键的作用,高能加速电子的碰撞可以将内壳层的电子击出原子,而在原来位置留下一个空穴.根据能量最低原理,处在较高能级的不稳定电子会跃入低能级空穴而形成稳定状态,而在电子的跃迁过程中就会辐射出具有一定频率的高能量的X射线.由于离原子核越远之处电子所产生的跃迁概率越小,所以高次辐射的强度也就越来越弱,因此在特征X射线光谱分析中,通常主要采用的是Kα辐射,它近似一束单色的特征X射线.
考虑到电子自旋轨道耦合[5]对电子运动状态的影响,电子的自旋轨道耦合使原来简并的能级分裂开来,当n和l(l>0)都确定后,j可以取两个值即具有相同的量子数n和l的能级有两个,它们之间的差别很小.通常把电子由L层的2p1/2态和2p3/2态跃迁填充K层1s1/2态空穴时所形成的特征X射线称为Kα辐射,同理还有Kβ辐射、Kγ辐射.
如果将电子由L层的2p1/2态和2p3/2态跃迁填充K层1s1/2态空穴所产生的特征波长分别表示为λ1/2和λ3/2,由于λ1/2和λ3/2的值很接近,并且在特征Kα辐射中λ3/2出现的概率是λ1/2的两倍,于是特征X射线的Kα辐射波长公式可表示为如下形式:

根据爱因斯坦光子能量公式[6]E=2πħf,只要能够知道特征X射线的波长就可以间接地确定靶的组成元素,实现对靶的测定和分析.以及通过已知的X射线的Kα辐射波长λ和晶体掠射角θ,就可以对晶体的晶面间距d进行测定,从而分析晶体的周期特性[7].
3.狭义相对论下的电子自旋轨道耦合
狭义相对论涉及的是无加速运动的惯性系,它是根据爱因斯坦的相对性原理的假设和光速不变原理的假设而创立起来的一套完整的理论.
根据狭义相对论的基本观点,在洛伦兹变换[8]的基础上,可以得到在相对论中运动电子的质量与速率的关系

其中μ为电子的相对论质量,μ0为电子的静质量,v为电子的速率,c为光速.
由于核外电子的速率主要由轨道速率所决定,于是核外电子的相对论质量μn可以由Bohr-Sommerfeld量子化条件和库仑电势表示为如下的形式:

式中,σn,l,j为屏蔽常数(n为主量子数,l为轨道量子数,j为总动量量子数),z为原子序数,es为SI制电子电量.从(3)式可以知道,电子的相对论质量μn是与主量子数n相关的函数.
在相对论电子自旋轨道耦合中,电子自旋对原子能级和谱线都有影响,电子的总角动量由其自旋角动量和轨道角动量共同耦合形成,电子自旋角动量和轨道角动量之间相互作用的能量与电子的动能以及电子在核的力场中的势能相比很小,它可以被看做是微扰能量.
4.狭义相对论下电子自旋轨道耦合对X射线光谱的影响分析
特征X射线表征的是各元素的本征特性,它是各原子的内层电子跃迁辐射的结果.通过原子内部较外层的电子跃迁填充就会辐射出能量光子,本文基于爱因斯坦狭义相对论的基本原理,在经典量子理论的基础上,研究特征X射线的辐射机理,分析在狭义相对论中电子自旋轨道耦合微扰对特征X射线的Kα辐射波长的影响.
考虑狭义相对论下电子自旋微扰的影响(即考虑电子自旋轨道耦合的影响),在电子库仑屏蔽的作用下,对原子序数为z的原子,其K层电子填满时具有两个电子,考虑同层电子间的库仑屏蔽作用,其屏蔽常数[9]σ1,0,1/2约为1,对其中一个电子,另一个电子近似受到核电荷数为z-1的库仑场作用.当K层出现空穴,L层电子向K层跃迁填充时,L层内2p1/2态的电子受到K层电子的库仑屏蔽作用,其屏蔽常数σ2,1,1/2约为1,其L层内2p3/2态屏蔽常数σ2,1,3/2约为1,于是L层2p态的电子近似受到核电荷数为z-1的库仑场作用.
当不考虑电子自旋角动量和轨道角动量相互作用的耦合能量时,核外电子体系的哈密顿算符可表示为

考虑核外电子的屏蔽,则电子库仑电势为

其中r为电子到核的距离.
Bohr-Sommerfeld量子化条件为

其中,p为广义动量,q为广义坐标.
将(5)式代入(6)式,可得

考虑电子自旋角动量和轨道角动量相互作用的耦合能量.根据经典量子理论,原子核外电子是分层排布的,电子的总角动量由其自旋角动量和轨道角动量共同耦合形成,电子的总角动量[10]算符可表示为


于是,在考虑电子自旋角动量和轨道角动量相互作用时,核外电子体系的含′微扰项的哈密顿算符可表示为
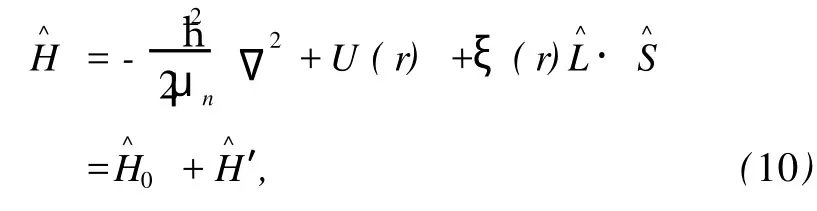
其中,



其中m为磁量子数.
根据简并条件下的微扰理论

其中

由于J^2=(L^+S^)2=L^2+S^2+2L^·S^,S^2=

将(18)式代入(17)式,有

如果令

将(5)式代入(20)式可得

于是

将(22)式代入(16)式,可得

在微扰条件下的一级修正能量可表示为

将(21)式代入(24)式,有

由此可见,自旋轨道耦合使原来简并的能级分裂开来,当n和l(l>0)都确定后,j可以取两个值即具有相同的量子数n和l的能级有两个;而当n=1和l=0时,j只有一个值即 1s1/2态的电子没有自旋轨道耦合,因而能级没有移动.
考虑狭义相对论质量μn的影响,于是量子数为态的电子能量分别为

将(3)和(7)式分别代入(26)—(28)式,可以得到在狭义相对论中,2p3/2态,2p3/2态和1s1/2态的电子能量.
2p3/2态的电子能量为


2p1/2态的电子能量为
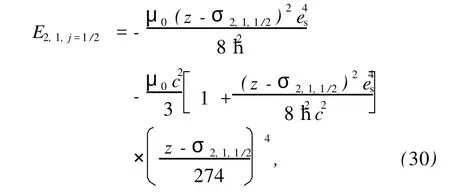
1s1/2态的电子能量为

其中,ħ=1.05×10-34J·s,μ0=9.11×10-31kg,es= 1.52×10-14C,c=3.00×108m/s,σ1,0,1/2=σ2,1,1/2=σ2,1,3/2.
电子由L层跃迁填充K层所形成的特征X射线的Kα辐射过程如图1所示.
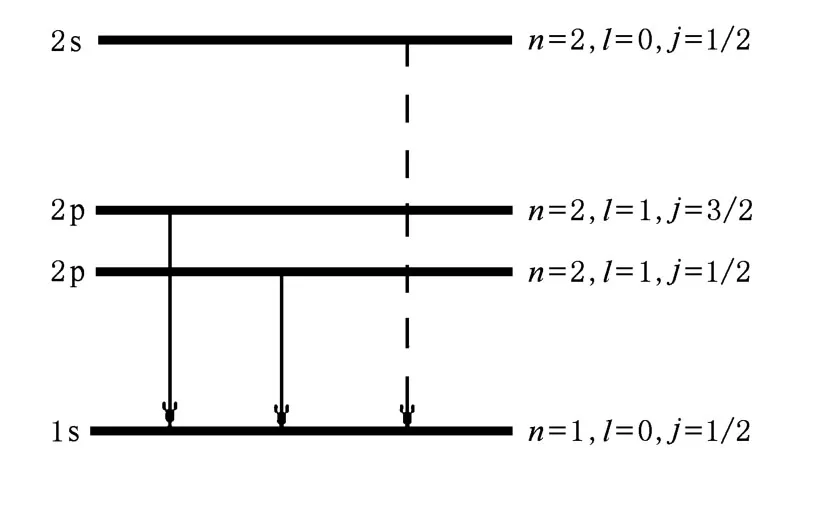
图1 形成特征X射线的Kα辐射过程简图
电子由L层的2p1/2态和2p3/2态跃迁填充K层1s1/2态空穴所形成的X射线波长λ1/2和λ3/2分别表示为

将(32)式代入(1)式,得到计算特征X射线的Kα辐射波长公式

5.结果及分析
根据(33)式特征X 射线波长的计算公式,可以理论计算出Mg,Ca,Fe等元素的Kα辐射波长,将计算的各波长分别与文献[11]的实验波长相比较,如表1所示.

表1 特征X射线的Kα辐射波长的计算值与实验值比较
分析表1中的数据,可以看出,理论计算推导的各元素Kα辐射波长值与它们各自所对应的实验波长值非常接近,并且随着原子序数的增加,两者间的相对误差成规律性的变化.在原子序数11—40的范围内,相对误差大致在0.5%左右;在原子序数41—60的范围内,相对误差大致在2.5%左右;在原子序数61—76的范围内,相对误差大致在6%左右;在原子序数77—90的范围内,相对误差大致在9%左右.

图2 特征X射线的Kα辐射波长的计算值与实验值比较
通过图2所示的特征X射线的Kα辐射波长的计算值与实验值比较及变化规律可以知道,Kα辐射波长的计算值与实验值两者之间非常接近,并且随着原子序数的增加,它们之间的Kα辐射波长的变化规律基本上一致.
通过(33)式所推导的计算特征X射线波长的计算公式,可以对物质元素进行测定以及对晶体的周期性结构进行理论研究.利用布拉格方程[12]2dsinθ=nλ,如果知道晶体的晶面间距d,掠射角θ,就可以计算特征X射线的波长λ,通过(33)式就可以确定组成靶的各种元素.通过已知的晶体掠射角θ和特征X射线的Kα辐射波长λ,利用布拉格方程就可以计算出晶体的晶面间距d,从而分析晶体的周期性结构.
6.结 论
基于狭义相对论的基本原理,在经典量子理论的基础上,研究了特征X射线的辐射机理,分析了在狭义相对论下电子自旋轨道耦合对特征X射线波长的影响,得到了一个计算特征X射线波长的公式,并且其计算推导的各元素Kα辐射波长值与实验的波长值相比也是非常接近的,这在实际应用中对分析特征X射线光谱具有一定的参考意义.
[1]Einstein A 1905Annalen der Physik17 891
[2]Quarles C,SemaanM 1982Phys.Rev.A 26 3147
[3]Li J,Dong C Z,Xie L Y 2006Acta Phys.Sin.55 655(in Chinese)[李 杰、董晨钟、颉录有2006物理学报55 655]
[4]PauliW 1925Z Physik31 765
[5]Gouds mit SA,Uhlenbeck G E 1925Natur wissenchaften13 953
[6]Einstein A 1905Annalen der Physik17 132
[7]Yu ZQ,Xie Q,Xiao Q Q,Zhao K J 2009Acta Phys.Sin.58 6889(in Chinese)[余志强、谢 泉、肖清泉、赵珂杰2009物理学报58 6889]
[8]Lorentz H A 1904Proc.Roy.Soc.Amst.6 809
[9]PaisA 1986Inward Bound of Matter and Forces in the Physical World(New York:Oxford University Press)p229
[10]ThomasL H 1926Nature117 514
[11]Bearden J A 1967Rev.M od.Phys.39 78
[12]BraggW L 1913Proc.Cam.Phil.Soc.17 43
PACC:3220R
Effects of the spin-orbit coupling on X-ray spectrum in special relativity*
Yu Zhi-Qiang Xie Quan†Xiao Qing-Quan
(Institute of Advanced OptoelectronicM aterials and Technology,College of Science,Guizhou University, Guiyang 550025,China)
26 April 2009;revised manuscript
29 April 2009)
Based on special relativity,the formation mechanism of characteristic X-ray was studied,and the influence of the spin-orbit coupling on the characteristic X-ray wavelength was analyzed.A calculation formula of the X-ray wavelength based on special relativity is obtained.Error analysis is carried out systematically for the calculation values ofwavelength, and the rules of relative error are obtained.It is shown that the results of the calculation are very close to the experimental results,which have some reference meaning for spectrum analysis of characteristic X-ray in application.
special relativity,characteristic X-ray,spin-orbit coupling,error analysis
*国家自然科学基金(批准号:60566001,60766002)、科技部国际合作专项基金(批准号:2008DFA52210)、贵州省信息产业厅基金(批准号:0831)和贵阳市科学技术计划(批准号:[2008]15-3)资助的课题.
†通讯联系人.E-mail:qxie@gzu.edu.cn
*Project supported by theNationalNatural Science Foundation ofChina(GrantNos.60566001,60766002)the Special Foundation for International Cooperation of the Ministry of Science and Technology of China(Grnat No.2008DFA52210),the Foundation of the Infor mation Industry of Guizhou Province,China(GrantNo.0831),and the Science-Technology Program of Guiyang,China(GrantNo.[2008]15-3).
†Corresponding author.E-mail:qxie@gzu.edu.cn

