LS解法和Fisher方程行波系统的定性分析*
李向正 张卫国 原三领
1)(上海理工大学理学院,上海 200093)
2)(河南科技大学理学院,洛阳 471003)
LS解法和Fisher方程行波系统的定性分析*
李向正1)2)†张卫国1)原三领1)
1)(上海理工大学理学院,上海 200093)
2)(河南科技大学理学院,洛阳 471003)
(2009年4月16日收到;2009年6月26日收到修改稿)
提出了求解非线性发展方程的新方法——LS解法.LS解法是基于(G’/G)展开法和扩展的双曲正切函数展开法.并引入了Poincaré定性理论的思想,然后以Fisher方程为例进行了试验.通过定性分析首先获得了Fisher方程行波系统积分曲线的性质,然后解得了Fisher方程作为耗散系统时单调减少的波前解和作为扩张系统时单调递增的波前解.一些试验结果与Ablowitz所得结果一致.也得到了Fisher方程作为扩张系统时的新结果.LS解法是在定性理论指导下,在已获知解曲线性质的情况下进行精确求解的,求解目标明确.LS解法揭示了线性系统也可以用作辅助方程来求解非线性系统.
Fisher方程,行波解,定性分析,LS解法
PACC:0340K,0420J,0547
1.引言
非线性发展方程(NEE)的精确解(如行波解)具有重要的物理意义和数学意义,它涉及了数学中几乎所有主流分支,吸引了一大批当代前沿物理学家和数学家对其进行研究[1—18].使用现代数学的理论及方法解决重要的物理问题是理论物理前沿研究的主流[19—23].由于NEE个性突出,求解NEE是困难而具有挑战性的工作,目前没有统一的求解方法.近年来,多种获取NEE精确解的方法被陆续提出,如反散射方法[18]、Hirota方法[24]、Lamb’sAnsatz方法[25]、齐次平衡方法[1,2,26]、Jacobi椭圆函数展开方法[5]、双曲正切函数展开法[27]及其扩展方法[26]、F展开法[28—31]、线性化解法[32]、(G′/G)-展开法[33—36]等.值得指出的是,扩展的双曲正切函数展开法、F展开法和线性化解法属于辅助常微分方程方法[16,37,38](简称sub-ODE方法[37]),其要点在于能够将一个复杂的非线性偏微分方程的行波解表示成简单、可解的常微分方程(ODE)解的多项式,这个ODE称为sub-ODE.函数展开方法和辅助方程方法均将NEE的求解问题转化为非线性代数方程组的求解问题.非线性代数方程组(或称多元多项式方程组)的求解是非线性科学中最基本的问题之一.吴文俊消元法为非线性代数方程组的求解建立了完整的理论,提供了有效的算法[39,40].
求解NEE的方法都有它的适用范围.Pavel等[41]指出反散射方法、Hirota方法和Lamb’s Ansatz方法对于带有耗散项的系统不适用.刘式适等[5]指出,齐次平衡方法、双曲正切函数展开法及其扩展方法等无法获得非线性波动方程的周期解,为此提出的Jacobi椭圆函数展开方法解决了求周期解的问题.一种方法对某类问题失效的时候,正是该方法发展或新方法产生的契机.
19世纪初Abel和Galois已经证明了5次及5次以上的多项式一般不能用根式求解.1841年,在Abel的思想基础上,Liouville证明了一般Riccati方程不能用积分法求解[42,43].这从理论上结束了人们对一般常微分方程求通解的努力,一方面促使人们研究常微分方程的可积性,使此后常微分方程的可积性理论得到了较系统的发展;另一方面,它更促使人们去寻找新的途径和新方法,从给定微分方程本身可提供的信息来研究其解的性质.Poincaré开创的常微分方程定性理论就是在分析与几何工具的帮助下,从微分方程本身提供的信息出发,几何地反映出解曲线的性质[44—48].常微分方程定性理论中的非线性动力系统和分支理论对物理问题的研究起到了重要作用[49—53].中国在定性理论的研究方面居于世界前列[44,54—57].
NEE经行波约化后转化为非线性常微分方程(NODE),因而求NEE的行波解实际上是求解NODE.在利用定性理论分析精确行波解的动力学行为,判断精确行波解如何依赖于系统的参数条件,并选择合适的方法求出重要的行波解方面, Pavel等[41]、李继彬等[11]、张卫国等[58]和冯兆生[59]已做了一些开拓性的工作.Pavel等[41]利用定性理论分析了平方Fisher方程的静态解,给出了一些近似解.李继彬等[11]用相平面方法深入研究了一个非线性色散可积偏微分方程的孤波解和周期波解及其存在的条件,并给出了部分精确解.张卫国等[58]利用Lienard方程给出了几个判定非线性演化方程孤波解的公式,借助该判别方法和解公式求解了几个著名的非线性演化方程.冯兆生[59]利用常微分方程定性理论分析了近似Sine-Gordon方程,并利用首次积分法进行了求解.
研究数学物理方程的中心内容是求各类定解问题的解并研究解的性质,使我们对其所描述的自然现象或过程有更深入的认识[6].数学物理方程的解法的选取随定解问题的不同而有所调整.既然Poincaré定性理论能够根据微分方程提供的信息判断积分曲线的性质,我们可以根据获得的积分曲线的性质选择解法或构造新的解法,并构造解的Ansatz形式.对固定奇点附近解的性态的研究,将有助于掌握方程解的全局性质.通过方程的固定奇点的解通常与其临近的其他解具有不同的解析性质和拓扑性质,有其特殊意义[60].在不动点附近,线性项是主项,经常决定非线性方程在不动点附近的性态[61],如线性系统常用来确定不动点的稳定性.
受上述思路启发,我们将对NEE的行波解进行定性分析,并提出NEE的LS解法.所谓LS解法就是经过对非线性系统作Poincaré定性分析后,根据获得的积分曲线的性质,选择对应的平面线性自治系统,再利用该平面线性自治系统向径的斜率,根据齐次平衡原则来构造NEE的行波解.LS解法的关键在于一是选择线性平面自治系统做辅助,二是利用平面线性自治系统向径的斜率来构造解.因而我们抽取“线性”和“斜率”这两个关键词来命名LS解法.
下面以平方Fisher方程为例来进行定性分析并展示LS解法的思想.
2.Fisher方程背景简介及研究进展
反应扩散方程涉及的大量问题来自物理学、化学和生物学中众多的数学模型,具有丰富的实际背景,其中著名的反应扩散方程之一是Fisher方程[62—67]

这类方程建立了人口中有利基因的传播以及调节单双分子化学反应扩散的动力学模型,其中D,a,b是非负系数.Fisher方程被广泛应用于人口增长模型、热传导、神经生理学、自身催化的化学反应、布朗运动过程和核反应理论.Fisher方程还可用来描述流体力学、等离子体物理和传染病传播等问题中的非线性现象[64].更多有关Fisher方程的信息参见文献[41,65,66].
本文考虑正规化Fisher方程[67,68]

在化学媒介中函数u(x,t)指反应物浓度,因而u(x, t)≥0.作为描述人口中有利基因传播的动力学模型[62],Fisher于1937年提出Fisher方程.直到1979年,Ablowitz和Zeppetella[67]首先注意到Fisher方程(1)具有Painleve性质,然后他们利用Laurent展开获得了方程(1)的一个精确行波解.文献[63]将有限差分方法和配置法相结合给出了Fisher方程的数值解.文献[64]用待定系数法得到了Fisher方程的新的行波解及行波波速.文献[41,65—67]均只考虑了Fisher方程波速c>0的耗散系统,而没有考虑c<0的扩张系统[68].
3.Fisher方程行波约化和对应的行波系统
我们要寻找Fisher方程(1)的行波解

其中常数c为波速.将(2)式代入方程(1)得q满足的常微分方程

方程(3)为Lienard方程.令y1=q,˙y1=y2,则方程(3)等价于系统
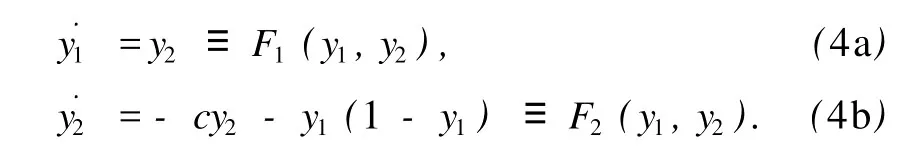
设V=(˙y1,˙y2),则散度当c=0时,divV=0,Fisher方程(1)为保守系统;当c>0时,divV<0,Fisher方程(1)为耗散系统;当c< 0时,divV>0,Fisher方程(1)为扩张系统.当物质反应产生后向外扩散时,反应物浓度将单调递增,因而研究Fisher方程(1)作为扩张系统时单调递增的波前解也具有重要的意义.
4.系统(4)的奇点及其类型判定
系统(4)有两个有限奇点(0,0),(1,0).根据常系数线性系统奇点的参数判定法和Perron定理[44],(1,0)点不论c取何值始终为鞍点;当c>2时,(0,0)点是稳定结点;当c=2时,(0,0)点是稳定退化结点;当0 根据中心-焦点判定中的对称原理[44],当c=0时,(0,0)点是中心. 考虑到Fisher方程(1)的物理意义,要求浓度q≥0,因而(0,0)点不能为焦点.波速c=0时Fisher方程表示静态解的变化,因而我们也不考虑(0,0)点为中心的情况. 无穷远奇点及特殊分界线有助于我们分析系统有限区域的动力学行为.系统(4)经Poincaré变换(y1,y2)=(1/z,u/z)后不存在(u*,0)型的奇点,而经变换(y1,y2)=(v/z,1/z)后所得系统中D(0, 0)点为Lyapunov型奇点中的结点.z=0为Poincaré变换后所得系统的解. 显然,系统(4)的奇点对应平衡解(y1,y2)= (0,0)和(y1,y2)=(1,0),而y1=0(y2轴)和y2=0 (y1轴)不是解. 从前面的定性分析可知,系统(4)当参数c≤-2时存在连结(0,0)点和(1,0)点的y2>0的有界轨线,当参数c≥2时存在连结(1,0)点和(0,0)点的y2<0的有界轨线.我们用LS解法来试验求解这两类有界轨线. 根据齐次平衡原则[1,2,26,28—36],设系统(4)有如下形式的解: 其中k=z2/z1,z1,z2满足平面线性自治系统 (5),(6)式中μ>0为待定常数,线性系统(6)的解易于求出,其奇点(0,0)为鞍点类型,系统(6)中轨线向径的斜率k为 其中A1,A2为任意常数. 将(5)式代入系统(4)中,利用(6)式可知(4a)式自动成立,(4b)式变成关于k的多项式方程,令k的各幂次项的系数等于0,得到关于a0,a1,a2,c和μ的代数方程组(n代表k的幂次) 解上述方程组得四组解 将(8a)—(8d)四组解分别代入(5)式,结合(7)式可得到系统(4)的精确行波解 其中 若取A =0,即得 其中 若取A2=0则得 (y1,y2)6对应的解2与文献[67]中的结果一致. 当c=56/6时,系统(4)作为耗散系统存在有界精确解(0,0),(1,0)和(y1,y2)6,其中(y1,y2)6为从奇点(1,0)运动到奇点(0,0)的有界轨线. 当c=-5 6/6时,系统(4)作为扩张系统存在有界精确解(0,0),(1,0)和(y1,y2)4,其中(y1,y2)4为从奇点(0,0)运动到奇点(1,0)的有界轨线. 本文提出了新的求解平面自治系统的LS解法,并将其融入Fisher方程行波解的定性分析之中,研究了Fisher方程行波解的丰富的动力学行为.LS解法利用线性平面自治系统向径的斜率来构造非线性平面自治系统的解,这是此方法的新颖之处.在定性理论中,线性自治系统可以用于判断奇点的类型,还可以用于确定不动点的稳定性.LS解法进一步揭示了一些线性自治系统也可以用作辅助方程来求解非线性自治系统.而线性平面自治系统的动力学性质及解的情况已是众所周知的知识.LS解法中用于辅助的线性平面自治系统如何选取,要依赖于对非线性平面自治系统的定性分析,这方面的工作今后值得进一步研究.LS解法所得到的精确解仍是有限的,因而对Fisher方程的求解需引入更多的求解方法. 感谢王明亮教授和张金良教授对本文工作提出了建设性意见. [1]WangM L 1995Phys.Lett.A 199 169 [2]Li ZB 2002Acta Math.Sci.B 22 138 [3]ZhangW G,MaW X 1999Appl.M ath.M ech.20 666 [4]Qu C Z,Zhang SL,Liu R C 2000PhysicaD 144 97 [5]Liu S K,Fu Z T,Liu SD,Zhao Q 2001Phys.Lett.A 289 69 [6]Gu C H,LiD Q,Chen S X,Zheng SM,Tan Y J 2002Equation of M athematical Physics(Beijing:Higher Education Press)(in Chinese)[谷超豪、李大潜、陈恕行、郑宋穆、谭永基2002数学物理方程(北京:高等教育出版社)] [7]Geng X G,Cao C W 1999Phys.Lett.A 261 289 [8]Xin H W 1999Nonlinear Chem istry(Hefei:China University of Science and Technology Press)(in Chinese)[辛厚文1999非线性化学(合肥:中国科学技术大学出版社)] [9]Guo B L 1995Nonlinear Evolution Equation(Shanghai:Shanghai Science and Technology Education Press)(in Chinese)[郭柏灵1995非线性演化方程(上海:上海科技教育出版社)] [10]Li Y S,Zhang J E 2003Chaos Soliton.Fract.16 271 [11]Li J B,Liu Z R 2000Appl.M ath.M odell.25 41 [12]Feng Z S 2003Chaos Soliton.Fract.17 861 [13]Lou S Y,Ma H C 2006Chaos Soliton.Fract.30 804 [14]Shang YD 2005Chaos Soliton.Fract.25 1083 [15]Zhang J F,Wu FM 2000Commun.Nonl.Sci.Numer.Simul.5 170 [16]Li X Z,WangM L 2007Phys.Lett.A 361 115 [17]Li X Z,Li X Y,Zhao L Y,Zhang J L 2008Acta Phys.Sin.57 2031(in Chinese)[李向正、李修勇、赵丽英、张金良2008物理学报57 2031] =0,则得 [18]AblowitzM J,Clarkson P A 1991Solitons,Nonlinear Evolution EquationsandInverseScatteringTransfor m(Cambridge: Cambridge University Press) [19]LinW T,Mo J Q 2008Acta Phys.Sin.57 6689(in Chinese) [林万涛、莫嘉琪2008物理学报57 6689] [20]LuW T,Wang S J,Zhang H 2007Acta Phys.Sin.56 3655(in Chinese)[卢伟涛、王顺金、张 华2007物理学报56 3655] [21]Ding P Z,Liu X S,Luo X Y 2007Acta Phys.Sin.56 604(in Chinese)[丁培柱、刘学深、罗香怡2007物理学报56 604] [22]Deng Z C,HuW P 2008Chin.Phys.B 17 3923 [23]Fu J L,Weng YQ,Xu S S 2008Chin.Phys.B 17 1939 [24]Hirota R A 1974Prog.Theor.Phys.52 1498 [25]Leibbrandt G 1976Phys.Rev.B 15 3353 [26]Fan E G,Zhang H Q 1998Phys.Lett.A 246 403 [27]Lan H B,Wang KL 1990J.Phys.A 23 4097 [28]Zhou YB,WangM L,Wang YM 2003Phys.Lett.A 308 31 [29]WangM L,Zhou YB 2003Phys.Lett.A 318 84 [30]Li X Z,Li X Y,WangM L 2005M ath.Appl.18 303 [31]Li X Z,Zhang J L,Wang YM,WangM L 2004Acta Phys.Sin. 53 4045(in Chinese)[李向正、张金良、王跃明、王明亮2004物理学报53 4045] [32]Li X Z,Zhang X Y,Zhao L Y 2007J.Henan Univ.Sci.Techn. 28 70(in Chinese)[李向正、张小勇、赵丽英2007河南科技大学学报28 70] [33]WangM L,Li X Z,Zhang J L 2008Phys.Lett.A 372 417 [34]WangM L,ZhangJ L,LiX Z 2008Appl.Math.Comp.206 321 [35]Zhang S,Tong J L,WangW 2008Phys.Lett.A 372 2254 [36]AhmetB 2008Phys.Lett.A 372 3400 [37]Sirendaoreji,Sun J 2003Phys.Lett.A 309 387 [38]Yomba E 2005Phys.Lett.A 336 463 [39]Li Z B 2007W ave Solutions of NonlinearMathematical Physics Equation(Beijing:Science Press)p158(in Chinese)[李志斌2007非线性数学物理方程的行波解(北京:科学出版社)第158页] [40]Wu W J 2003Mathematics M echanization(Beijing:Science Press)p357(in Chinese)[吴文俊2003数学机械化(北京:科学出版社)第357页] [41]Pavel KB,John J T 1999SIAM J.Appl.M ath.60 371 [42]Feng Z S,Fei SM 1997J.SoutheastUniv.27 69(in Chinese) [冯兆生、费树岷1997东南大学学报27 69] [43]Waston GN 1952A Treatise on theBessel Functions(Cambridge: Cambridge University Press)p110 [44]Qian X Z,DaiB X,Liu K Y2006Theory,M ethod and Application of Nonlinear Ordinary Differential Equations(Changsha:Hunan University Press)p1(in Chinese)[钱祥征、戴斌祥、刘开宇2006非线性常微分方程理论、方法、应用(长沙:湖南大学出版社)第1页] [45]PoincaréH 1881J.M ath.Pures et Appl.7 375 [46]PoincaréH 1882J.M ath.Pures et Appl.8 251 [47]PoincaréH 1885J.M ath.Pures et Appl.1 167 [48]PoincaréH 1886J.M ath.Pures et Appl.2 151 [49]Jin Y F,Xu W,Zou S C 2008Acta Phys.Sin.57 7527(in Chinese)[靳艳飞、徐 伟、邹少存2008物理学报57 7527] [50]He X J,WangW,ZhangQ C 2008Acta Phys.Sin.57 5384(in Chinese)[何学军、王 炜、张琪昌2008物理学报57 5384] [51]Wang ZL 2008Acta Phys.Sin.57 4771(in Chinese)[王作雷2008物理学报57 4771] [52]Liu F H,WangW,ZhangQ C 2008Chin.Phys.B 17 4123 [53]Chen Z Q,WuW J,Yuan Z Z 2008Chin.Phys.B 17 2420 [54]Zhang J Y1987Geometric Theory and B ranch Poblem of Ordinary Differential Equations(Beijing:Beijing University Press)(in Chinese)[张锦炎1987常微分方程几何理论与分支问题(北京:北京大学出版社)] [55]Zhang Z F,Ding T R,Huang W Z,Dong Z X 1985Qualitative Theory of Differential Equations(Beijing:Science Press)(in Chinese)[张芷芬、丁同仁、黄文灶、董镇喜1985微分方程定性理论(北京:科学出版社)] [56]Han M A,Zhu D M 1994B ifurcation Theory of Differential Equations(Beijing:Coal Industry Press)(in Chinese)[韩茂安、朱德明1994微分方程分支理论(北京:煤炭工业出版社)] [57]Ma Z E,Zhou Y C 2001Qualitative and Stability Methods of Ordinary Differential Equations(Beijing:Science Press)(in Chinese)[马知恩、周义仓2001常微分方程定性与稳定性方法(北京:科学出版社)] [58]ZhangW G,Chang Q S,Fan E G 2003J.M ath.Anal.Appl. 287 1 [59]Feng Z S 2002Phys.Lett.A 302 64 [60]Lei J Z,Guan K Y 2001Chin.Ann.M ath.22A 571(in Chinese)[雷锦志、管克英2001数学年刊22A 571] [61]Robinson R C(Translated by Han M A,Xing Y P,Bi P)2007 AnIntroductionto Dynam ical Systems(Beijing:Machinery Industry Press)p96(in Chinese)[Robinson R C著(韩茂安、邢业朋、毕 平译)2007动力系统导论(北京:机械工业出版社)第96页] [62]Fisher R A 1937Ann.Eugen.7 353 [63]Bi H,Lu T C 2004J.Shandong Univ.(Science Edition)39 41 (in Chinese)[闭 海、鲁统超2004山东大学学报(理学版) 39 41] [64]Tao T,Zhang W G,Feng L P 2004J.Univ.Shanghai Sci. Techn.26 111(in Chinese)[陶 涛、张卫国、冯丽萍2004上海理工大学学报26 111] [65]Tan Y,Xu H,Liao S J 2007Chaos Soliton.Fract.31 462 [66]Feng Z S,Li Y 2006PhysicaA 366 115 [67]AblowitzM J,Zeppetella A 1979Bull.M ath.B iol.41 835 [68]Wang G X,Zhou Z M,Zhu S M,Wang S S 2006Ordinary Differential Equation(Beijing:Higher Education Press)p316 (in Chinese)[王高雄、周之铭、朱思铭、王寿松2006常微分方程(北京:高等教育出版社)第316页] PACC:0340K,0420J,0547 LS method and qualitative analysis of traveling wave solut ions of Fisher equation* Li Xiang-Zheng1)2)†ZhangWei-Guo1)Yuan San-Ling1) 1)(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China) 16 April 2009;revised manuscript 26 June 2009) LS method,a new method for solving nonlinear evolution equations,is proposed.It is based on the(G′/G)–expansion method and the extended hyperbolic tangent function method,and the Poincaré’s qualitative theory is also led in.Then Fisher equation is tested as an example.The properties of integral curves for traveling wave system of Fisher equation are obtained through qualitative analysis,and then a monotonically decreasing wave-front solution of Fisher equation as a dissipative system and a monotonically increasing wave-front solution of Fisher equation as an expansion system are obtained too.Some results agree with that ofAblowitz et al.and some new results for Fisher equation are also obtained as an expansion system.The LS method is used to look for the exact solutions under the condition that the property of solution curves have been obtained through the qualitative analysis,and the target is clear.The LSmethod also reveals that a linear system can also be used as auxiliary equations to solve nonlinear systems. Fisher equation,traveling wave solution,qualitative analysis,LS method *国家自然科学基金(批准号:10871129)、上海市重点学科建设计划(批准号:S30501)和上海市研究生创新基金(批准号: JWCXSL090114)资助的课题. †E-mail:lylxz@mail.haust.edu.cn *Project supported by the National Natural Science Foundation of China(Grant No.10871129),the Shanghai Leading Academic Discipline Program,China(GrantNo.S30501),and the Innovation Fund for Graduate Student of Shanghai,China(GrantNo.JWCXSL090114). †E-mail:lylxz@mail.haust.edu.cn5.系统(4)的特殊积分曲线及LS解法
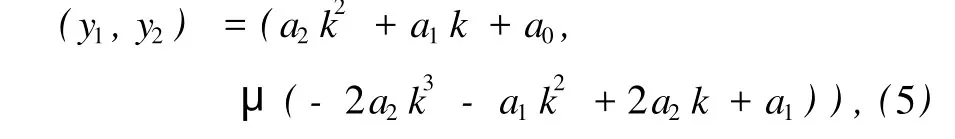







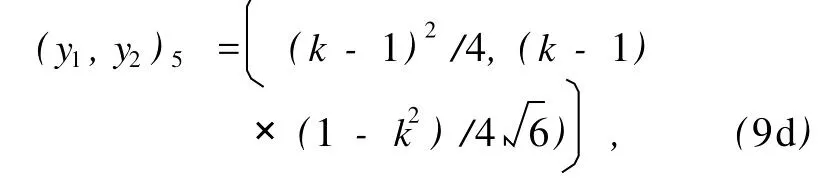
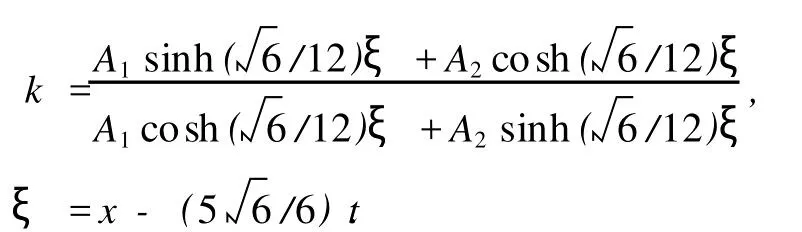

6.结论
2)(College of Science,Henan University of Science and Technology,Luoyang 471003,China)

