颗粒堆的体积分数与制备流量关系的实验研究＊

孔维姝 胡 林 张兴刚 岳国联

(贵州大学理学院,贵州光电子技术与应用重点实验室,贵阳 550025)

颗粒堆的体积分数与制备流量关系的实验研究＊

孔维姝†胡 林 张兴刚 岳国联

(贵州大学理学院,贵州光电子技术与应用重点实验室,贵阳 550025)

(2009年2月20日收到;2009年5月7日收到修改稿)

通过实验研究发现,颗粒堆的体积分数随制备颗粒堆的颗粒流流量指数衰减,减小或增加流量到一定程度时,体积分数都达到饱和;出料口直径与颗粒粒径的比值小到一临界值时,随着流量的减小体积分数增加急剧变缓;颗粒粒径小到一临界值时,随着流量的增加,体积分数的减小急剧变缓.结合颗粒物质的强耗散性、空气作用、瓶颈效应和碰撞理论解释了实验现象,从连续性原理出发推出的颗粒堆体积分数随制备流量变化的函数与实验数据的拟合公式相同.

颗粒物质,流量,体积分数

PACC:4630P,4610,8220M

1.引言

颗粒物质一般指由尺度d>1μm的大量离散固体颗粒组成的复杂体系,它有许多不同于固体、液体、气体的奇特性质,颗粒物质的独特性质之一是颗粒物质的行为与它形成历史有关,表面上看起来完全相同的颗粒堆其内部结构可以有很大差别,导致它的行为也相差甚远.颗粒物质的这一性质引起人们广泛的关注[1—8],其中具有代表性的是1999年以来Vanel等精心设计的一些实验,文献[1]证明了颗粒堆的制备方式不同引起的颗粒堆底部压力凹陷的不同,文献[2]证明了颗粒堆的制备方式不同引起的粮仓效应的差异,无论是压力凹陷还是粮仓效应,都与颗粒堆的结构有关,颗粒物质的体积分数(颗粒堆中每颗颗粒的体积之和与颗粒堆所占的空间体积的比值)是描述颗粒物质结构和影响颗粒物质性质的重要物理量,颗粒物质的行为不仅静态的甚至动态的都与它的体积分数有关,例如,任何颗粒流动的发生都是以局部颗粒堆积密度的降低(体积分数减小)为条件的.对于固体和流体,当温度和压力确定时,其密度是确定的.颗粒堆中的颗粒无序分布,其密度(或体积分数)则不确定,与堆积方式和历史有关.大量的实验证明,对尺寸相近的颗粒用不同方式制备的颗粒堆,其体积分数约在0.56—0.64的范围内,若颗粒的大小不同,堆积的体积分数会更大.理论上可以证明,相同尺寸球形颗粒物质的无序堆积的体积分数低于有序面心(或六方)密堆积时的体积分数0.74,而高于简单立方堆积的体积分数0.52.二维颗粒堆积的体积分数比三维堆积的体积分数高[3].在我们的调研中,未见到关于颗粒堆体积分数与制备颗粒堆的颗粒流流量关系的报道,我们提出一种新的重复性较好的制备颗粒堆的方式,通过改变制备颗粒堆的流量来改变它的体积分数,可控体积分数在0.589—0.640范围内.结合颗粒物质的强耗散性、空气作用、瓶颈效应和碰撞等理论解释了实验现象,并从连续性原理出发推出了颗粒堆的体积分数随制备流量变化的函数,此函数与实验数据的拟合函数完全相同.

2.实验

实验中,颗粒堆由大量的球形玻璃珠构成,10种玻璃珠的密度都为ρ0=2.50 g/cm3,直径在0.04 cm到0.40 cm范围内;粒径不同的10堆颗粒的总质量M相同,其值为M=600 g;容器的内径和高度分别为3.15 cm和56.00 cm(在预实验中,我们分别用直径为7.00 cm和3.15 cm的容器制备颗粒堆,得到的颗粒堆的体积分数相同,为了提高测量精度,我们使用了较细而深的圆筒容器制备颗粒堆).

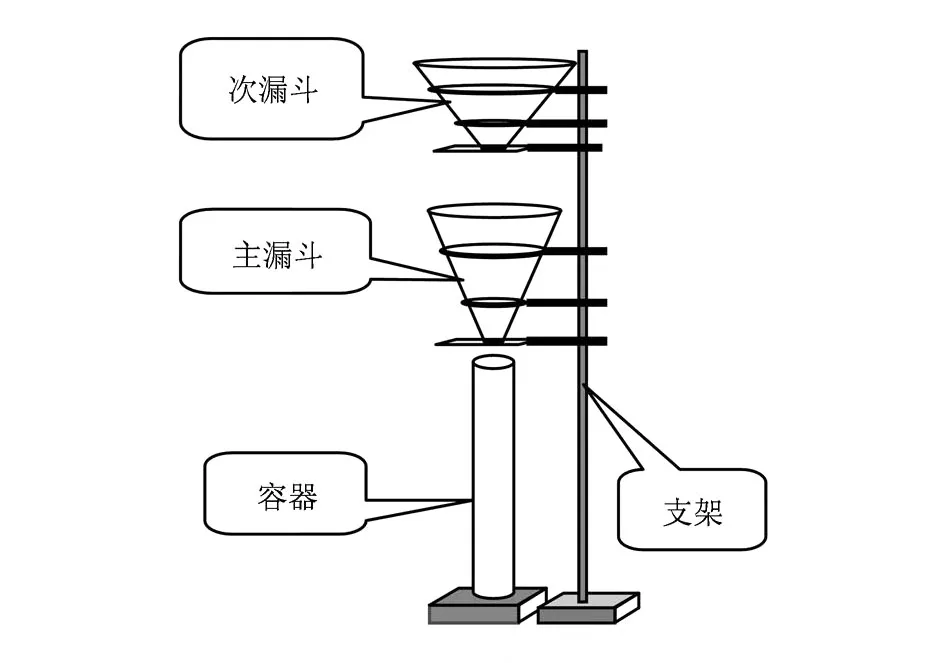
图1 实验装置示意图

我们用锥形漏斗制备颗粒堆,影响漏斗出料口流量和颗粒堆体积分数的因素很多,除了漏斗出料孔径D和颗粒直径d外,还有漏斗的形状;漏斗、颗粒及容器材料的弹性;容器壁与颗粒间以及颗粒与颗粒间的摩擦系数和静电作用;环境湿度和温度等等.我们实验的控制参量为出料孔径D和颗粒直径d.为了保证在相同的控制参量下测量结果的可重复性,除了控制参量可改变外,其他实验条件均相同.为保证各次测量中颗粒堆形成的历史相同,我们采用二级漏斗(锥形)制备颗粒堆(图1),先将颗粒以一定的流量填入次漏斗,然后控制颗粒从次漏斗流入主漏斗,最后再控制颗粒从主漏斗流入颗粒容器.其中,次漏斗出料口径D′固定不变,其值为D′= 1.60 cm;主漏斗的出料口径D可以改变,D的变化在0.45 cm到3.00 cm范围内;漏斗的锥角(漏斗的棱边与竖直线间的夹角)为6°,图2是制备颗粒堆的过程中不同粒径的颗粒堆质量m随时间t变化的实验数据(D=1.60 cm),数据表明,m随t线性增加,制备流量Q=m/t不随时间变化.

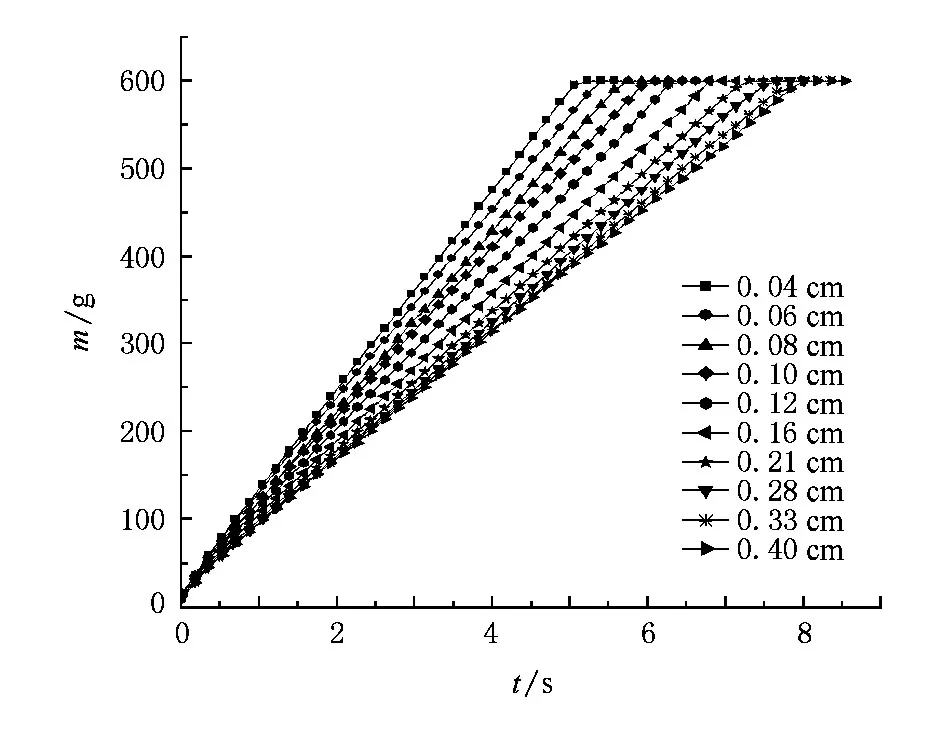
图2 制备过程中不同粒径的颗粒堆质量m随时间t的变化

实验中,制备颗粒堆的流量Q(单位时间填充的颗粒堆的质量)由电子秤间接测量,颗粒堆的体积分数η(颗粒堆的总质量除以颗粒材料的密度和颗粒堆的体积)由颗粒的密度,颗粒堆的质量及颗粒堆的高度间接测量,其中颗粒堆的高度由浦光JC4-10读数显微镜测量.

3.实验结果与分析

用不同出料口径D的漏斗制备粒径相同的颗粒堆,颗粒堆的体积分数η随漏斗的出料流量Q改变的实验数据及误差见图3(a),其中不同形状的实心点对应于不同的颗粒粒径.将实验数据用单调收敛饱和减函数

拟合,拟合曲线见图3(b),拟合参数ηu,ηd和γ见表1.结果表明:1)在粒径d一定的情况下,体积分数η随制备流量Q的增大而指数减少,增加和减少流量,颗粒堆的体积分数都会达到饱和,(1)式中ηu和ηd分别为体积分数的上限和下限饱和值.ηu和ηd都与颗粒粒径d有关,表1列出了不同粒径d对应的ηu和ηd值,其中ηu′和ηd′是相应的实验值.2)在Q一定时,(1)式中的γ越大则η越大,γ与粒径有关,表1列出了不同粒径对应的γ值,数据显示,粒径d越大γ值越大,γ对η的影响反映了粒径对η的影响,即在Q一定的情况下随着粒径的增大体积分数一般指数增大.3)ηu受D/d的比值影响较大,表1列出了粒径不同的颗粒堆其体积分数达到上限饱和值时对应的临界出料口直径Du与颗粒粒径d的比值,数据显示:Du/d>5.5时,ηu随粒径的增加而增大.相反,Du/d<5.5时,ηu随粒径的增加而减小,这意味着,Du/d小于临界值5.5时,随流量的减小,颗粒堆的体积分数增加明显变缓.4)在d>0.06时,ηd随d的增加而增大,然而,在d≤0.06 cm时,ηd随d的增加反而减小,这意味着,在d小于一定临界值时,随着流量的增加,颗粒堆体积分数的减小急剧变缓.

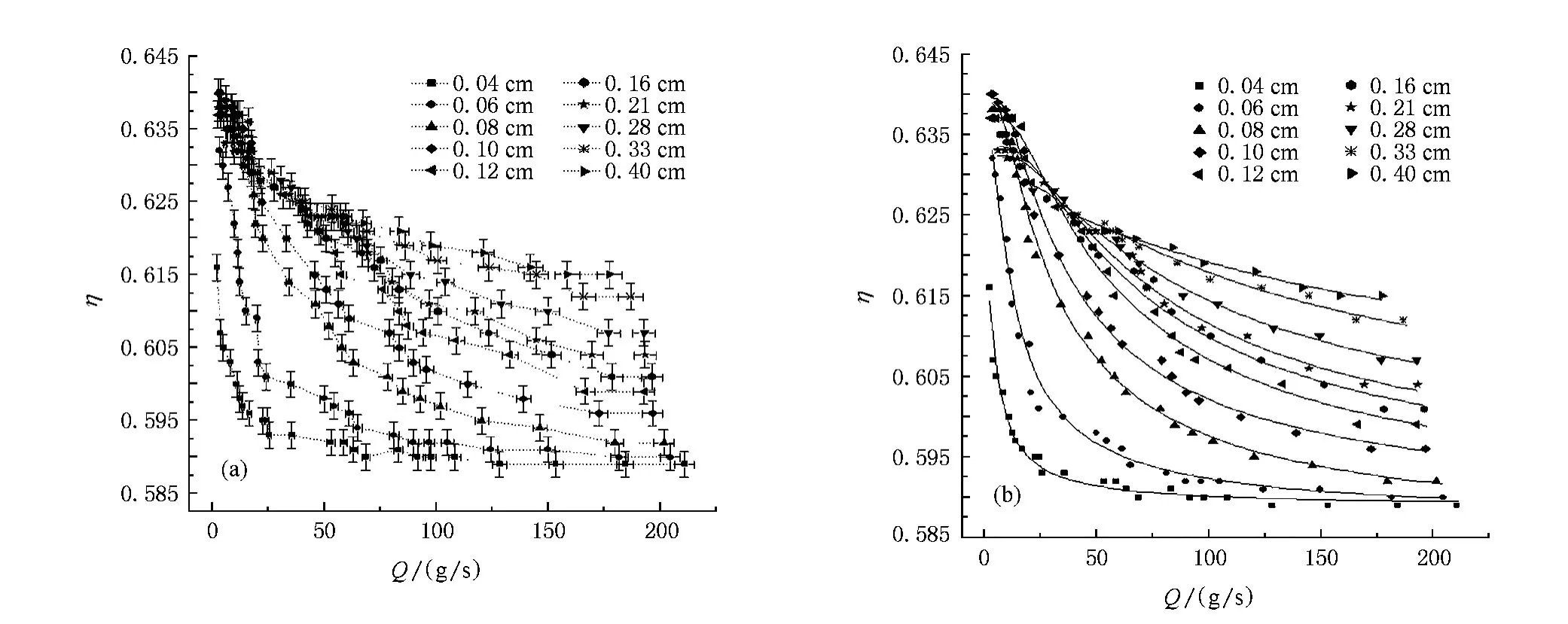
图3 不同粒径颗粒堆的体积分数与颗粒流流量的关系 (a)实验数据及误差;(b)实验数据的拟合曲线

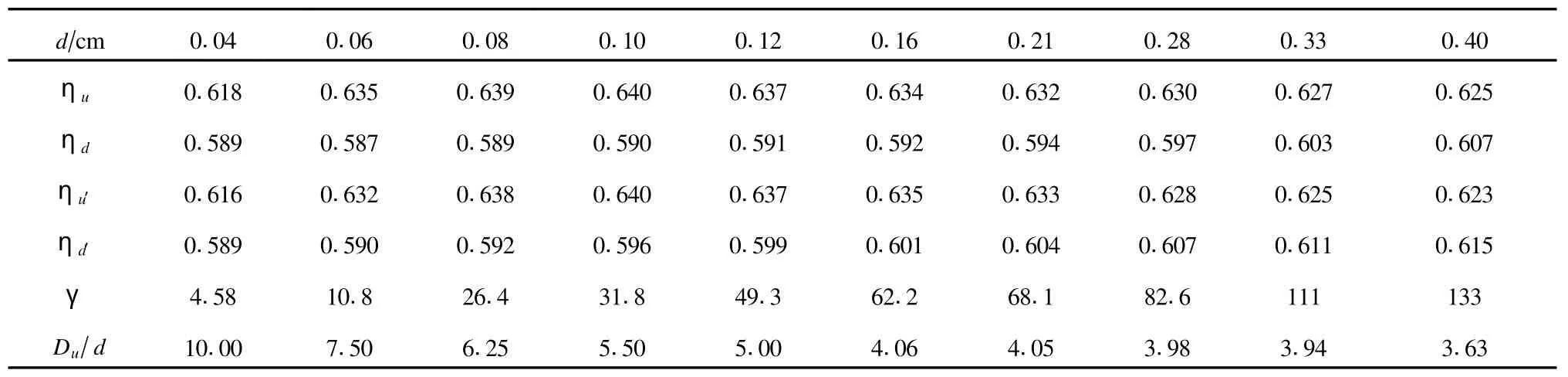
表1

粮仓效应告诉我们,当筒仓中颗粒堆的高度大于一定临界值(大约为筒仓直径两倍)时,筒仓底部受到的颗粒堆的压力不随颗粒堆的高度而改变,对于筒仓中较深的颗粒堆,大部分颗粒堆的重力被筒仓壁与颗粒间的摩擦力支撑,Jannsen用连续均匀介质模型较好地解释了粮仓效应[3,5,8],并得到广泛的认可.因此我们可以认为,筒仓中一定深度下,颗粒堆的体积分数(或颗粒堆的密度)不会因自身的重量而下面大上面小.然而筒仓中颗粒堆的体积分数却与颗粒堆形成的历史有关,我们认为颗粒堆形成的历史对颗粒堆体积分数的影响主要是颗粒流对颗粒堆的冲击以及颗粒物质的强耗散性对颗粒流冲击的衰减共同作用的结果.在制备过程中,前者使颗粒堆上部的密度由上至下增加,后者使颗粒堆受到的冲击由上至下减小,在颗粒堆表面一定深度(hc)下,冲击衰减到零,密度不再增加而稳定不变(以下将颗粒堆中稳定的密度用ρ表示).图4是制备颗粒堆的过程中不同粒径的颗粒堆高度h随时间t变化的实验数据(D=1.60 cm),其中直线是线性拟合线,结合图3的实验数据可见,颗粒堆的高度随颗粒堆质量的增加呈线性增长,这支撑了颗粒堆内部的密度可视为均匀不变的假设.图5显示了制备过程中,颗粒堆的密度及颗粒堆受到的冲击强度随时间的变化.对于结论1),用大流量制备颗粒堆,由于制备时间短,碰撞对颗粒流冲击颗粒堆的能量耗散很快(既有与颗粒堆的碰撞,又有与随后流下的大量颗粒碰撞),流到颗粒堆上表面的颗粒很快静止下来,这样,颗粒堆的结构相对疏松,因此体积分数较小.相反,用小流量制备的颗粒堆,由于制备时间长,颗粒堆对颗粒流冲击的能量耗散较慢,流到颗粒堆上表面的颗粒可以在上表面上反复跳跃多次,这对颗粒堆起到拍打致密的作用,导致颗粒堆的结构相对紧密,从而体积分数较大.由于无论制备颗粒堆的时间多短,颗粒堆受到的冲击被衰减得多快,颗粒堆总会有所致密,其密度总是比颗粒堆上表面处的密度大,因此颗粒堆的密度(或体积分数)随流量的变化存在下限饱和值ρd(或ηd).相反,无论制备时间多长,冲击的能量总会耗尽而不再对颗粒堆致密,颗粒堆的密度就不会再增加而达到饱和,因此颗粒堆的密度(或体积分数)随流量的变化存在上限饱和值ρu(或ηu).对于结论2),由于粒径d大则单位体积中颗粒数目少,碰撞中单位时间内能量耗散小,颗粒堆受到的冲击被衰减得慢,因此体积分数较大.对于结论3),我们认为主要是颗粒大小的因素与瓶颈效应的共同影响,虽然在流量一定的情况下,对于粒径d大的颗粒堆其体积分数一般较大,但是,当d增加到(D/d的比值小到)一定程度时,由于瓶颈效应[9—12],颗粒流从漏斗出料口流出的速度相对很小[13],这样,对颗粒堆的冲击致密的作用相应减小.由于D/d的比值越小,瓶颈效应越明显,因此会出现在流量Q(或D)一定的情况下,当粒径增加到一定程度,ηu会反而减小的现象,在我们的实验中,D/d<6时,有明显的瓶颈效应.对于结论4),我们认为主要是颗粒大小的因素与空气作用的共同影响,虽然在Q一定的情况下,粒径d大时体积分数一般较大,但是,当d小到一定程度时,用大流量制备颗粒堆,在颗粒堆快速致密过程中,颗粒堆中气体的压强波动较大,引起颗粒堆中一些疏松结构(如拱结构)坍塌,造成随着Q增加η的减小急剧变缓而趋于下饱和值,所以出现了d小ηd反而大的现象.在我们的实验中,d<0.06 cm时,空气作用较明显,这与文献[14]的结果d<0.05 cm时空气影响不能忽略较一致.下面我们从连续性原理出发推导颗粒堆的体积分数随制备颗粒堆的流量变化的拟合关系.

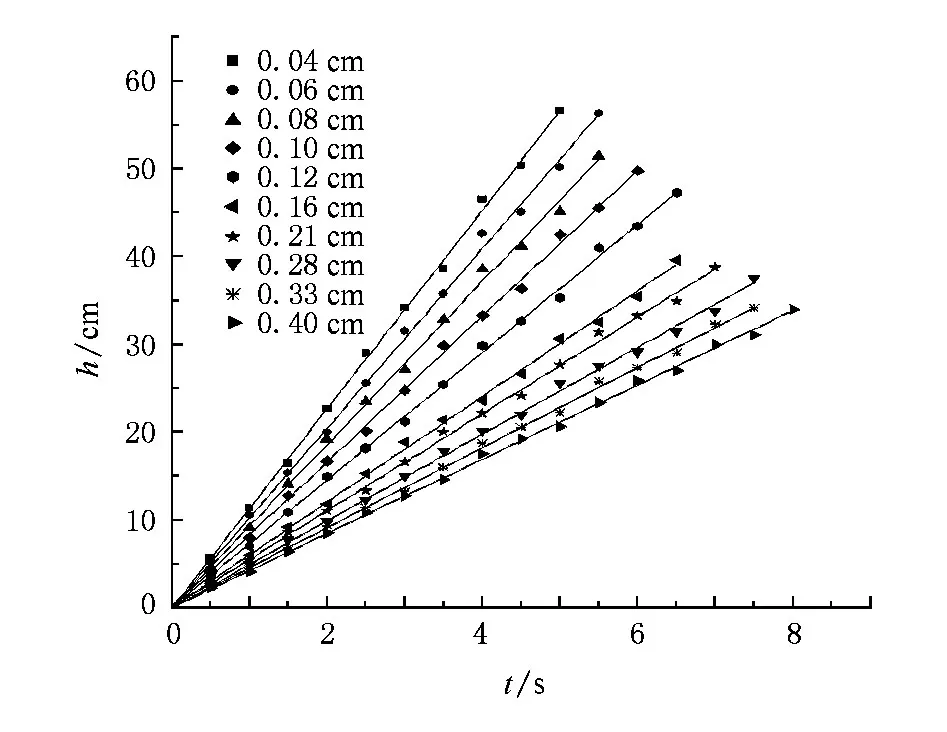
图4 制备过程中不同粒径的颗粒堆高度h随时间t的变化

在颗粒堆上部密度非稳定的区域,取一薄层小体积元,某时刻其堆积密度为ρt,在制备过程中颗粒流的冲击下,从上方流进小体积元的颗粒比从下方流出的多,根据连续性原理该体积元内的密度随时间增加,有

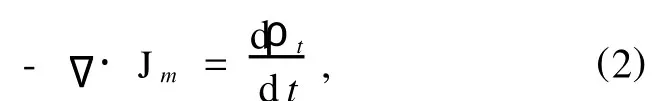
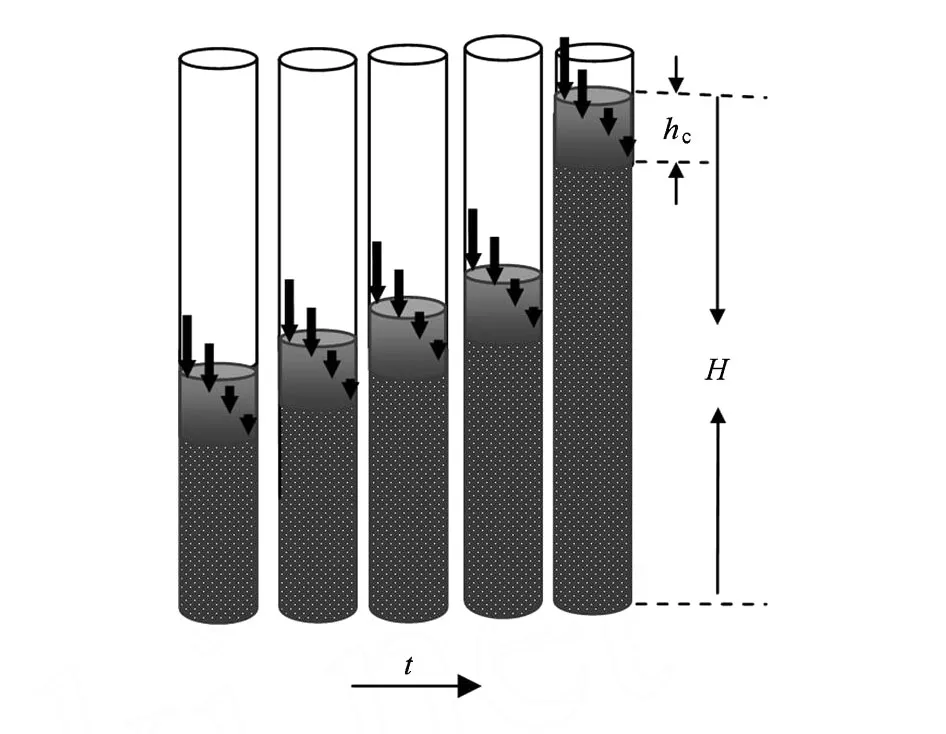
图5 颗粒堆的密度及颗粒堆受到的冲击强度随制备颗粒堆时间的变化(颜色的深浅表示密度的大小;箭头的长短表示颗粒堆受到的冲击的强弱;均匀白点表示密度均匀不变;下方向右的箭头表示时间增加的方向)

其中-Δ·Jm表示单位时间流进单位体积的净颗粒质量.另一方面由于碰撞对冲击能量的耗散,小体积元内的颗粒受到的颗粒流的冲击随时间减少.这样,小体积元的密度随时间在增加,受到的冲力又随时间在减小,因此单位时间流进单位体积的净颗粒质量一定随时间减少,也就是随密度增加而减小,假设单位时间流进单位体积的净颗粒质量随密度增加而线性减少,考虑到密度不会超过上饱和值ρu,将线性关系写成-Δ·Jm与ρu-ρt成正比,即

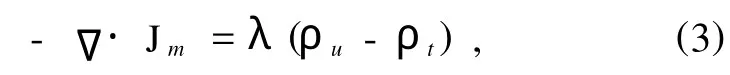
其中λ是比例系数,且λ>0.将(3)代入(2)有

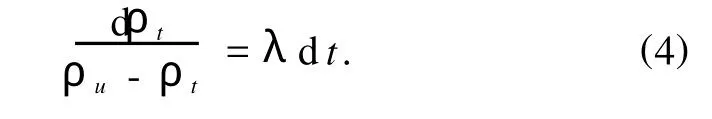
对上式两边积分,时间的积分限从小体积元位于颗粒堆表面时的0时刻到其密度稳定不变时的tc时刻,对应的密度积分限从ρd到ρ,得

实验中保证了制备颗粒堆的流量Q不随时间变化,总颗粒质量M相等,这样在制备颗粒堆的过程中使小体积元的密度由ρu到ρ的时间tc与制备颗粒堆的总时间T成正比,设比例系数为C,于是有

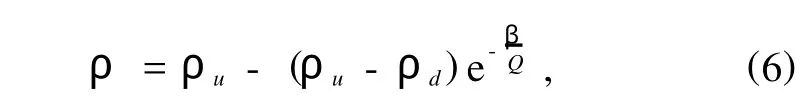
其中β=CλM,将上式两边除以颗粒材料密度得颗粒堆体积分数与流量的关系

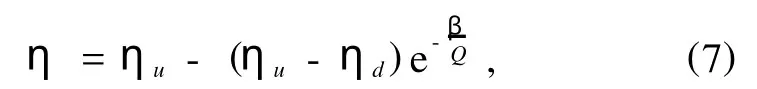
上式与实验数据的拟合公式完全相同.将表1中的体积分数的上限和下限饱和的拟合值ηu和ηd与实验值ηu′和ηd′进行比较可见,对于粒径d<0.08 cm的颗粒堆,体积分数的上限和下限饱和的拟合值与实验值都吻合较好;对于粒径d>0.06 cm的颗粒堆,体积分数的上限饱和的拟合值与实验值吻合较好,但体积分数的下限饱和的拟合值与实验值相差偏大.我们认为,由于拟合公式是在假设一定深度下颗粒介质连续均匀分布的条件下推出的,对于粒径d>0.06 cm的颗粒堆,将颗粒介质视为连续均匀介质还不够精细,这导致了拟合值与实验值比较的结果相差偏大.

4.结 论

颗粒物质的独特性质之一是颗粒物质的行为与它形成历史有关,我们通过实验探讨了颗粒堆的体积分数与制备过程中颗粒流流量的关系,结果发现,颗粒堆的体积分数随制备流量的增加指数衰减,减小和增加流量到一定程度时,体积分数都达到饱和;颗粒粒径小到一临界值时,体积分数随颗粒堆流量的增加减小明显变慢;出料口直径与颗粒粒径的比值小到一临界值时,体积分数随颗粒堆流量的减少增加明显变慢.我们认为颗粒流对颗粒堆的冲击以及颗粒堆的强耗散性对颗粒流冲击的衰减共同作用决定了颗粒堆的蔬密程度,对于颗粒粒径以及出料口直径与颗粒粒径的比值小到一定值时的临界现象分别是由于空气的作用和瓶颈效应的影响.我们从连续性方程出发推出的η随Q变化的函数与实验数据的拟合公式完全相同.颗粒物质广泛存在于自然界中,研究颗粒物质结构受其形成历史的影响有着重要的实际意义,如地震引起的堰塞湖决堤问题,堰塞湖的堤坝就是山体滑坡过程中形成的颗粒堆,地震的等级高低决定了山体滑坡流量的大小,影响了堰塞湖堤坝的疏松程度(或体积分数),地震等级越高,山体滑坡流速越快,堰塞湖堤坝越疏松,决堤的可能性越大,越有必要采取措施以减少对人类的威胁,颗粒物质的结构与制备流量关系的研究对防止自然灾害起着积极的指导作用.

[1]Vanel L,Howell D,Clark D 1999Phys.Rev.E 60 5040

[2]Vanel L,Clement E 1999Eur.Phys.J.B 11 525

[3]Lu KQ,LiuJ X2004Physics33 625(in Chiese)[陆坤权、刘寄星2004物理33 625]

[4]Hou M Y,Peng Z,Liu R,Wu Y,Tian Y,Lu K,Chan C K2005 Sci.Techn.Adv.Mater.6 855

[5]Duran J 2000Sand,Powder,and Grains(New Y ork:Springer)70-90

[6]kong W S,Hu L,Zhang X G 2007Acta Phys.Sin.56 2318(in Chinens)[孔维姝、胡 林、张兴刚2007物理学报56 2318]

[7]Hu MB,K ong X Z,Wu Q S,Wu YH2005Chin.Phys.14 1844

[8]Peng Z,Li X Q,Jiang L,Fu L P,Jiang Y M 2009Acta Phys. Sin.58 2090(in Chinens)[彭 政、李湘群、蒋 礼、符力平、蒋亦民2009物理学报58 2090]

[9]Hou M Y,Chen W,Zhang T,Lu K Q 2004Physics33 473(in Chinens)[厚美瑛、陈 唯、张 彤、陆坤权2004物理33 473]

[10]Bao D S,Zhang X S,Xu GL 2OO3Acta Phys.Sin.52 401(in Chinens)[鲍德松、张训生、徐光磊2003物理学报52 401]

[11]Bao D S,Zhou Y,Zhang X S,Tang X W2005Acta Phys.Sin.54 798(in Chinens)[鲍德松、周 英、张训生、唐孝威2OO5物理学报54 401]

[12]Bao D S,Lei Z M,Hu G Q,Zhng X S,Tang X W 2007Acta Phys.Sin.56 5922(in Chinens)[鲍德松、雷哲敏、胡国琦、张训生、唐孝威2007物理学报56 5922]

[13]K iwing T o,Pik YL,Pak H K2001Phys.Rev.Lett.86 71

[14]Yan X Q,Shi Q P,Hou M Y2003Physics.32 748(in Chinens) [阎学群、史庆藩、厚美瑛2003物理32 748]

PACC:4630P,4610,8220M

Experimental studdy on relation between volume fraction of sandpiles and flow rate of forming sandpiles＊

K ong Wei-Shu†Hu Lin Zhang Xing-Gang Yue Guo-Lian

(Key Laboratory for Photoelectric Technology and Application of Guizhou Province,School,Guizhou University,Guiyang 550025,China)

20 February 2009;revised manuscript

7 May 2009)

Thefunction of volume fractionηversus flow rateQwas determined.It is found thatηdecreases exponentially with increase ofQ.The volume fractionηwill reach saturation whenQis reduced or increased to certain extent.The increase ofη slows down rapidly with decrease ofQwhenD/ddecreases to a critical value.The decrease ofηslows rapidly with increase of Qwhenddecreases to a critical size.The phenomenon is explained by the dissipation of granules,effect of air,effect of bottleneck and collision theory.Theoretical result aboutη-Qis in agreement with the experimental result.

granular matter,flow rate,volume fraction

＊贵州省科技厅基金(批准号:20072003),国际合作项目(批准号:2007-400112),贵州省省长基金(批准号:2006-15)和组织部高层次人才特助基金(批准号:2006008)资助的课题.

†通讯联系人.E-mail:kongweishu@126.com

＊Project supported by the Foundation of Guizhou Province(Grant No.20072003),the International Collaborative Project(Grant No.2007-400112),the Province G overnor Foundation of Guizhou Province(Grant No.2006-15),the Organizational Department Foundation on the Excellent Talents(Grant No. 2006008).

†Corresponding author.E-mail:kongweishu@126.com