抗震设防烈度对钢框架连续性倒塌的影响1

石 磊 杜修力

（北京工业大学建工学院, 北京 100124）

抗震设防烈度对钢框架连续性倒塌的影响1

石 磊 杜修力

（北京工业大学建工学院, 北京 100124）

建筑结构在爆炸荷载作用下的连续倒塌问题近些年被很多学者所关注。从本质上讲，结构的抗倒塌和抗震都是动荷载作用下的结构响应问题，因此，结构抗震设计的很多理念对结构的抗连续倒塌设计同样适用。本文采用数值模拟的方法，分别对按抗震设防烈度Ⅵ度、Ⅶ度和Ⅷ度的钢框架结构进行了40kg炸药爆炸作用下的连续倒塌分析，探讨了抗震设防烈度对钢框架连续性倒塌的影响。计算结果表明，抗震设防烈度高的钢框架结构其抵抗连续倒塌的能力较强。其中，按Ⅵ度设防的结构发生了连续倒塌；按Ⅶ度设防的结构没有发生连续性倒塌，只发生了一定程度的变形和破坏；而相比之下，按Ⅷ度设防的结构变形和破坏最为轻微。

设防烈度 钢框架 连续倒塌 数值模拟

引言

近些年建筑结构在爆炸荷载作用下的连续倒塌问题被很多学者所关注（Song等，2000；Izzuddin等，2000；Berg等，2002；杜修力等，2008），许多国家都已将建筑结构在突发情况下的抗连续倒塌分析及设计方法编写进了设计规范（National Research Council of Canada，1975；Building Officials & Code Administrators International，1981）。而我国规范在这方面还是空白，研究成果也不多。

从本质上讲，结构的抗连续倒塌及抗震问题都是动荷载作用下的结构响应问题，因此结构抗震设计的很多理念对结构的抗连续倒塌设计也同样适用。本文使用结构设计软件ETABS，分别按Ⅵ度、Ⅶ度和Ⅷ度抗震设防设计了3栋钢框架结构。从抗震设防烈度对结构连续性倒塌影响的角度，采用数值模拟的方法，利用有限元软件 LS-DYNA分别对这 3栋钢框架结构进行了40kg炸药内爆炸作用下的连续倒塌分析，计算结果表明抗震设防烈度高的钢框架结构抵抗连续性倒塌的能力较强。按Ⅵ度设防的结构发生了连续倒塌；按Ⅶ度设防的结构没有发生连续性倒塌，但是发生了较大的破坏；而按Ⅷ度设防的结构，变形和破坏最为轻微。

1 钢框架的设计

为了研究按照中国结构设计规范设计出的钢框架结构在爆炸荷载作用下的结构响应，本文按照如下基本设计信息，设计了连续倒塌计算模型所采用的钢框架结构。

1.1 结构总体信息及设计参数

钢框架结构共4层作为商场使用。层高均为4m，X和Y两个方向梁的跨度均为6m。建筑场地为Ⅱ类场地，设计地震分组为第二组。

楼面活荷载：4kN/m2

楼面恒荷载：11.5kN/m2

地震荷载：抗震设防烈度为Ⅵ度、Ⅶ度和Ⅷ度，场地特征周期为0.4。

风荷载：基本风压为0.035 kN/m2，地面粗糙度为B类。

荷载组合：荷载组合和各分项系数均考虑《建筑结构荷载规范》规定的最不利荷载组合。结构材料为Q235钢和C30混凝土。

1.2 模型设计

计算模型依据我国的《建筑抗震设计规范》、《钢结构设计规范》和《建筑结构荷载规范》，采用国际通用的建筑设计软件ETABS进行设计。

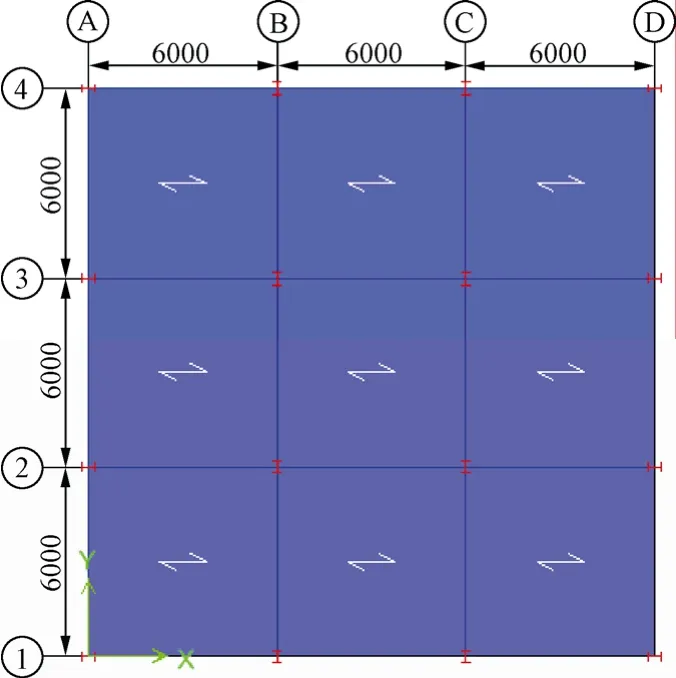
图1 标准层平面图Fig.1 Plane view of standard story

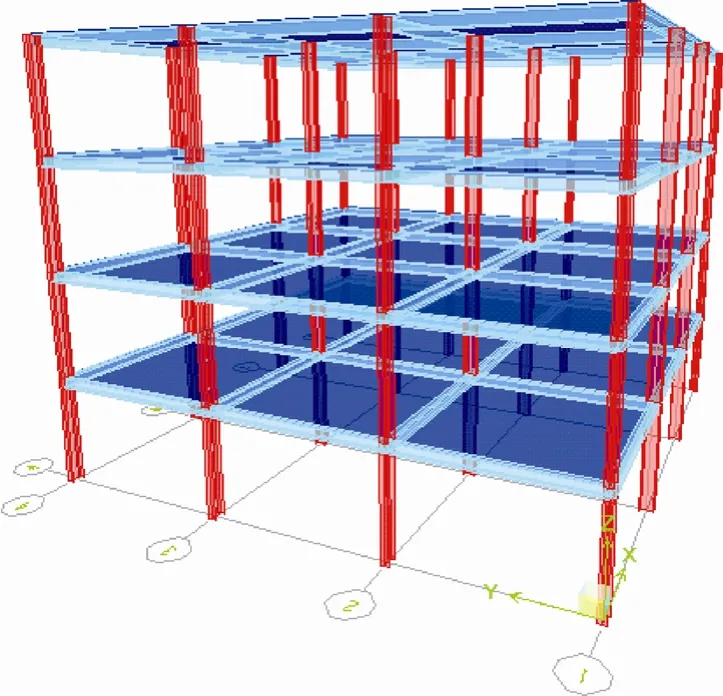
图2 三维结构图Fig.2 The 3-D sketch of the steel-frame

图1和图2为结构标准层平面图和三维立体图。经过计算框架梁柱采用焊接工字钢，考虑到施工安装问题，每个计算模型的框架梁、框架柱和楼板都没有改变截面。具体截面尺寸如表1所示，结构前五阶自振周期如表2所示。

表1 不同抗震设防烈度的钢框架构件截面尺寸Table 1 Sectional dimension sizes of structural member

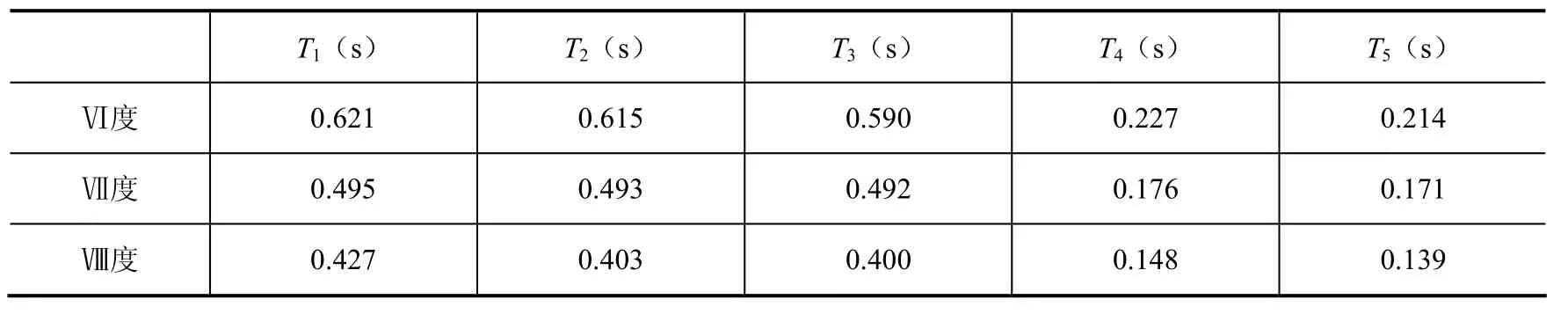
表2 自振周期对比Table 2 Comparison of natural vibration period

2 连续倒塌简化分析方法

美国总务局吸收了近些年结构连续倒塌的研究成果（Ronald等，2004；Anatol等，2003），出版了GSA（General Services Administration）规范（GSA，2003），该规范是现今常用的结构抗连续性倒塌设计规范。由于 GSA规范中的倒塌判定方法是根据美国结构设计规范及材料标准所制定的，因此在中国应用时存在很多问题。为此，本文采用显式有限元软件 LS-DYNA，使用一种简化的结构连续倒塌分析方法，对钢框架结构进行倒塌分析。在此方法中，利用简化的爆炸荷载考虑爆炸空气冲击波对结构构件的作用；利用可以考虑应变率效应的非线性梁单元模拟结构构件，通过设置屈服应力的方法考虑构件的破坏变形；通过设置失效应变和生死单元来考虑结构构件失效退出工作；通过设置结构构件及结构与地面之间的接触，来考虑结构构件在倒塌过程中的相互作用及荷载的向下传递。

2.1 结构单元

钢框架的梁及柱单元均采用二节点，每节点6个自由度的非线性梁单元来模拟，这种单元可以考虑材料及几何非线性，能计算大变形问题。楼板采用四节点板单元模拟。为节省计算时间，底板采用刚体单元。

2.2 材料模型

混凝土楼板采用双线性模型，并采用最大应变控制单元的失效。底板采用刚体模型。

梁、柱的材料本构模型采用 LS-DYNA中的 PLASTIC-KINEMATIC模型（Livemore Software Technology Corporation，1999），如图3所示。这是一种各向同性、随动硬化或各向同性和随动硬化混合模型。由于在结构倒塌时材料经常处于高速加载过程中，因此应考虑材料应变率对强度的影响，如图 4所示。在图 4中，σy0是正常加载条件下的材料应力-应变关系；σy1是高速加载条件下的应力-应变关系。应变率用Cowper-Symonds模型来考虑，用与应变率相关的因数表示屈服应力，具体形式为：

0tan切线模量；C、P为考虑应变率效应的参数。

在本文的计算模型中，相应参数的取值如表3所示。

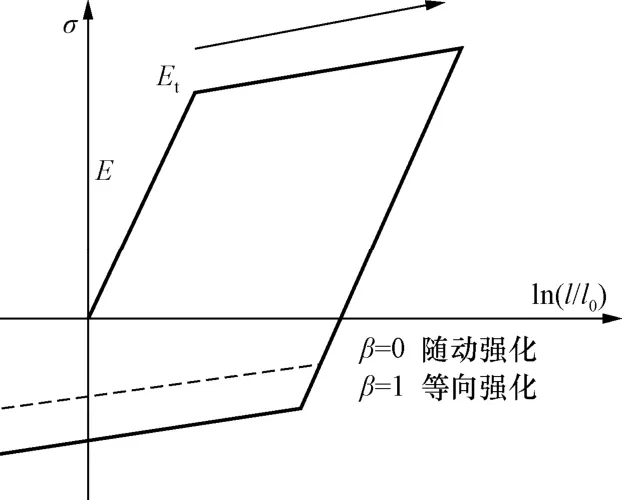
图3 PLASTIC-KINEMATIC模型Fig.3 PLASTIC-KINEMATIC model

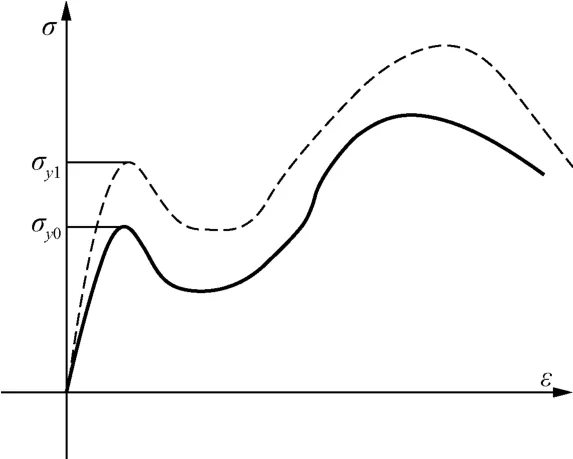
图4 应变率效应Fig.4 Curves of strain rate effect

表3 PLASTIC-KINEMATIC钢材材料参数Table 3 Parameters of PLASTIC-KINEMATIC steel material

2.3 爆炸荷载

本文考虑的是结构内爆炸问题。内爆炸的炸药当量一般不超过40kg，因此不会使整个结构产生整体性的破坏，但是主要被炸构件会被炸坏乃至失效。针对这一内爆炸的特点，本文考虑了主要被炸构件承受的爆炸荷载，由于其它结构构件承受的爆炸荷载比较小而没有加以考虑。将图5所示的爆炸冲击波荷载等效成被炸柱上的节点脉冲（图6），每个节点力的大小可以通过不同比例距离和入射角使用 TM5-1300手册（Department of the Army Technical Manual等，1969）上的经验曲线算得。

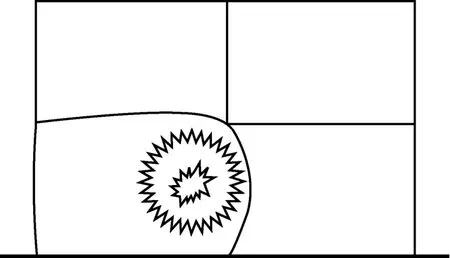
图5 爆炸荷载Fig.5 Explosive loading

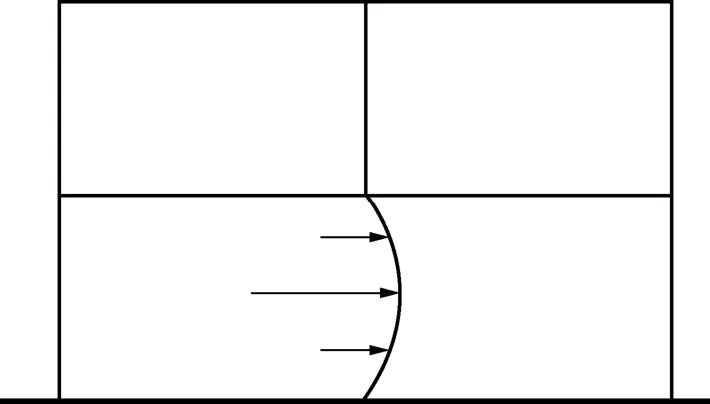
图6 简化的爆炸荷载Fig.6 Simplified explosive loading

2.4 结构倒塌过程的模拟

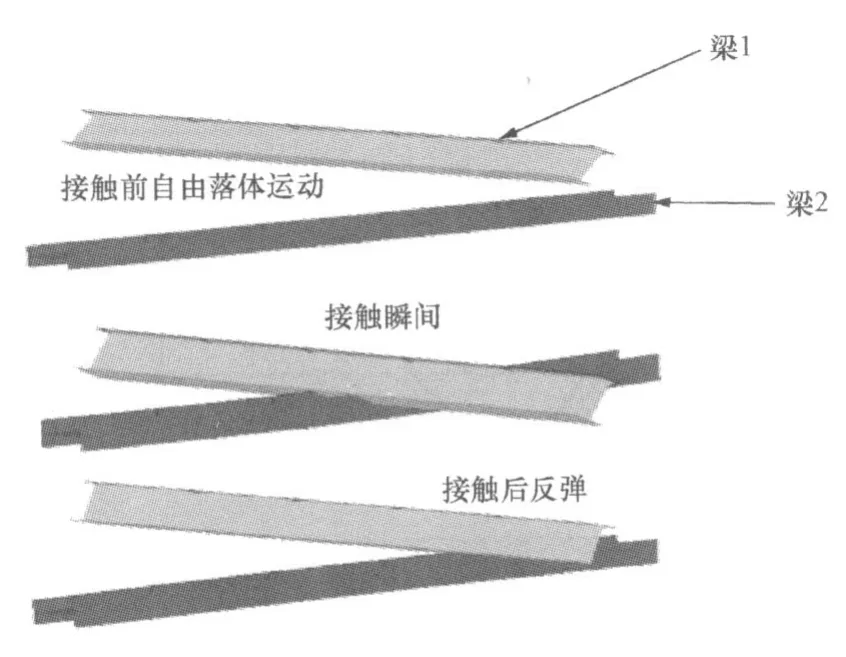
图7 梁单元接触过程Fig.7 Contact process between different beams

结构的倒塌是一个复杂的过程，其伴随着很多难以预测的受力及破坏状态。在美国规范中需要预测倒塌过程，并使用类似PUSHOVER一样的加载方法，因此其过程比较繁琐，在工程中不易应用。本文利用LS-DYNA软件强大的接触碰撞问题求解方法，通过设置结构构件及结构与地面之间的计算参数，来考虑结构倒塌过程中各构件之间的相互作用及荷载传递。

由于计算模型的梁、柱均为梁单元，为了验证接触设置的有效性，本文做了如图7所示的算例进行了验证。计算模型为2根工字钢梁单元，长均为5m，截面均为0.4 × 0.25 × 0.08 × 0.12，2根梁空间正交相距1m，净距0.675m，梁1在重力作用下呈自由落体，与梁2相撞，而梁2两端铰接，2根梁发生接触相互作用，系统无摩擦。计算结果显示，梁单元接触设置可靠。

3 数值计算

3.1 计算方法

本文采用动力松弛计算方法。在使用时首先要求计算系统在静力荷载作用下的静力稳定解，由于静力解是时步荷载瞬态响应的稳态部分，因而在自重作用下阻尼体系动力反应的稳态解，就是静力作用下的静力解，此时是应用动力方法求解静力问题。在静力稳定后，修改系统阻尼并添加非线性因素，继续进行计算（杜修力，2009）。

荷载施加如图 8所示。首先对结构每层施加如 GSA规范所述的静力荷载，即DL+0.25LL，其中：DL为结构恒荷载之和；LL为结构活荷载之和。同时，施加一个较大的结构阻尼，经过一定时间的震荡衰减，直到结构形成一个稳定的初始应力场以后，再将阻尼改为正常钢结构的阻尼，然后施加节点脉冲荷载，计算直至结构稳定。有限元模型如图9所示。

图8 荷载施加Fig.8 Loading time history

3.2 计算结果对比

在3个计算模型中，都是在0.1s时达到静载作用下的稳定状态，因此，从0.1s时开始施加节点脉冲荷载。

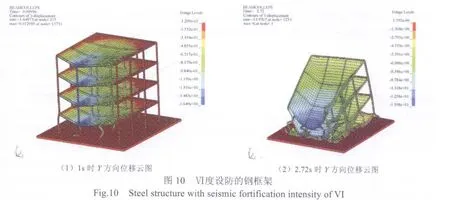
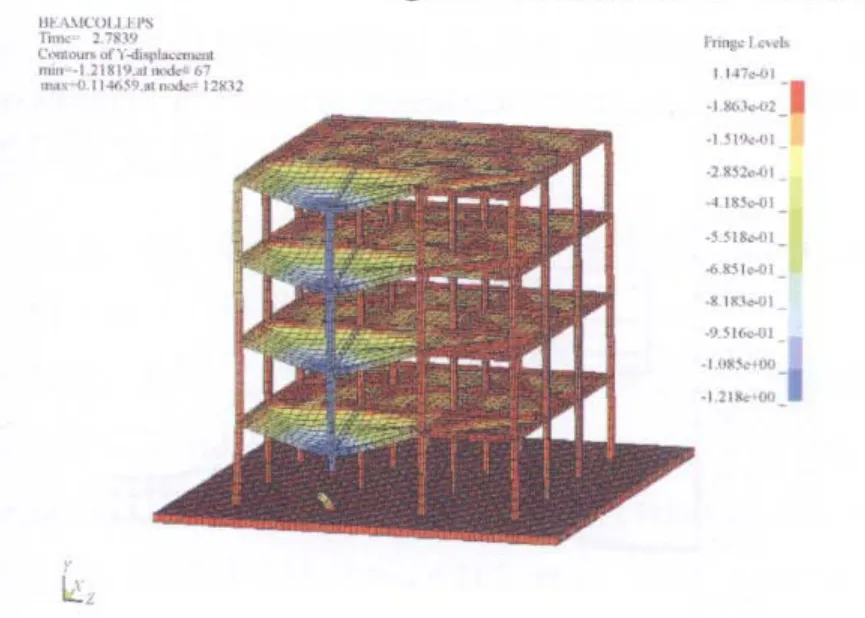
图11 Ⅶ度设防的钢框架Fig.11 Steel structure with seismic fortification intensity of VII

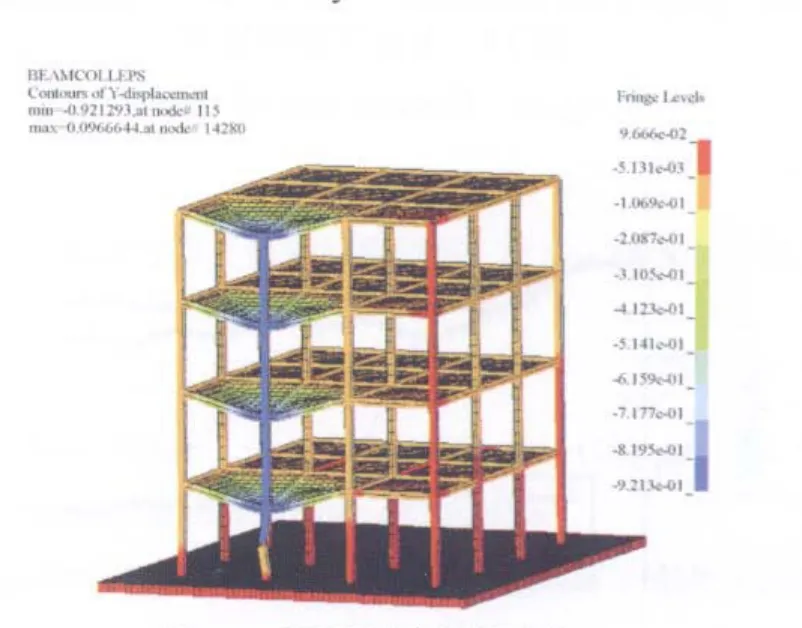
图12 Ⅷ度设防的钢框架Fig.12 Steel structure with seismic fortification intensity of VIII

图10为按Ⅵ度设防的钢框架结构Y方向的位移云图，在40kg炸药的爆炸荷载作用下，底层边柱被炸断，结构发生了连续性倒塌，并在2.72s时达到倒塌后的稳定状态。图11为按Ⅶ度设防的钢框架结构Y方向的位移云图，在40kg炸药的爆炸荷载作用下，结构没有发生连续性倒塌，但是发生了较大的变形及破坏。图12为按Ⅷ度设防的钢框架结构Y方向的位移云图，在40kg炸药的爆炸荷载作用下，结构底层边柱被炸断，没有发生连续性倒塌，结构的破坏程度轻于按Ⅶ度设防的钢框架。图13为一层数据提取节点的位置示意图，其中位置1为被炸柱所在的位置。图14为1节点Y方向的位移时程，按Ⅵ度设防的结构在爆炸荷载作用下，发生了连续倒塌，节点的竖向位移最大，基本等于楼层的层高；按Ⅶ度设防的结构在爆炸荷载作用下，没有发生倒塌，但是1节点发生了0.8m左右的竖向位移；按Ⅷ度设防的结构在爆炸荷载作用下，1节点的竖向位移为0.55m左右，破坏程度轻于按Ⅶ度设防。图15和图16为2节点和4节点的Z方向的位移时程，2节点和4节点的Z方向位移主要是由与其相连的梁的悬链线拉力所导致。从图15和图16可以看出，按6度设防的结构在爆炸荷载作用下，2节点和4节点所在的柱发生了压弯失稳破坏；而按Ⅶ度和Ⅷ度设防的结构在爆炸荷载作用下，由于柱子的侧向刚度比较大，没有发生压弯失稳。图17 为3节点X方向的位移时程，按Ⅶ度和Ⅷ度设防的结构在爆炸荷载作用下，在X方向的位移基本相同，可见这2栋结构在X方向的侧向刚度，完全可以抵抗框架梁传来的悬链线拉力。图18为1节点Y方向的速度时程，从图18可以看出，抗震设防烈度高的结构其变形及破坏的速度也相应较慢。

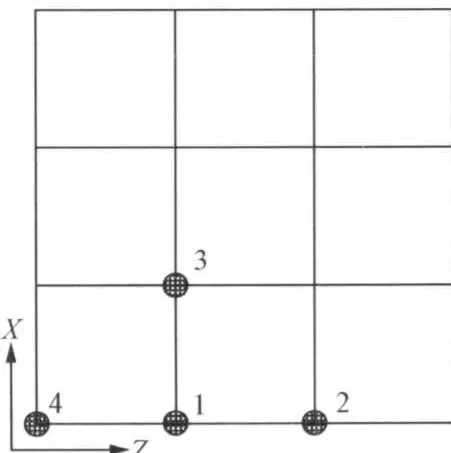
图13 节点平面位置图Fig.13 Position map of nodes

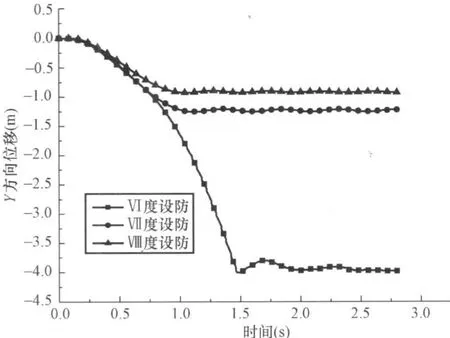
图14 1节点Y方向位移时程Fig.14 Displacement time history of node 1 in Y dimension

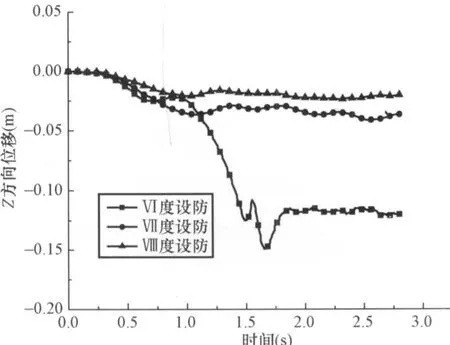
图15 2节点Z方向位移时程Fig.15 Displacement time history of node 2 in Z dimension

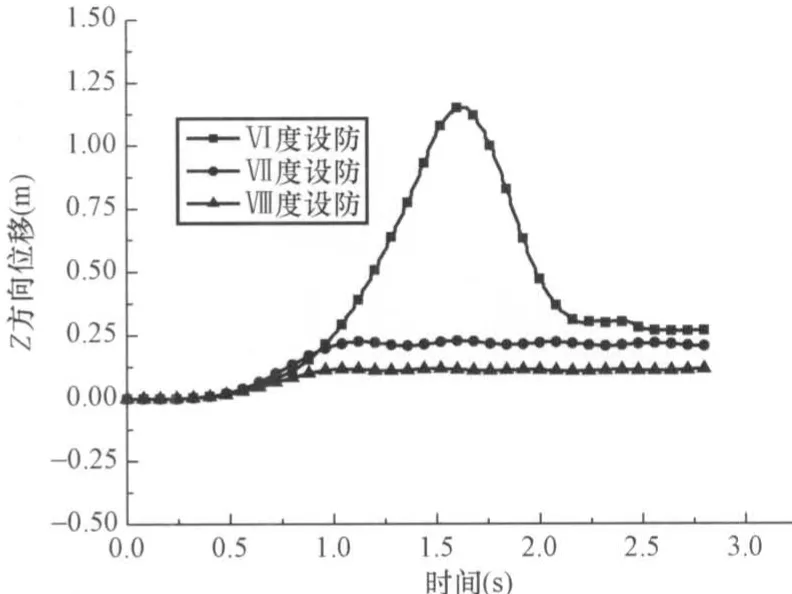
图16 4节点Z方向位移时程Fig.16 Displacement time history of node 4 in Z dimension

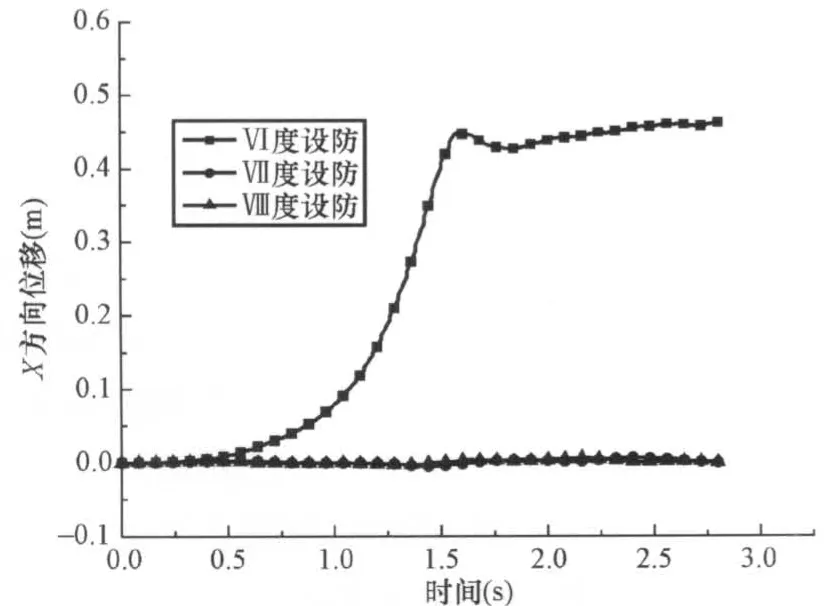
图17 3节点X方向位移时程Fig.17 Displacement time history of node 3 in X dimension

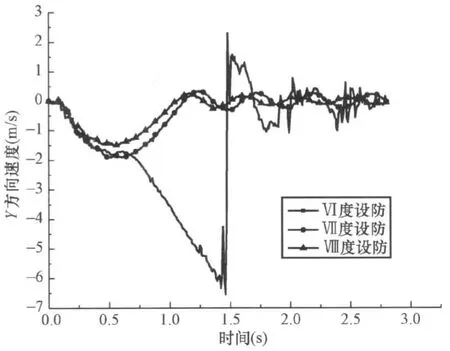
图18 1节点Y方向速度时程Fig.18 Velocity time history of node 1 in Y dimension

在本文的计算模型中，梁、柱及楼板之间的连接假定为理想的刚接，连接强度与构件等强。而在实际情况中，梁、柱及楼板之间连接的承载能力目前我们还不知晓，这还有待于进一步的研究。

4 结论

结构连续性倒塌往往是由于结构底层某根柱被炸坏后，丧失了承载能力，此时的结构荷载由与此柱相连的梁以弯矩、剪力的形式传递给与此柱相邻的柱子，导致相邻柱子上的轴向压力骤然增大。与此同时，与其相邻的柱子还要承受梁传来的越来越大的悬链线拉力。在这种综合的受力状态下，与被炸柱相邻的柱开始发生压弯变形，直至失稳破坏。按6度设防的钢框架结构就是在这种复杂的受力状态下发生了连续性倒塌；按7度和8度设防的结构，由于结构的侧向刚度较大，与被炸柱相邻的柱子具备相应的抵抗能力，而没有发生连续倒塌；按8度设防的结构变形及破坏均小于按7度设防的结构。由此可见，抗震设防烈度越高的结构，其抵抗偶然荷载激发的倒塌或破坏能力也越强。

杜修力，廖维张，田志敏等，2008. 爆炸作用下建构筑物动力响应与防护措施研究进展. 北京工业大学学报，34（3）：277—287.

杜修力，2009. 工程波动理论与方法. 北京：科学出版社，362—364.

Anatol L., Farid A., 2003. Blast resistant design with structural steel. Modern Steel Construction, 43 (10): 61—66.

Building Officials & Code Administrators International, 1981. National Building Code of America.

Berg V., Stofleth J.H., Preece D.S. et al., 2002. Analysis of dynamic loading of a simple structure to a blast wave. American Society of Mechanical Engineers, 435: 219—225.

Department of the Army Technical Manual，Department of the Navy Publication NAVFAC P-397, Department of the Air Force Manual AFM 88-22, Department of the Army et al., 1969. Structures to Resist the Effects of Accidental Explosion.

GSA, 2003. Progressive collapse analysis and design guidelines for new federal office buildings and major modernization project.

Izzuddin B.A., Song L., Elnashiai A.S. et al., 2000. Integrated adaptive environment for fire and explosion analysis of steel frames—Part II: Verification and application. Journal of Constructional Steel Research, 53 (1): 87—111. Livemore Software Technology Corporation, 1999. LS-DYNA Keyword User’s Manual (Version 950). Livemore Software Technology Corporation: 20.33—20.37.

National Research Council of Canada, 1975. National Building Code of Canada.

Ronald H., Andrew W., 2004. Design of steel structures for blast-related progressive collapse resistance. Modern Steel Construction, 44 (3): 45—51.

Song L., Izzuddin B.A., Elnashiai A.S., Dowling P.J., 2000. Integrated adaptive environment for fire and explosion analysis of steel frames—Part I: Analytical models. Journal of Constructional Steel Research, 53 (1): 63—85.

The Effect of Seismic Fortification Intensity on the Progressive Collapse of Steel-Frame Building

Shi Lei and Du Xiuli

( College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100022, China)

The progressive collapse of buildings under explosion has attracted lots of attention from researchers in recent years. Structural collapse resistance and seismic resistance essentially belong to same issue of structural response under dynamic loading. Therefore, some theories in structural seismic design are also applicable to the design to resist progressive collapse. By applying numerical simulation, we have conducted a series of analysis on the progressive collapse under internal explosion of explosive charges of 40kg to the steel-frame buildings within regions of the seismic fortification intensity of VI, VII and VIII degrees respectively, and then investigated the effect of seismic fortification intensity on the progressive collapse of steel-frame buildings. The results indicate that the steel-frame building within the region of seismic fortification of higher degree has stronger capacity to resist progressive collapse than those without fortification. In details, the building with VI of anti-seismic design collapsed, while the building with VII of anti-seismic design did not collapse, but suffered deformation and damage to some extent. In contrast, the building with VIII of anti-seismic design only had minor deformation and damage.

Seismic fortification intensity; Steel-frame; Progressive collapse; Numerical simulation

石磊，杜修力，2010. 抗震设防烈度对钢框架连续性倒塌的影响. 震灾防御技术，5（2）：176—184.

国家自然科学基金重点项目（50638030）；国家“十一.五”科技支撑项目（2006BAJ13B02）

2010-01-15

石磊，男，生于1979年。博士生。主要研究方向：结构抗震。E-mail: stonel@yeah.net