基于LMI的刨花板施胶鲁棒H∞控制1)

郭继宁 朱良宽 孙丽萍

(东北林业大学，哈尔滨，150040)

在刨花板的工业生产中，施胶量的多少以及施胶的准确性和均匀性直接影响着产品的质量和成本［1］。为达到按配方要求准确配比和按比例均匀施胶，近年来，国内一些科研机构和企业在刨花板施胶控制技术方面开展了多项研究。例如文献［2］、［3］对调施胶应用技术进行了研究，通过分析调施胶工段的组成，对如何提高调施胶设备和应用技术水平，提出了新的看法，重点论述了PID控制和模糊自适应控制技术;文献［4］中采用了先进的并行在线施胶工艺和设计，以及与工艺相适应的设备及控制系统等［2－4］。然而，文献［2］－［4］控制的结果都是基于经验估计、非线性系统的线性化、忽略干扰因素的情况下得出的。对于实际生产过程中的施胶系统，系统模型的不确定性和系统的一些干扰因素都无法忽略，因此以往的控制方法很难达到施胶系统的工艺要求及某些期望的性能指标。笔者针对上述问题，基于系统辨识出的施胶系统数学模型，并针对由设备老化、振动等因素引起的外界干扰及模型不确定性，采用鲁棒H∞控制理论设计鲁棒控制器，将其转化为线性矩阵不等式(Linear Matrix Inequality，LMI)问题求其可行解，最后通过仿真对设计控制器的性能和控制品质进行了验证。

1 刨花板施胶系统工艺及模型

刨花板施胶控制过程首先是设定刨花与胶液的配比，然后根据刨花流量的大小，确定施胶量;通过电磁流量计计量检测施胶流量，并反馈控制施胶电机转速，使施胶量随刨花流量的变化而改变。

图1为一种比较常用的刨花板施胶流量闭环控制流程图。流量测量是将电磁流量计测量值和控制器的期望值进行比较，把误差送给控制器，控制器为了保证误差最小，需要不断地调整电机转速，从而达到不断减小理想值与实际值之间误差的目的。

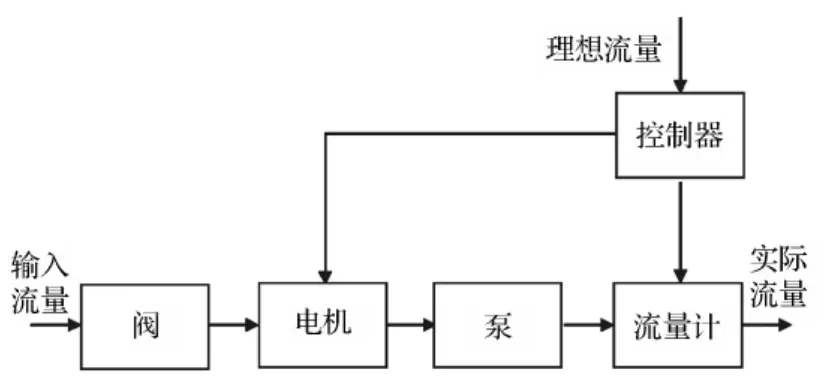
图1 刨花板施胶流量闭环控制流程

根据刨花板施胶过程的控制要求和流量范围，其控制结构可能存在不同的动态特性。实际中的施胶系统开环特性是一个非线性系统，它的稳态增益和阶跃响应随着流量大小的变化而变化。然而，当流量在某一固定值附近小范围变化时，刨花板施胶系统可以近似看作线性系统。

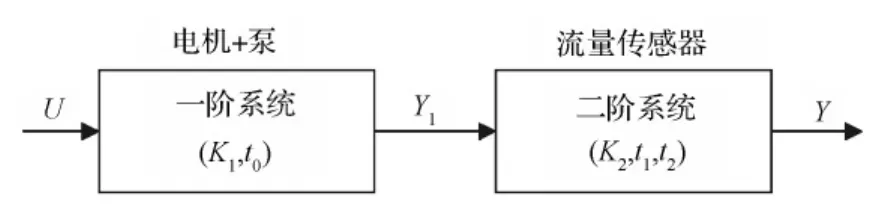
图2 简化的施胶控制系统开环模型结构

由于刨花板施胶过程工艺变化导致流量变化很大，故其开环系统控制模型一般在2～4阶变化［5］。图2为常用的开环模型结构，其中U代表电机的输入电压，Y1代表和流量传感器的流量比例对应的电压值，Y代表传感器的流量输出。K1和K2为系统的稳态增益，τ0、τ1和τ2为系统的时间常数。这样的系统结构要根据实际设备的动态特性及工艺的变化进行调整，系统的传递函数表达式如下所示:

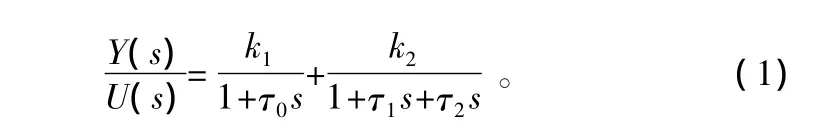
2 基于LMI的鲁棒H∞控制

假定系统的状态是可以通过直接测量得到的，那么可以根据要求设计一个静态的状态反馈器

使得相应的闭环系统

是渐进稳定的。如果使闭环传递函数Tzw(s)满足

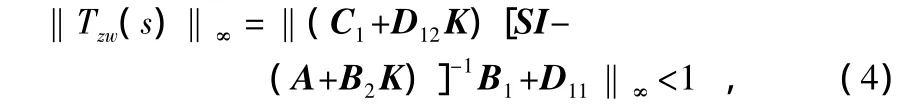
则称具有这样性质的控制律为闭环系统系统(2)的一个状态反馈H∞控制律。

设广义被控对象G的状态空间实现为

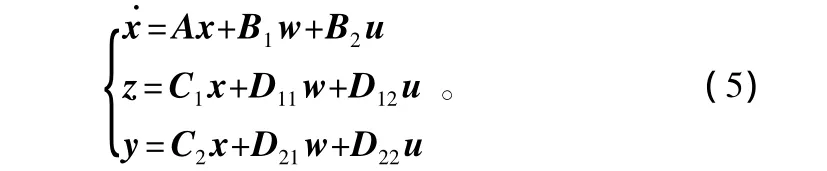
定理1:对于系统(4)，存在一个状态反馈H∞控制器，当且仅当存在一个对称正定矩阵X和矩阵W，使得以下的矩阵［6］

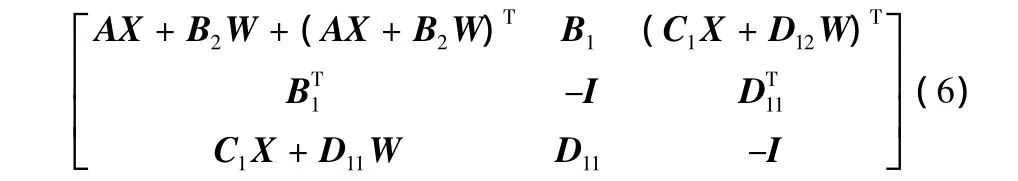
小于0成立。进而，如果矩阵不等式(5)存在可行解X*和W*，则

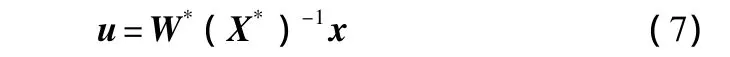
为系统(4)的一个状态反馈解。

根据以上原理，可为刨花板施胶系统设计满足一定性能指标的状态反馈控制器。

3 刨花板施胶鲁棒H∞控制器设计及仿真

3.1 干扰抑制问题转化为H∞标准设计问题

干扰抑制控制系统框图如图3所示。其中，G0为被控对象，K为控制器，v为参考输入，y为量测输出，d为外部干扰(量测燥声)，u为控制信号。为了对系统进行鲁棒控制，首先将其转化成鲁棒H∞的标准问题。

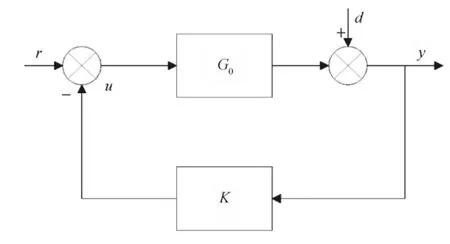
图3 干扰抑制控制系统

假设干扰信号d属于如下集合［7］:

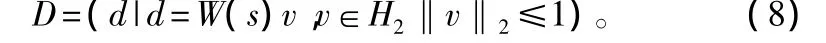
其中，W(s)是稳定的实有理函数，称为权函数，用来反映在期望频段上对干扰的抑制能力。

可知

所要求解的问题是设计控制器K(s)，使闭环系统内部稳定，并且使Tyv(s)W(s)v的H∞范数最小。图3干扰抑制控制系统中z=y，于是可以得出:

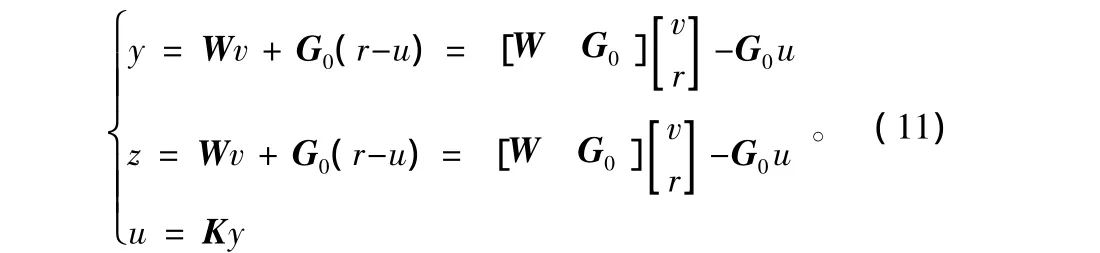
由此得出广义被控对象的传递函数矩阵为

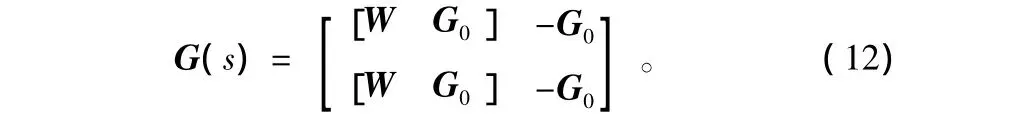
3.2 H∞状态反馈控制器的求解与仿真分析

在已有实验室设备基础上，通过德国Endress+Hauser流量计得到不同输入状态下流量值。应用Matlab系统辨识工具箱对模型参数进行估计。

在刨花板施胶的中频工况(输入25、30 Hz激励)，压力的变化对施胶流量的变化影响较大，致使流速在一定范围内波动，模型结构因施胶过程受外界扰动较多变得复杂，得到输出量与输入量之间的传递函数如下:

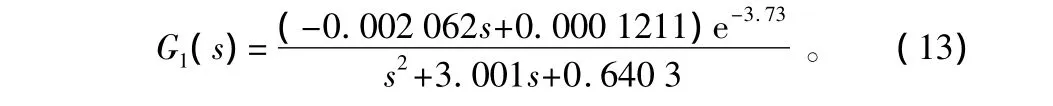
在输入干扰信号d情况下，得到输出量与输入量之间的传递函数为

根据公式(8)—公式(11)，可以推导得出上述传递函数的广义对象状态空间系数矩阵分别为

利用Matlab中LMI工具箱的相关命令函数feasp()求解可以得到系统的状态反馈矩阵为［8－10］:

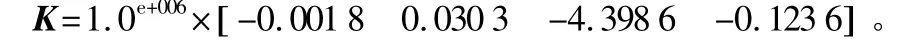
将鲁棒H∞控制器加入到控制系统中，得到系统的阶跃响应曲线如图4所示。

仿真结果可以看到:鲁棒H∞控制阶跃响应上升时间较快，超调量较小，系统响应的最大超调量为0.0556，稳定施胶时间4.2 s，所设计的控制器对施胶过程存在的外界干扰及模型结构不确定性具有很好的抑制作用，符合刨花板施胶的生产工艺要求。

图4 鲁棒H∞控制阶跃响应曲线

4 结论

在实际生产过程中，针对施胶系统存在的结构性和参数不准确性的问题，建立了基于实验数据的刨花板施胶模型，并在此基础上推导了系统的广义对象状态空间表达式。同时针对系统中由设备老化、振动等因素引起的外界干扰以及模型建立误差等问题，采用鲁棒H∞控制理论设计鲁棒控制器，将其转化为LMI问题求其可行解。最后，通过Matlab软件的LMI工具箱设计了刨花板施胶系统的鲁棒H∞控制器。通过仿真可以看出，所设计的鲁棒H∞控制器保证了系统的二次稳定，使控制系统指标达到了很好的效果，其响应上升时间较快，超调量较小的性能，符合刨花板施胶过程的生产工艺，为刨花板施胶的精准控制提供了一个很好的思路。

［1］陆仁书.刨花板制造学［M］.北京:中国林业出版社，1994:156－160.

［2］傅万四.人造板调供胶应用技术研究［J］.木材加工机械，2003(5):21－23.

［3］白崇彪，傅万四，曲闻远.刨花板施胶比自动控制模式研究［J］.木材加工机械，2007(1):33－35.

［4］花军，曹军，唐铉峰，等.纤维板的调施胶技术［J］.东北林业大学学报，2005，33(1):96－98.

［5］张丽.基于自适应遗传算法整定的刨花板施胶PID控制［J］.林业机械与木工设备，2008，36(7):42－44.

［6］俞立.鲁棒控制—线性不等式处理方法［M］.北京:清华大学出版社，2002:65－66.

［7］王德进.H2和H∞优化控制理论［M］.哈尔滨:哈尔滨工业大学出版社，1998:51－53.

［8］Hu Qinglei，Ma Guangfu，Xie Lihua.Robust and adaptive variable structure output feedback control of uncertain systems with input nonline-arity［J］.Automatica，2008，44(2):552－559.

［9］Lee J H.Memory less H∞controller for state delayed systems［J］.IEEE Tran Automat Control，1994，39(1):159－162.

［10］Gao Jianping，Huang Biao，Wang Zidong.LMI-based robust H∞control of uncertain linear jump systems with time-delays［J］.Automatica，2001，37(7):1141－1146.