改进自适应遗传算法在BP神经网络学习中的应用

李孝忠，张有伟

(天津科技大学计算机科学与信息工程学院，天津300222)

改进自适应遗传算法在BP神经网络学习中的应用

李孝忠，张有伟

(天津科技大学计算机科学与信息工程学院，天津300222)

针对遗传算法容易产生局值的问题，提出一种新的自适应遗传算法，改进遗传算子，通过比较两代之间的适应度评估值，选取适合的交叉率和变异率，保证了优秀个体进入下一代，而且避免了种群中最大适应度值的个体的交叉率和变异率为0的情况．最后，将改进后的算法应用于库存控制模型，实验表明，改进后的自适应遗传算法能避免局值，提高网络的收敛速度，改善了网络的学习性能．

BP神经网络；遗传算法；自适应

BP神经网络是一个黑箱模型，它具有很强的非线性映射能力、适应能力和学习能力，因此它的实际应用较为广泛[1]．但是BP 算法也有很多的缺陷，首先，BP算法的误差曲面通常都是凸凹不平的，会有多个极值点，易于陷入局部极值；其次，BP 算法的收敛速度慢，这与它的步长选择有关，步长取值大，则达不到精度，取值小则迭代步骤增加，收敛速度慢．当网络结构比较大时，这些缺点尤为明显．针对这些缺点，研究人员提出了很多对BP 算法的改进方案[2–4]，这些改进在一定程度上加快了收敛速度，但是，这些方法也有可能陷入局值，得不到最优解．

针对BP网络初始权值的选择问题，本文利用遗传算法来优化BP神经网络，利用它来学习神经网络的权值，并在自适应遗传算法的基础上改进遗传算子，根据适应度变化调节交叉率和变异率，并利用遗传算法的全局搜索能力对BP神经网络的初始权重进行自适应调整，最终得到一个优化的BP神经网络．

1 BP算法和遗传算法

1.1 BP网络和BP算法分析

BP 神经网络是一种具有三层或三层以上的单向传播的前馈多层神经网络，BP算法的基本思想是最小二乘算法，它采用梯度搜索技术[2]，学习过程是调整权值，以使网络的实际输出值与期望输出值之间的误差均方值最小．

BP三层神经网络包括输入层，隐含层和输出层．输入层有m个输入节点(X1，X2，…，Xm)，隐含层有q个节点(Z1，Z2，…，Zq)，输出层有L个输出节点(Y1，Y2，…，YL)，wij是输入层和隐含层节点间的连接权值，Wjk是隐含层和输出层节点间的连接权值．θj为隐含层第j个节点的阈值，f1和f2为隐含层和输出层的作用函数，f1可以选择非对称型Sigmoid函数f1＝1(1+e−x)，f2可以选择线性函数，d为期望输出值．以第t个输入样本为列，yk为输出层第k个神经元的输出函数，xk为输出层第k个神经元的输入函数，yj为隐含层第j个神经元的输出函数，L为隐含层第j个神经元的输入函数，η为学习速率，χ为平滑因子，0＜χ＜1．

1.2 遗传算法

遗传算法是建立在自然选择和遗传学机理上的一种搜索算法，该算法采用迭代寻优，着重解决现实中的优化问题[5]．遗传算法的操作对象是种群，每个种群有若干个染色体组成，每一个染色体对应于问题的一个解，由一个初始种群出发，采用基于适应度的选择策略在当前种群中选择个体，使用复制、杂交和变异方法产生下一代种群，如此一代代不断向最优解方向进化，最后得到满足某种收敛条件的最适应问题的最优解．遗传算法包含5个基本要素：参数编码，初始化种群，选择适应度函数，设计遗传策略，设定控制参数[6]．

2 自适应遗传BP神经网络的算法设计

2.1 自适应遗传算法

在遗传算法中，由于交叉率和变异率的值是固定不变的，不能根据当前已进化的状态取值，容易出现过早收敛而得到局部最优解的现象[7]，Srinvivas等[8]提出了一种随适应值变化的遗传策略——自适应遗传算法，交叉率Pc和变异率Pm能够随适应度自动改变．当种群各个体适应度趋于一致或者趋于局部最优时，使Pc和Pm增加，而当群体比较分散时，使Pc和Pm减少．同时，对于适应值高于群体平均适应值个体，对应于较低Pc和Pm，使该个体可以进入下一代；而低于平均适应值个体，对应于较高Pc和Pm，使该个体被淘汰，因此它能提供对某个解最佳的Pc和Pm．自适应遗传算法能够在保持群体多样性同时，保证遗传算法收敛性．经过改进，Pc和Pm的表达式为

式中：fmax为群体中最大的适应度值；fav为每代群体的平均适应度值；'f为要交叉的两个个体中较大的适应度值；f为要变异个体的适应度值；Pc1为固定最大交叉率；Pc2为固定最小交叉率；Pm1为固定最大变异率；Pm2为固定最小变异率．

2.2 改进的自适应遗传算法

由式(6)和式(7)可以看出，在这个算法中，适应度小的个体的变异能力较低，容易产生停滞现象．适应度高的个体得到了保护和推广，但是它的个体数目不宜过大，否则同样会使种群进化陷入停滞不前，造成局部收敛．为此，本文对交叉率Pc和变异率Pm进行了改进，提出了一种新的自适应遗传算法．引入两个参数1F和F2：式中：fmax为群体中最大的适应度值；fmin为群体中最小的适应度值；fav为每代群体的平均适应度值；g为遗传的第g代，g∈[1,G]；G为进化的总代数．

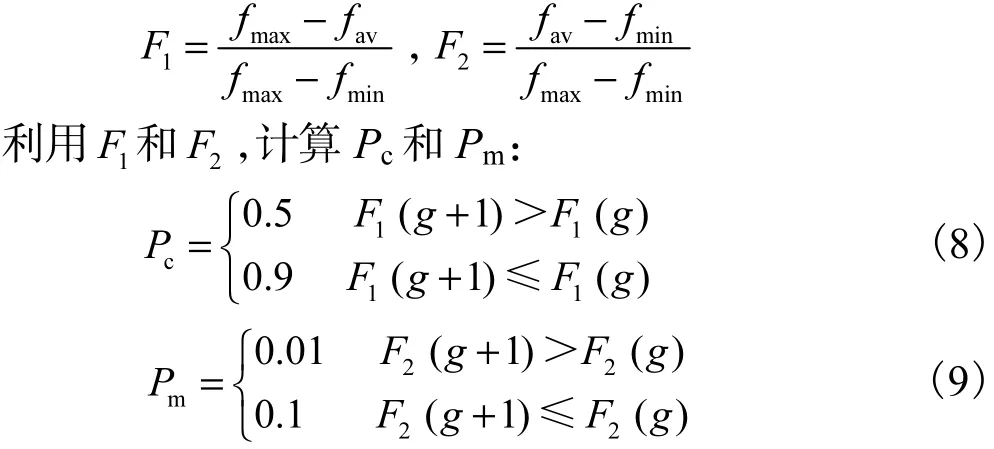
这种算法的思想是比较两代间的适应度值，先把第g代的适应度值用归一化的方法作处理，得到第g代适应度的评估值F1(g)，用同样方法得到第g+1代的评估值F1(g+1),比较这两个值，若F1( g+1)1＞F1(g)，说明适应度有提高的趋势，这时可以减小交叉率和变异率，保护优秀的个体进入下一代，反之，则说明之前的调节过度或者个体本身较差，应增大交叉率和变异率．可以看出，改进后的交叉率和变异率不但能够随适应度自动改变，而且避免了种群中最大适应度值的个体的交叉率和变异率为0的情况，这就相应地提高了种群中表现优秀的个体的交叉率和变异率，使得它们不会处于一种近似停滞不前的状态，从而使算法跳出局部最优解．

2.3 改进自适应遗传和BP神经网络结合

遗传算法和神经网络的结合主要是用遗传算法优化神经网络，即优化网络的权值和优化网络的拓扑结构，本文主要研究遗传算法对初始权值的优化．

利用改进自适应遗传算法的全局搜索能力对BP神经网络的初始权值进行自适应调整，最终可以得到一个优化的BP神经网络．将所要构建的BP神经网络的所有权值作为一组染色体，采用实数编码方式，选择适应度函数．当改进自适应遗传算法的网络误差满足一定条件后或进化数达到预先设定的参数，停止迭代，将得到的最优权值传递给神经网络，输入样本进行神经网络的再次训练．图1为基于遗传算法的BP神经网络学习流程图．

图1 遗传BP神经网络算法流程图Fig.1 Folw chart of the genetic BP algorithm

改进自适应遗传算法与BP神经网络结合的具体步骤如下：

(1)编码方式，权值和阈值采用实数编码，初始权值和阀值要求比较小，一般取(0，1)之间的数，其他输入数据作归一化处理．样本归一化公式为

式中：x为输入样本；xmax和xmin分别为输入样本的最大值和最小值；d为不大于1的常数．

(2)选择策略是比较个体的适应度函数值，利用转盘赌法从父代染色体中选取相同数目的染色体组成新的染色体群．

(3)染色体表示的各权值和阀值代入BP神经网络，训练样本集的输入和输出，得到误差E，若误差符合要求则停止训练，否则进行下一步．

(4)根据适应度进行自适应交叉和变异操作，选择合适的群体和交叉变异因子，进行遗传操作．实数编码的交叉方式为

式中：x1和x2表示相邻的两个父代；y1和y2表示相邻的两个子代；d为小于Pc的常数．

(5)根据遗传操作的结果，判断是否满足终止条件，若符合则程序结束，否则转向步骤(4)．

3 实 例

以某汽车生产企业的某种零配件成品10个月的库存量为例[9]，利用BP神经网络建立库存模型，用Matlab软件进行仿真预测．

将数据按月份分为10组，其中9组用于学习，1组数据用于预测．选取影响库存的9个因素为输入变量，通过调整最终选取9-8-1的BP网络结构，初始权重根据概率分布e−r确定[10]，学习次数为10 000次，允许误差为0.01，由于实数编码具有微调功能，不存在编码和解码的过程，所以采用实数编码方式，初始种群50，进化代数200，选择适应度函数f= 1E+1(E为误差函数)，Pc1＝0.9，Pc2＝0.6，Pm1＝0.1，Pm2＝0.001，Pc,min＝0.25，Pc,max＝0.5，Pm,min＝0.1，Pm,max＝0.5．影响库存因素的10组原始数据经式(10)处理后，得到归一化数据见表1，这里d的取值为1．经过训练，实验结果比较如图2所示．

从图2可以看出，传统的BP方法陷入了局值中；遗传BP算法开始时也陷入了局值，但在第490次训练后跳出；自适应遗传算法减少了训练次数和误差，它在进化的初期误差变化很小，如果设定的学习次数少或者允许误差大的话，就有陷入局值的可能；参数改进后的算法的误差一直在减少，所以不会选入局值，并且也减少了网络的训练次数和误差．

用第10组数据对训练结果进行测试，输入向量为[0.5，0.78，0.63，1，0.43，0.4，0.25，0.08，1]，在138次训练后误差满足要求，预测库存为0.1(3.4万件)，实际库存为0.13(3.5万件)，预测值接近实际值．

表1 影响库存因素的归一化数据Tab.1 Normalized data of stock influence factor

图2 库存问题几种BP算法结果的比较Fig.2 Comparison of several algorithm about inventory problem

4 结 语

本文针对传统BP算法收敛速度慢，易陷入局值的缺点，在自适应遗传算法的基础上对遗传算子进行改进，并把改进后的算法与BP网络相结合，优化权值，从而提高了算法的整体性能，减少了网络的训练次数，也较好地解决了BP网络容易陷入局值的问题．最后，用库存问题验证算法的有效性．

［1］汤素丽，罗宇锋. 人工神经网络技术的发展与应用[J].电脑开发与应用，2009，22(10)：59–61.

［2］张颖，刘艳秋. 软计算方法[M]. 北京：科学出版社，2002：174.

［3］穆阿华，周绍磊，刘青志，等. 利用遗传算法改进BP学习算法[J]. 计算机仿真，2005，22(2)：150–151.

［4］李影，徐涛，邢伟. 基于进化遗传算法的神经网络优化[J]. 长春理工大学学报，2006，29(3)：48–50.

［5］王小平，曹立明. 遗传算法：理论、应用与软件实现[M].西安：西安交通大学出版社，2002：73–74.

［6］高宏宾，焦东升，彭商濂. 一种基于遗传算法的改进的BP算法[J]. 计算机与现代化，2006(3)：6–8，13.

［7］曾凡超，朱征宇，邓欣，等. 车辆路径问题的改进的双种群遗传算法[J]. 计算机工程与设计，2007，28(20)：4998–5000.

［8］Srinivas M，Patnaik L M. Adaptive probabilities of crossover and mutation in genetie algorithms[J]. IEEE Transactions on SMC，1994，24(4)：656–667.

［9］刘婷. 基于神经网络和数据包络分析方法的安全库存预测及评价研究[D]. 重庆：重庆交通大学管理学院，2008.

［10］李敏强，徐博艺，寇纪淞. 遗传算法与神经网络的结合[J]. 系统工程理论与实践，1999(2)：65–69.

Application of Improvement Self-Adaptation Genetic Algorithm in BP Neural Network Learning

LI Xiao-zhong，ZHANG You-wei
(College of Computer Science and Information Engineering，Tianjin University of Science & Technology，Tianjin 300222，China)

A new self-adaptable genetic algorithm was put forward to solve the problem that it was easily to sink into the partial minimum in the genetic algorithm. By means of improving genetic operators and comparing the fitness value between two generations，the appropriate crossover rate and mutation rate can be selected to ensure the excellent individual into the next generation. And the situation that the largest population fitness value of individual cross-rate and mutation rate were zero can be avoided. Lastly，the improved algorithm was applied to the inventory control model. Results show that the improvement self-adaptation genetic algorithm can avoid sinking into partial minimum，enhance the convergence rate of the network，and improve the network study performance.

BP neural network；genetic algorithm；self-adaptation

TP183

：A

：1672-6510(2010)04-0064-04

2009-12-08；

2010-03-04

国家自然科学基金资助项目(70571056)

李孝忠（1962—），男，山东人，教授，博士，lixz@tust.edu.cn.