基于DFA方法的自组织组合预测模型的应用

叶学芳，何 跃

（四川大学 工商管理学院，成都 610064）

基于DFA方法的自组织组合预测模型的应用

叶学芳，何 跃

（四川大学 工商管理学院，成都 610064）

文章运用消除趋势波动分析（DFA）方法，计算了四川省工业增加值季度数据的标度指数，该指数表明四川省工业增加值的时间序列值具有长程相关特性，其预测模型有较好的拟合效果。在此基础上根据自组织数据挖掘的理论与方法，提出了自组织组合预测模型。模型预测结果及与ARIMA、GMDH自回归、SPSS曲线估计等三个单项预测模型及最优线性组合、人工神经网络组合等常用的组合预测模型的对比表明，自组织组合预测模型不仅改善了对数据样本的拟合精度，而且显著提高了模型的预测能力。

工业增加值；DFA；GMDH；ARIMA；自组织组合预测

0 引言

工业增加值是指工业企业在报告期内以货币形式表现的工业生产活动最终成果，是企业全部活动的总成果扣除了在生产过程中消耗或转换的物质产品和劳务价值后的余额，即企业生产产品或提供劳务过程中新增加的价值。四川省作为一个工业大省，工业增加值占据着GDP最大份额，在四川省的经济活动中起着举足轻重的作用。如何才能更有效准确地预测工业增加值，很多学者都提出了自己的看法。贾明辉等[1]应用灰色预测理论，建立灰色系统的预测GM（1,1）；张玲等[2]提出采用时间序列分析法对我国工业增加值的趋势进行预测；徐智勇等[3]利用支持向量机和微分进化算法相结合的方法对中国工业增加值数据进行预测；刘静思等[4]提出预测中长期工业增加值的一个有效方法是将AC模型、GMDH模型、SPSS曲线模型等三个单项模型进行最优线性组合预测；张秋菊等[5]选取AC模型、GMDH自回归模型、Curve Estimation过程预测等三个单项模型，再根据最小二乘法原理进行组合预测。前两位学者只采用了一种模型进行预测，后三位学者均采用了组合预测方法，结论中也证实了常见的组合预测模型的预测能力优于单项模型，但是是否存在更好的组合预测模型，使它的精度相比于常见的组合预测模型更高呢？针对这个问题，本文拟使用四川省2002～2008年工业增加值（现行价）实际数据，首先采用DFA方法用于探测工业增加值指标的时间序列分形标度特性与长期相关性；接着采用SPSS曲线估计、GMDH自回归、ARIMA等三个单项模型对工业增加值进行预测；然后分别采用最优线性组合预测模型、人工神经网络组合预测模型及自组织组合预测模型三种组合模型进行组合预测；最后比较分析各种组合预测模型的优劣。

1 DFA方法简介

消除趋势波动分析（DFA）方法自1994年由Peng等人提出之后，已成功地应用于许多领域，特别是在噪声序列、非平稳时间序列上DFA方法已成为广泛使用的技术。

对给定长度为 N 的序列{xk}（k=1，2，…，N），DFA 方法的一般过程如下[6～10]。

第一步：通过求和把原序列归并成一个新的轮廓序列

式中＜x＞是序列{xk}的平均值。

第二步：把轮廓序列y(i)分割成长度为s的Ns=int(N/s)个不相交的等长子区间。但因序列长度N通常不是分割跨度s的整数倍，一般对轮廓序列末端剩余的一小部分保留待用，若为了这一小段末端序列不至于被忽略，可以从原轮廓序列末端开始往回重复分割一次，这样就可一共获得2Ns个（当N为s的整数倍时，只要Ns个）等长子区间。

第三步：通过最小二乘法拟合每一子区间v(v=1，2，…，2Ns)上的局部趋势Pv(k)(j)函数，其中Pv(k)(j)是k阶多项式（k=1，2，…，N）（一般记为 DFA1，DFA2，…）。 消除子区间 v 中的局部趋势，得其消除趋势序列

第四步：计算2Ns个消除趋势子区间序列的平方均值

这里 v=1，2，…，2Ns，进而求这 2Ns个 F2(s,v)的均值的平方根

第五步：在双对数图中分析波动函数F(s)与s的关系

式中a为标度指数，它体现序列的相关特性。通常，波动函数值F(s)是分割长度s的增函数，做出logF(s)对logs的函数关系图，求出logF(s)相对于logs的变化斜率，其斜率即为所得的标度指数a。

当序列的标度指数a=0.5时，意味着该序列是一个独立过程，但并不能说明时间序列是一个高斯随机过程，仅表明序列不存在长期记忆。若时间序列仅是短期相关，a值会十分接近于0.5；当0.5＜a＜1时，暗示时间序列具有状态持续性；当0＜a＜0.5时，时间序列具有状态反持续性。特别地，当a=1时，时间序列的相关性与1/f噪声相似；若a＞=1，序列的相关性不再是幂律的形式；当a=1.5时，时间序列的相关性与布朗噪声相似。因此，标度指数a可以作为描述原始时间序列的“粗糙度”的指标，标度指数a越大，时间序列越光滑。

2 自组织组合预测方法

所谓组合预测方法，就是将不同的单个预测方法按照一定的原理进行适当的组合，综合利用各种单个方法所提供的有用信息，从而尽可能地提高预测精度。目前常用的预测方法分为权系数组合预测法和人工神经网络法。前者主要包括最优组合预测法和变权重组合预测法。它的缺点是当单个预测方法来源于非线性模型或者所基于的条件期望是信息集合的非线性函数时，各个单个预测方法的线性组合并不是最优的。而后者的缺点在于有时会造成过拟合现象。即模型对样本数据有较高的拟合精度，但预测能力差。为此，我们这里提出了自组织组合预测法。

最早的自组织数据挖掘思想——数据分组处理方法（GMDH）由A.G.Ivakhnenko于1967年首次提出，并成为自组织数据挖掘理论与方法发展的第一个里程碑。经过40多年的发展，如今在复杂系统的模拟、预测、模式识别、样本聚类等诸方面，自组织数据挖掘方法已经成为辅助人们进行系统分析和决策的强有力工具[11]。

自组织数据挖掘理论的基础是建立在人类生存历史中最古老的、最富有成效的试探法则——选择学说之上的。生物的遗传在不断地受到外界的制约并与周围的环境协调的过程中，物种将逐步发生变化。在大批量进行育种的过程中，为了得到新的一代，每一次大批量淘汰的过程都应该筛选出具有某些最好特性的，但还需要继续改进的那些生物，并利用这些生物继续育种。经过一些阶段的选择之后，就可以培育出理想的物种[12]。

表1 对四川省工业增加值求DFA标度指数过程

以参加组合的各预测方法作为自组织算法的输入，其输出即为组合预测结果，这就是我们提出的自组织组合预测方法。

3 实证分析

在进行DFA分析时，选取四川省工业增加值（现行价）2002年第一季度至2008年第四季度共28个数据作为研究对象。在后面的预测工作中，选取四川省工业增加值（现行价）2002年第一季度至2008年第四季度共28个数据作为训练集，选取四川省工业增加值（现行价）2009年第一季度至2010年第一季度共5个数据作为测试集 （数据均来源于四川省统计月报）。

3.1 DFA分析

从图1可以看出，logF(s)与logs之间存在着比较明显的线性关系。由于在第二步中从原轮廓序列末端开始往回重复分割了一次。因此，取s值为3～11的logF(s)与logs的数据，用线性回归求得标度指数a的值为1.103，a＞1，意味着四川省工业增加值时间序列具有持久性的长期相关，即工业增加值具有“长期记忆性”，过去的信息会影响到工业增加值未来的发展趋势。也就是说，工业增加值的数据是存在内部相关性的，数据是有效的。因此，可以通过自组织数据挖掘方法对工业增加值建立模型，用已知的工业增加值的数据预测未来一段时间内的工业增加值变化趋势是可行的[12]。即具有长程相关的时间序列，其模型有较好的拟合预测效果。

3.2 单项模型预测

3.2.1 ARIMA模型

图1 四川省工业增加值标度指数散点图

图2 二阶差分前序列图

图3 二阶差分后序列图

图4 二阶差分后的序列自相关系数和偏相关系数

差分自回归移动平均模型（ARIMA）是研究时间序列的重要方法，由自回归模型（AR模型）与滑动平均模型（MA模型）为基础“综合”构成。传统的趋势模型外推预测方法只适合于具有某种典型趋势性变化现象的预测，然而在现实中，许多现象的序列资料并不总是具有这种典型趋势特征，依此方法建立的模型所产生的误差项不一定完全是具有随机性质的，从而影响了预测效果。ARIMA模型先根据序列识别一个试用模型，再加以诊断，做出必要调整，反复进行识别、估计、诊断，直到适合的模型，因此它适用于各类的序列，是迄今最通用的时间序列预测法[13]。

这里我们采用Eviews6.0软件做ARIMA模型预测。以四川省工业增加值的季度数据为已知序列，绘制序列图，如图2所示。从图2可以看出，2002～2008年四川省工业增加值呈上升趋势，并且增长幅度不同，需进行平稳后处理。对原序列数据求对数后进行二阶差分转换后重新绘制序列图，如下图3所示。新序列无明显上升或下降趋势，说明通过二阶差分转换后的新序列具有稳定性。

对二阶差分转换后的数据做自相关和偏相关系数图，如图4所示。从图4中可以看出自相关系数在k=2与3时显著不为0，所以确定p值为1，2，3。偏相关系数在k=2时显著不为 0，所以确定 q 值为 1，2。因此（p，q）的可能组合有 6 个。表2为各个组合的参数值。其中AIC(Akaike info criterion)越小越好，SC(Schwarz criterion)越小越好，R-squared越大越好，通过比较这三个参数值，最后确定p值为2，q值为2。因为在数据处理时进行了二阶差分，所以d的取值为2。所以最终模型为 ARIMA（2，2，2）[14]。 最后得到的最终模型为：

其中，Z=ΔY。

3.2.2 GMDH自回归模型

GMDH自回归区别于一般回归模型的最大的优点是它将数据分为训练集和测试集，在训练集上使用内准则进行参数估计得到中间待选模型，而在测试集上使用外准则进行中间候选模型，而在测试集上使用外准则进行中间候选模型的选择，这个过程不断重复直到外准则值不能再改善才停止，这样的停止法则可以保证在一定噪声水平下得到数据拟合精度和预测能力之间实现最优平衡的最优复杂度模型，不会出现一般的回归方法中常出现的过拟合而牺牲了预测能力的现象[4]。

表2 ARIMA模型参数值

表3 SPSS各模型预测结果

表4 2009年1季度至2010年1季度工业增加值单项预测模型与组合预测模型预测结果

不同于SPSS，在做GMDH自回归预测时首先把工业增加值的季度数据转换为环比数据以消除量纲。然后通过在Knowledgeminer软件中不断调整参数并比较各参数值，最终筛选出最优复杂度模型如下：

其中：z11=6.359(e-2)Yt-2-6.895(e+0)

在模型拟合与预测中，R-squared的值越接近1，效果越好。此模型中为0.9769，十分接近1，拟合效果好；平均绝对百分比误差（Mean Absolute Percentage Error）越小越好，控制在5%以内均是可接受水平，此模型中为1.73%，误差小，可接受；预测误差平方和（PESS）越小越好，此模型中PESS=0.0286，预测误差较小。

3.2.3 SPSS曲线估计模型

用SPSS做预测可有很多种方法，可利用工业增加值与影响工业增加值的一些因素进行多元线性回归，剔除相关度低的影响因素，最后得到工业增加值与相关度高的各因素的回归模型。但利用此模型进行预测时，需要首先找出影响工业增加值的典型因素，并对各因素进行预测，才能对工业增加值进行预测，整个过程显得复杂，而且预测精度不一定高。也可以采用的自回归模型，但预测效果却不是很好。这里我们采用文献[4]提到的曲线估计模型。

首先选择分析→回归→曲线估计，将四川省各季度工业增加值的环比累加值作为因变量，将时间序列作为自变量，在模型一栏里选择常见的变量如线性、二次项、三次项、复合、幂等。表3即为SPSS各模型预测结果。

通过观察R Square的值以及经验分析，最后选定二次型模型为最优，即：

（注：在实际工作中，不一定只采用一种模型，可以对R Square值较好的几个模型求组合）

由于我们采用的是工业增加值的环比累加值进行预测，因此，式中的Yt为t季度工业增加值的环比累计值，Xt为t季度的时间序列值。

3.3 组合预测模型

3.3.1 最优线性组合预测模型

在SPSS17.0软件中将以上三个单项预测模型线性组合生成最优线性组合预测模型为：

3.3.2 人工神经网络组合预测模型

在matlab软件中编程将三种单项预测模型的输出YSPSS，YGMDH，YARIMA作为模型的输入，得到的人工神经网络组合预测模型为：

3.3.3 自组织组织预测模型

在knowledgeminer软件中，将三种单项预测模型的输出YSPSS，YGMDH，YARIMA作为模型的输入，用自组织数据挖掘技术筛选出的最优自组织组合预测模型为：

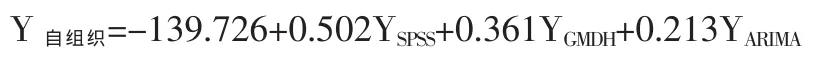
3.4 结果分析

四川省2009年1季度至2010年1季度工业增加值单项预测模型与组合预测模型的预测结果如表4所示。

从表4可以看出平均误差的大小顺序为：YARIMA＞YSPSS＞YGMDH＞Y最优线性＞Y人工神经＞Y自组织。 由此，可以得出组合预测模型的预测效果优于单项预测模型，而在三种组合预测模型中，自组织组合预测模型具有更好的预测效果。这是由于自组织组合预测模型充分发挥了自组织数据挖掘算法自身的特点和优点，在尽可能多的模型结构形式中进行择优选择，而不仅仅在线性形式中进行计算选择，这体现了复杂性科学研究的思想。自组织建模选择最适于系统的表现形式，从而尽可能地利用了每一单项预测方法的有用信息[12]。

4 结语

本文首先通过DFA分析得出四川省工业增加值是具有长程相关的时间序列，也就是说在预测时，其模型将有较好的拟合效果。然后采用三个单项预测模型和三个组合预测模型预测四川省2009年一季度至2010年一季度的工业增加值。实证分析表明，自组织组合预测模型无论是拟合效果还是预测精度都比单项预测模型及常见的组合预测模型高。

虽然自组织组合预测模型在数据拟合和预测方面整体精度都较高，但它是基于单项预测模型基础之上的。因此，提高各单项预测模型的拟合效果和预测精度，是提高自组织组合预测模型的预测能力的关键。

[1]贾明辉.我国工业增加值的灰色预测与分析[J].内蒙古民族大学学报（自然科学版），2009，24（2）.

[2]张玲.时间序列分析法对我国工业增加值趋势的预测分析与研究[J].统计与咨询，2010，（2）.

[3]徐智勇，孙林岩，郭雪松.基于支持向量机的中国工业增加值预测研究[J].运筹与管理，2008，17（3）.

[4]刘静思，何跃.基于组合预测模型的工业增加值中长期预测方法研究[J].工业技术经济，2008，（2）.

[5]张秋菊，何跃，马海霞，刘成昭.组合预测模型在工业增加值预测中的应用[J].统计与决策，2006，（9）.

[6]Peng C K，Buldyrew S V， Havlin S，et al.Mosaic Organization of DNA Nucleotides[J].Physical Review E，1994，49(2).

[7]Ausloos M.Statistical Physics in Foreign Exchange Currency and Stock Markets[J].Physica A，2000，（285）.

[8]Kantelhardt J W，Koscielny-Bunde E，Rego H H A，et al.Detecting Long-range Correlations with Detrended Fluctuation Analysis[J].Physica A，2001，（295）.

[9]Peng C K，Havlin S，Stanley H E，et al.Quantification of Scaling Exponents and Crossover Phenomena in Nonstationary Heartbeat time series[J].Chaos，1995，5（1）.

[10]Vjushin D，Govindan R B，Monetti R A，et al.Scaling Analysis of Trends Using DFA[J].Physica A，2001，（302）.

[11]贺昌政.自组织数据挖掘与经济预测[M].北京：科学出版社，2005.

[12]贺昌政，俞海，卢跃奇.自组织组合预测方法及其应用[J].数量经济技术经济研究，2002，（2）.

[13]刘明珠，赵晓萍，傅志华.灵活运用SPSS进行税收预测[J].中国发展，2005，（4）.

[14]腾格尔，何跃.基于GMDH组合的中国GDP预测模型研究[J].统计与决策，2010，（7）.

（责任编辑/亦 民）

F201

A

1002-6487（2010）23-0042-04

国家自然科学基金资助项目（70771067）

叶学芳（1987-），女，四川内江人，硕士研究生，研究方向：数据挖掘、管理信息系统。

何 跃（1961-），男，重庆人，副教授，研究方向：管理信息系统、数据挖掘、决策支持系统。