基于矩不变量的半脆弱图像认证水印算法研究
陈 萍,宋喜忠
(黄淮学院 计算机科学系,河南 驻马店 463000)
基于矩不变量的半脆弱图像认证水印算法研究
陈 萍,宋喜忠
(黄淮学院 计算机科学系,河南 驻马店 463000)
提出了一种新的半脆弱图像水印算法,该算法根据图像矩不变量的半脆弱性生成认证水印来区分偶然失真和恶意篡改,并由图像小波分解的逼近系数构成的水印来定位篡改区域.
信息隐藏;数字水印;图像认证
如何确保在网络环境下数字作品的完整性,是亟待解决的一个难题.为了解决这一难题,脆弱数字水印技术应运而生.脆弱数字水印分脆弱水印和半脆弱水印两种[1-4].目前几乎所有的半脆弱水印算法都不容忍几何变换,然而,在实际应用中一些几何变换是非恶意的.例如,旋转、缩放和平移都不会改变图像内容的真实性.在这种情况下,可以接受几何攻击的半脆弱水印算法研究就显得非常重要,具有实际意义.因此,本文提出一种基于矩不变量的半脆弱水印算法.
1 矩不变量及其半脆弱性分析
图像的矩和其不变量函数已被广泛应用到模式识别、特征提取、以及分类和识别领域.一幅灰度图像 f(x,y)的几何矩mpq,可定义为

中心矩μp,q可定义为
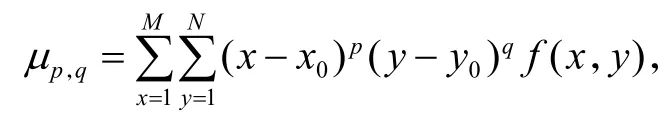
p,q表示阶数,x0=m1,0m0,0,y0=m0,1m0,0表示图像的质心,归一化中心矩ηp,A的定义为其中r=(p +q)2 + 1.
文献[5]推导出7个矩不变量,并指出这些不变量对正交变换具有不变性,如旋转缩放平移等.
Alghoniemy提出了一种基于几何矩的水印法[6],该方法侧重于算法的鲁棒性分析,不能完成认证中的检测和定位.Alghoniemy还采用数字水印对 Barbara图像进行了各种测试,结果表明矩不变量的对数绝对值对旋转缩放JPEG压缩、Gaussian滤波等都具有不变性.
在Alghoniemy实验的基础上,笔者从图像库中随机选取 100幅图像做偶然攻击和恶意篡改攻击的实验.实验中先对图像进行一些修改,然后计算攻击图像导致的φ∗值的变化,结果如表 1所示.表 1中JPEG80代表对图像进行质量因子为80的JPEG压缩;剪切是指用白色像素来替代被剪切掉 32×32区域的像素;替换是指用图像一块区域替换另一块区域,或者用未知图像替换掉图像中某一区域,以达到伪造的目的.由表1可以看出,当图像被压缩或旋转缩放时φ∗的变化很小,当图像遭到恶意篡改(如剪切和替换)时φ∗的变化较大.

表1 Barbara的矩不变量φ*
可以看出,矩不变量φ∗具有半脆弱的特性,即φ∗对偶然失真具有较高的鲁棒性,同时对恶意攻击具有脆弱性.我们可利用这种半脆弱特性来区分各种攻击.
2 半脆弱水印算法
本文设计的算法由水印生成、水印嵌入、水印提取和图像认证4部分组成,水印生成和水印嵌入流程如图1,水印提取和图像认证流程如图2.
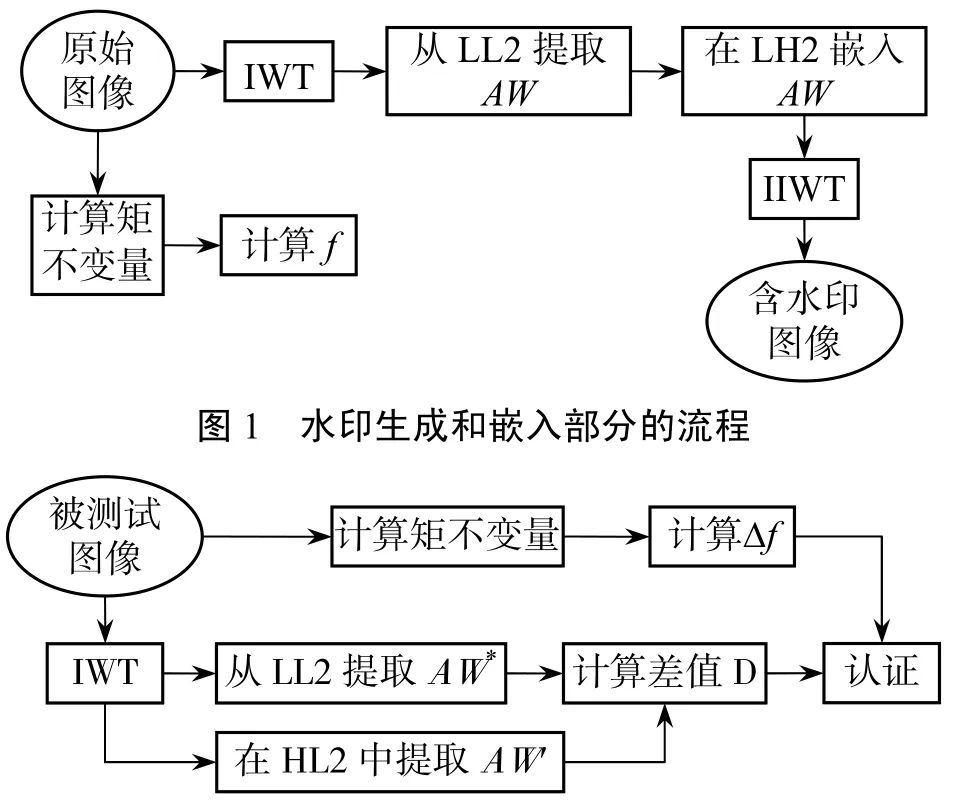
图2 水印提取和认证部分的流程
2.1 水印生成
为了满足检测和定位篡改的需要,需要生成两个水印:一个源于矩不变量,用来区分攻击;另一个源于图像特征用来定位篡改区域的水印AW.采用7个φ∗值的均值来区分攻击,即用来定位篡改区域的水印由小波变换低频子带的特征构成.对原始图像执行 2级整数小波变换(IWT)[7],小波变换的低频子带LL2包含了图像的逼近信息.对低频子带LL2的最高比特平面(MSB)按照从上到下从左到右的顺序扫描而形成的一维比特序列即为水印AW.显然,水印AW对逼近分量的变化是敏感的.
2.2 水印嵌入
水印AW应嵌入在小波域.由于JPEG压缩后图像的高频分量通常都会被去除,因此为了抵抗 JPEG压缩,可选择中频子带(如HL2或LH2)进行认证水印嵌入.为了增强算法的安全性,本文利用Arnold变换的周期性对水印进行置乱加密,经置乱后的水印信息作为最后的嵌入信息.置乱后的认证水印嵌入到HL2的第五比特平面,选择第五比特平面作为嵌入域可以同时满足水印的不可察觉性和鲁棒性.最后进行整数小波重构(IIWT)就得到了的含认证水印的图像.
2.3 水印提取
首先计算被测试图像的矩不变量的均值,记为f′(φ∗),然后对被测试图像进行2级5/3整数小波变换(IWT),从小波 LL2子带的最高比特平面提取出的信号记为AW∗.认证水印从小波分解的 HL2子带的第五比特平面提取.通过Arnold变换的对提取出的水印进行恢复,最后得到的认证水印一记为AW′.2.4 图像认证
2.4.1 图像的认证步骤
(2)计算 D(i,j)=AW′(i,j)⊕ AW∗(i,j),其中的“⊕”表示异或运算,A W′(i,j)代表AW′在位置(i,j)处的像素值,AW∗(i,j)代表AW∗在位置(i,j)处的像素值.如果在位置(i,j)处 AW′(i,j)等于 AW∗(i,j),那么差值图像的像素值为0,否则为1.差值图像中的白色像素点表示提取错误.
(3)通过实验观察可知,从恶意篡改和偶然失真中提取的差值图像是有区别的.如果图像受到偶然失真,差值图像上会呈现出一些随机分布的离散白色像素点,这是由于嵌入同步水印的过程中引入了一定的噪声.如果差值图像上有聚集的白色区域,就表明原始图像的内容在该区域受到了破坏.这样也就可以根据差值图像定位篡改位置.
2.4.2 图像D的认证水印
(1)如果Δf=0,D=0,被测试图像是真实的.
(2)如果Δf<τ,说明图像受到了偶然攻击.这种情况下,若图像受到的是几何攻击,则D表现为几乎全白的像素点;若图像受到的是其他偶然攻击,则差值信号D表现为随机分布的离散点.
(3)如果Δf≥τ,说明被测试图像的内容受到了篡改,根据差值图像D中的白色区域,可以定位出篡改区域.在这种情况下,如果差值信号D表现为几乎全黑,则说明图像受到了伪造攻击.
3 实验结果及分析
为了验证算法的有效性,从图像库中选择100幅图像进行测试.下面针对其中一幅256x256灰度图像Barbara的测试结果进行说明,见图3.

图3 256×256灰度图像Barbara的测试比较
3.1 不可察觉性分析
图3中(a)和(b)中分别是Barbara的原始图像和含水印的图像,从视觉上无法看出二者的区别,水印图像和原始图像的峰值信噪比为 42.31 dB,算法满足不可察觉性.
3.2 鲁棒性和脆弱性分析
应用Stirmark4.0对含水印图像进行了内容保持的操作,主要是不同角度旋转、不同比例缩放、广义仿射变换、不同质量因子的JPEG压缩、低通滤波等.实验结果显示对于这些操作认证系统都认为图像是真实的.另外,我们对含水印图像又作了恶意攻击,包括添加、删除、剪切和替换等操作.
根据被攻击图像的参数Δf能区分恶意篡改和偶然攻击.表2给出了认证结果,其中“Yes”表示图像受到的是偶然攻击,图像内容是真实的;“No”代表图像受到了恶意篡改.在本算法中随机选取100幅图像重复实验可以确定,阈值为0.25时具有较低的虚警率.
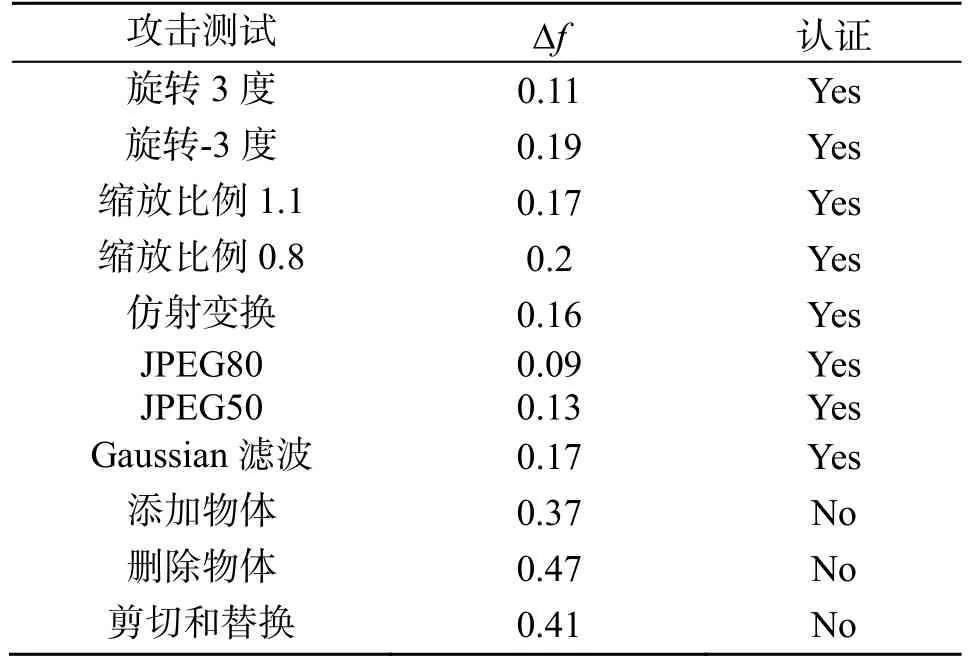
表2 Barbara图像的认证结果
图 4中((a)(b)(c)是被测试图像,(d)(e)(f)是提取水印的差值图像)给出了部分攻击后的图像:(a)是旋转3度后的图像,(b)是质量因子为75的JPEG压缩图像,(c)物体添加和删除,(d)、(e)、(f)分别给出了认证过程中对应AW的差值图像D.从实验结果可以看出,对应于JPEG压缩图像的水印差值图像其白色像素点随机分布,而对应于几何变形图像的D,几乎是全白的像素点,这是因为在水印提取之前,几何失真的图像没有经过几何校正,这样提取出来的AW∗和AW′都是有很大误差的,我们可以根据Δf判断出该图像的内容是真实的.可以看出本文的算法将几何变换和JPEG压缩都视为偶然的失真,该结论在很多应用中都是具有实际意义的.另外,实验中发现质量因子低至 40的JPEG压缩也可被认为是偶然失真.当质量因子低于40时JPEG压缩将会引起显然的视觉失真,不再适合大多数的实际应用.
对受到恶意篡改攻击的图像,从其差值图像中可以看到,对应含水印图像中的破坏区域,差值图像表现为聚集的白色区域,这样就可以准确定位篡改区域.由于用来区分攻击和定位篡改的水印都来源于原始图像,因此提高了整个系统的安全性.

图4 图像的认证和定位
本文提出了一种具有更强区分能力的半脆弱水印算法.实验结果表明,改算法不但可以检测和定位恶意篡改,同时可以抵抗一些内容保持的偶然失真,例如JPEG压缩和几何变换,特别是针对几何变换,本文的认证算法成功地解决了以往文献中半脆弱水印不能接受几何变换的问题.
[1] 张宪海,杨永田.基于脆弱水印的图像认证算法研究[J].电子学报,2007,35(1):34-39.
[2] Lin C Y,Chang S F.A Robust Image Authentication Method Distinguishing JPEG Compression from Malicious Manipulation[J].IEEE Transactions on Circuits and Systems of Video Technology,2001,11(2):153―168.
[3] Yuan H,Zhang X.Multiscale fragile watermarking based on the gaussian mixture model[J].IEEE Transactions on Image Processing,2006,15(10):3189―3200.
[4] Yu G J,Lu C S,Liao H Y M.Mean quantization blind watermarking for image authentication[J].Opt.Eng.,2001,40(7):1396―1408.
[5] Hu Ming-Kuei.Pattern recognition by moment invariant s[J].Proc.IRE,1961,49:1428.
[6] Alghoniemy M,Tewfik A H.Geometric invariance in image watermarking[J].IEEE Trans. Image Process.,2004,13(2):145―152.
[7] Daubechies 1,Sweldens W.Factoring wavelet transform into lifting step[J].Journal of Fourier Analysis,1998(4):245―267.
〔责任编辑 牛建兵〕
TP391
A
1006-5261(2010)05-0035-03
2009-10-20
河南省教育厅自然科学研究计划项目(2009C520001);黄淮学院青年骨干教师资助计划(070016)
陈萍(1969―),女,河南驻马店人,副教授.

