计量经济学模型的贝叶斯估计
——以经典单方程为例
赵 健
(1. 中南财经政法大学 统计与数学学院,湖北 武汉 430074;2. 黄淮学院 经济管理系,河南 驻马店 463000)
计量经济学模型的贝叶斯估计
——以经典单方程为例
赵 健1,2
(1. 中南财经政法大学 统计与数学学院,湖北 武汉 430074;2. 黄淮学院 经济管理系,河南 驻马店 463000)
文章以正态线性单方程为例,介绍了贝叶斯统计方法在计量经济学模型中的应用,并分析了该问题中贝叶斯估计与普通最小二乘估计的区别和联系.
贝叶斯估计;贝叶斯定理;损失函数
0 引言
贝叶斯统计是由T. R. Bayes于19世纪创立的数理统计的一个重要分支.20世纪50年代,以H. Robins为代表的学者将经验贝叶斯方法用于计量经济学模型并与经典方法相结合,此后这种方法得到了广泛应用.贝叶斯估计对经典计量经济学模型估计方法的扩展在于它不仅利用样本信息,同时也利用非样本信息.本文以正态线性单方程为例,分析贝叶斯估计方法在计量经济学模型中的应用.
贝叶斯估计是与经典估计方法相对的一种估计方法,它的基本思路是:要估计的模型参数是服从一定分布的随机变量,先根据经验给出待估参数的先验分布信息——先验信息,然后将这些先验信息与样本信息相结合,应用贝叶斯定理求出待估参数的后验分布,再应用损失函数得出后验分布的一些特征值并将其作为待估参数的估计量.贝叶斯估计与传统估计方法的不同之处在于:
1)关于参数的观点不同.经典估计方法认为待估参数θ∈Θ具有确定性;贝叶斯估计方法认为待估参数θ具有随机性,即在具体进行观测(得到样本x)之前人们根据经验对参数θ积累了一些知识,虽然θ的具体值未知,但它服从Θ上的概率分布f()θ( f()θ称为θ的先验分布).
2)利用的信息不同.经典方法只利用样本信息;贝叶斯方法要求事先提供一个参数的先验信息(一般根据专家经验提供)即非样本信息,在参数估计过程中,这些非样本信息与样本信息一起被利用.
3)对随机误差项的要求不同.经典方法中,除了最大似然法,在参数估计过程中并不要求知道随机误差项的具体分布形式,但在假设检验与区间估计时是需要的;贝叶斯方法需要知道随机误差项的具体分布形式.
4)选择参数估计量的准则不同.经典方法一般以最小二乘和最大似然为准则求参数估计量;贝叶斯方法需要构造一个损失函数(一般采用二次损失函数),并以损失函数最小化为准则求参数估计量.
1 贝叶斯统计方法
1.1 贝叶斯统计方法的理论基础
定理1 设 A1,A2,…,An,… 是一完备事件组,则对P(B)> 0的任一事件B,有

(1)式称为贝叶斯公式,其中: P(Ai)和分别称为原因的先验概率和后验概率,i=1,2,… .P(Ai)是在不知道事件B是否发生情况下诸事件发生的概率,在获得新的信息后(事件B发生后)人们对诸事件发生的概率就有了新的估计.
定理2 设θ为待估参数,θ的先验分布为g(θ),X为样本观测信息,X的密度函数记作为θ的后验分布密度函数,则有即后验信息正比于样本信息与先验信息的乘积.

例 设 X ~ N(θ,σ2),σ2已知,θ ~ N(μ,τ2)(先验分布),μ和 τ2已知,求θ的后验分布、数学期望和方差.
解:由题意知

1.2 损失函数
常用的损失函数有线性函数和二次函数,不同的损失函数得到的参数估计值是不同的.
定理3 设待估函数h(θ)的取值于R1,损失函数为L(θ,d)=λ(θ)[h (θ)−d ]2,0<λ(θ)<∞,θ∈Θ,则当λ(θ)=1时h(θ)的贝叶斯估计为
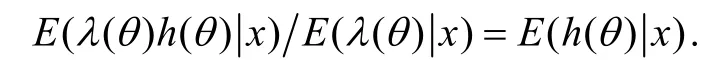
2 单方程计量经济学模型贝叶斯估计的过程
单方程计量经济学模型贝叶斯估计的过程如下:
1)确定模型的形式,指出待估参数β.
2)给出待估参数β的先验分布.β是一个多维向量,需要给出多参数的联合先验信息,若无先验信息,可取β为均匀分布.实际上常用的先验分布为自然共轭分布,即β的密度函数(先验信息)、X的密度函数(样本信息)以及两者结合后产生的函数(后验分布)服从同一分布规律.
3)利用样本信息修正先验分布,并利用贝叶斯定理导出β的后验密度函数.
4)选择二次损失函数,并利用β的后验密度函数和定理3进一步推断出β的点估计.
3 正态线性单方程计量经济学模型的贝叶斯估计
正态线性单方程计量经济学模型为
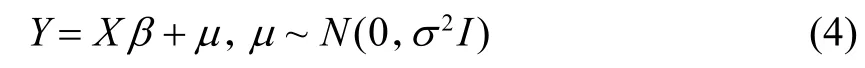
3.1 有先验信息的贝叶斯估计
这种情况下,
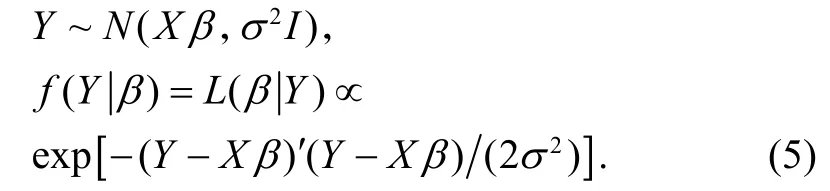
β的先验分布为自然共轭分布,即取正态密度函数
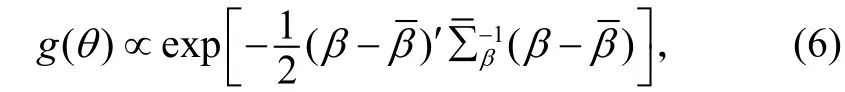
由贝叶斯定理,可得到β的后验密度函数为

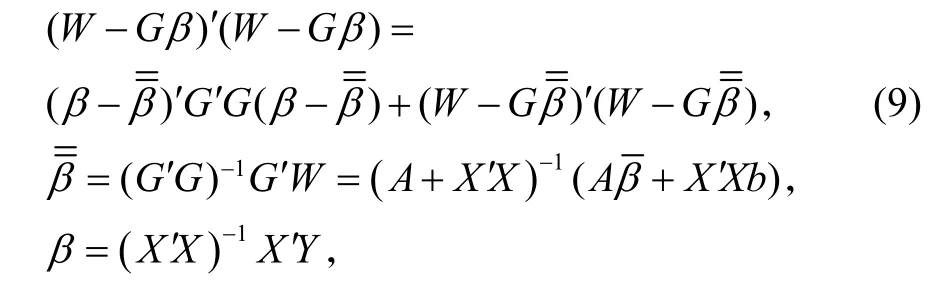
(b是β的OLS估计值),舍去(9)式右边第二项后将其代入(8)式,则有
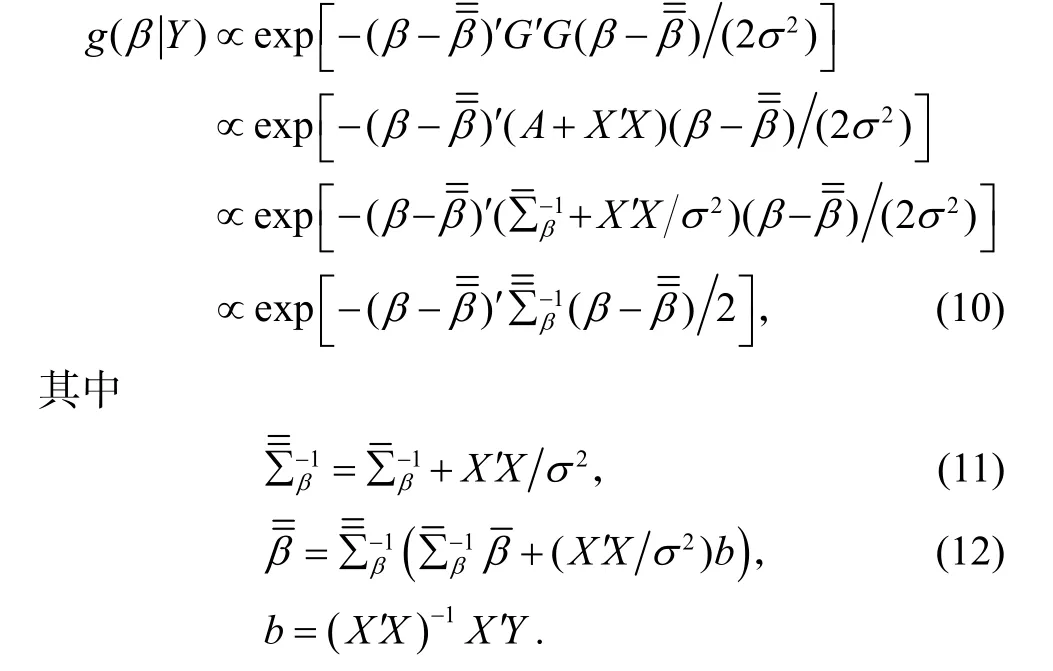

3.2 无先验信息的贝叶斯估计
在待估参数一无所知的情况下,求贝叶斯估计时,一般选取待估参数的先验分布为(− ∞,+∞)上的均匀分布,且互不相关,于是
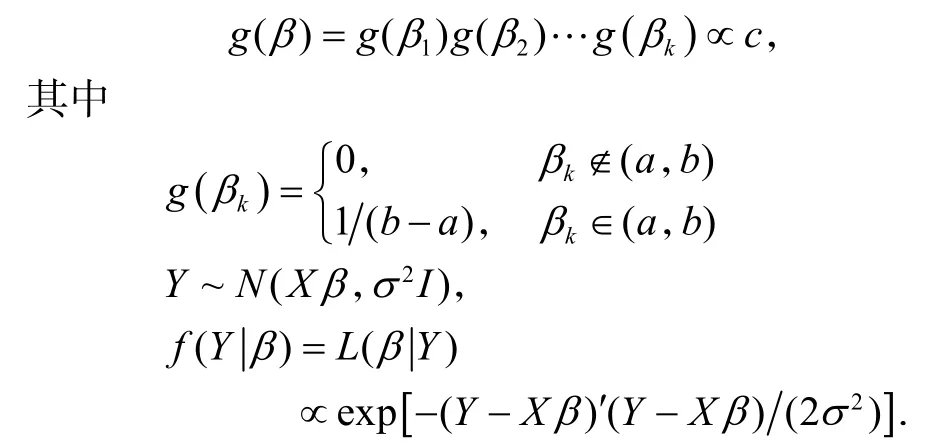

这种情况下,β的后验密度函数仍然呈正态分布,均值为 b,协方差矩阵为 σ2(X ′X)−1,即
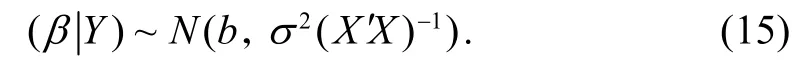
因此,β的贝叶斯估计为b,b是β的OLS估计值.可见,无信息先验得到的β的贝叶斯估计与样本信息的OLS估计相同,但是两者的含义不同.贝叶斯结论中的β是随机的,而均值b在样本确定后是固定的;样本信息的结论中,β是期望值,而b是随机变量,即有 b ~N (β,σ2(X ′X)−1).
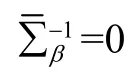

与(15)式相同.
[1] 陈希孺.数理统计引论[M].北京:科学出版社,1997.
[2] 李子奈.高等计量经济学[M].北京:清华大学出版社,2000.
[3] 李子奈.计量经济学[M].2版.北京:高等教育出版社,2000.
[4] [美]James O.Berger,Statistical decision theory and Bayesian analysis[M].Springer-Verlag,2ndEdi,1985.
[5] [美]威廉H.格林.经济计量分析[M].北京:中国社会科学出版社,2000.
〔责任编辑 张继金〕
Bayesian Estimation of Classical Econometric Linear Model
ZHAO Jian1,2
(1. Zhongnan University of Economic and Law,Wuhan Hubei 430074,China;
2. Huanghuai University,Zhumadian Henan 463000,China)
The application of Bayesian estimation methods are introduced by using normal linear single-equation econometric model as an example. The distinction between Bayesian estimation and ordinary least squares estimation (OLS)of this econometric model are analyzed.
Bayesian estimation; Bayesian theory; loss function
F224.0
A
1006-5261(2010)05-0017-03
2009-12-11
赵健(1977―),女,河南新野人,讲师,博士研究生.
——《计量经济学方法论研究》评介

