中心化子与局部中心化子探讨

陈 琳，蒋雪勤，赵占平

（1. 安顺学院 数学与计算机科学系，贵州 安顺 561000；2. 黄淮学院 数学科学系，河南 驻马店 463000）

中心化子与局部中心化子探讨

陈 琳1，蒋雪勤2，赵占平2

（1. 安顺学院 数学与计算机科学系，贵州 安顺 561000；2. 黄淮学院 数学科学系，河南 驻马店 463000）

令X是实数域或复数域F上的Banach空间，Α是X上的标准算子代数，I是Α中的单位元，设φ:Α→Α是可加映射，文章证明了如果存在正整数n，使得φ满足2φ(An+1)−φ(An)A−Aφ(An)∈FI且对任意A∈Α都成立，则存在λ∈F，使得对任意A∈Α有φ(A)=λA；文章还证明了套代数的标准子代数上的线性局部左（右）中心化子是左（右）中心化子．

中心化子；局部中心化子；标准算子代数；套代数

0 引言

设ℜ是一个环，如果对任意A，B∈ℜ，AℜB={0}蕴含A=0或B=0，则称环ℜ是素环；如果对任意A∈ℜ，AℜA={0}蕴含A=0，则称环ℜ是半素环．设映射φ: ℜ→ℜ是可加映射，若对任意A，B∈ℜ有φ(A B)=φ(A)B （ φ(A B)=Aφ(B)），则称φ是左（右）中心化子；若 φ(A2)=φ(A)A （ φ(A2)=Aφ(A)），则称φ是左（右）Jordan中心化子；若对任意A∈ℜ，存在ℜ上的一个左（右）中心化子 φA使得 φ(A)=φA(A)，则称φ是左（右）局部中心化子．Beidar证明了如果映射φ在半素环上既是左中心化子又是右中心化子，那么φ为中心化子[1]；Zalar证明了半素环上的Jordan中心化子是左（右）中心化子[2]；Vukman证明了 2-挠自由半素环上满足 2φ(A2)=Aφ (A)+ φ(A)A的可加映射是左（右）中心化子[3]；文献[4]在标准算子代数上证明了满足 φ(Am+n+1)− Amφ (A)An∈FI的可加映射φ是中心化子．按照文献[4]中的证明方法，本文将在标准算子代数上刻画满足

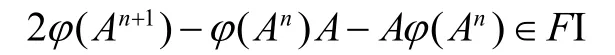
的可加映射φ的结构．

关于局部映射（局部导子，局部同构，2-局部导子）的研究已有大量成果，文献[5]研究了因子 Von-Neumann代数上范数连续的线性局部导子问题，文献[6]研究了J-子空间格代数的标准子代数上的线性局部中心化子问题．受此启发，本文研究套代数的标准子代数上的线性局部中心化子．

1 标准算子代数上的中心化子

设X代表域F上的Banach空间，L(X)表示X上所有有界线性算子的全体，F (X)代表 L(X)中所有有限秩算子构成的子空间，Α是包含单位算子和 F(X)的 L(X)的闭子代数．

引理1[7]设ℜ是一个特征不为2的素环，若φ为ℜ上的交换映射，则存在c∈C（ℜ的扩展中心）和可加映射ψ: ℜ→C，使得对任意A∈ℜ有

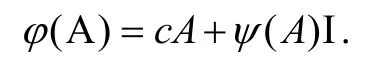
定理 1 若 φ:Α → L(X)为可加映射，如果存在正整数n，使得φ满足 2φ(An+1)− φ(An)A − Aφ (An)∈FI且对任意A∈Α成立，则存在λ∈F使得对任意A∈Α有 φ(A)=λA.

证明：1)先证明 φ(P)=Pφ (P)=φ(P)P=Pφ (P)P对任意的幂等元P∈Α成立．取幂等元P∈Α，由假设知存在λP∈F使得

(1)式两边分别左乘、右乘P，得

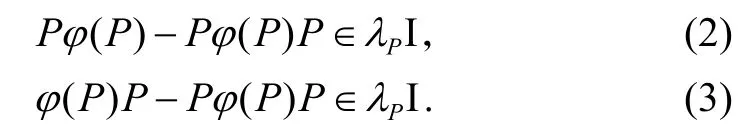
(2)式与(3)式相减得

(4)式两边分别左乘、右乘P，可得

将此式代入(2)式得 0

Pλ=，因此

2)证明存在λ∈F使得 φ(I)=λI对任意的幂等元P∈Α有 φ(P)=λP .由(5)式和φ的可加性得

即 φ(I)P=Pφ(I)对任意幂等元P∈Α都成立．因为Α包含所有的有限秩幂等算子，由P∈Α的任意性可得φ(I)=λI .在等式 φ(P)=φ(P)P中用I−P代替 P，不难得到 φ(P)=λP.

3)证明对于所有的 A∈F(X)都有 φ(A)=λA.设A∈F(X)，取幂等元 P∈F(X)使得 AP=PA=P.在假设条件中用A+P代替A得

按照每一项所含因子P的个数重新整理(6)式得

在假设条件中分别用 A + 2 P，A + 3P，…，A +nP代替A，得到以 fi(A，P)为变量的线性方程组，其系数矩阵为范德蒙矩阵

其行列式不为零，故方程组有唯一的非零解，特别地有，存在 λA，P∈FI使得

由于 Pφ (P)=φ(P)P，则(7)式两边分别左乘、右乘P可得

又由于 φ(P)=λP，于是(7)式可变为

另一方面，由(7)式和(9)式可得

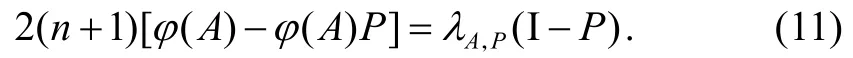
由(10)和(11)式得 φ(A)=λA+ αP + βI，其中

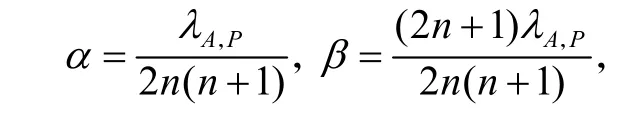
于是[φ(A)，A]=0.由于 F(X)+ FI是素的，且φ为可交换映射，由引理 1可知，存在c∈F以及可加映射ψ: F(X)+ FI → F使得对任意 A∈F(X)有

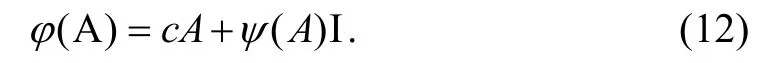
特别地，对任意一秩幂等算子x⊗f，有

由 2)可知 φ(x⊗f)=λx⊗f，因此(c − λ)x⊗f∈FI，c=λ．由于任意一秩幂零算子都可以表示成两个一秩幂等算子的差，由φ的可加性得，对任意一秩幂零算子x⊗f∈F(X)有φ(x⊗f)=λx⊗f.下面证明对所有非一秩幂零算子 x⊗f∈F(X)有φ(x⊗f)=λx⊗f.因x⊗f是非一秩幂零算子，〈 x，f〉≠0，一方面，由假设条件知存在λx⊗f∈F，使得

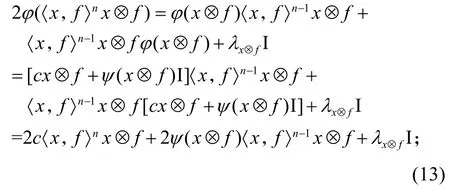
另一方面，〈x，f〉nx⊗f算子是一秩算子，由(12)式得

从而 ψ(x⊗f)=0，即 φ(x⊗f)=λx⊗f.这就证明了对任意一秩算子 x⊗f∈F(X)都有φ(x⊗f)=λx⊗f.又因为有限秩算子可表示成有限个一秩算子的和，由可加性得 φ(A)=λA.

4)证明对所有A∈Α均有 φ(A)=λA .定义映射φ1:Α→Α为 φ1(A)=φ(A)− λA，显然 φ1是可加的且满足

由3)知 φ1在 F(X)上的值为零，以下证明 φ1在Α上的值仍为零．设A∈Α且 P∈F(X)为一秩投影，令

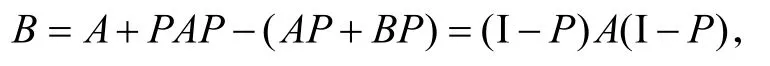
则BP=PB=0且 B − A∈F(X)，故 φ1(B)=φ1(A).由(15)式并注意到 φ1(P)=0，知存在 λB，P，∈FI使得

(16)式两边分别左乘、右乘P后再相加，可得

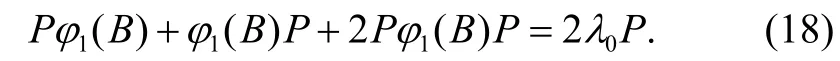
由(17)、(18)式得 Pφ1(B)+ φ1(B)P=λ0I=λ0P，故λ0=0，又由(17)式得 Pφ1(B)P=0，所以 φ1(B)=φ1(A)=0，因此对任意A∈Α有 φ(A)=λA.

定理1证毕．

2 套代数的标准子代数上的线性局部中心化子

设H代表无限维Hilbert空间，B(H)表示H上全体有界线性算子构成的集合．一个套ℕ是B(H)中一族全序正交的投影，包含0和I且在强算子拓扑下是闭的．对任意的 P∈，P−=sup{Q∈ℕ，Q＜P}，与套ℕ对应的套代数记为τ(ℕ)，其定义为Α表示包含所有有限秩算子的τ(ℕ)的一个闭子代数．

引理2[8]设一秩算子x⊗f属于套代数τ(ℕ)，则存在P∈ℕ使得 x∈P，y∈.

引理3[8]设A∈Α，若对任意的一秩算子B都有AB=0，则A=0.

定理2 套代数的标准算子代数Α上的线性局部左（右）中心化子φ是左（右）中心化子．

证明：只证左中心化子情况．对A∈Α，P 是幂等元，存在Α上的左中心化子φA，P使 φ(A P)=φA，P(A)P.对B∈Α，

φ(A P)(B −PB)=φA，P(A P(B −PB))=φA，P(0)=0，所以 φ(A P)(I − P)B=0，由引理3知 φ(A P)(I − P)=0，即 φ(A P)=φ(A P)P.对A，P⊥，存在Α上的左中心化子因为

所以 φ(A)P=φ(A P)P，进而 φ(A)P=φ(A P).对Α中任意一秩算子B=x⊗y，由引理 2知存在N∈ℕ使x∈N，y∈N.下面分两种情况讨论：

(ii)如果〈x，y〉=0，又分两种情况．若P=P−，则P+B是幂等元，因为

故 φ(A B)=φ(A)B.若P≠P−，令 x1∈P−x，x2=(P − P−)x，y1=(P − P−)y，y2=P⊥，显然 x1⊗y，x2⊗y1，x2⊗y2∈Α并且 x2⊥y1，类似于P=P−情况的讨论，可得

φ(A x1⊗y)=φ(A)x1⊗y，φ(A x2⊗y2)=φ(A)x2⊗y2；对x2⊗y1，若x2=0，则 x2⊗y1=0，显然

所以 φ(A x2⊗y1)=φ(A)x2⊗y1，再考虑φ的线性和

一秩算子B=x⊗y对任意A∈Α都有 φ(A B)=φ(A)B.对任意A，B∈Α，对Α中任意一秩算子C，则BC至多是一秩的，从而 φ(A BC)=φ(A B)C=φ(A)BC，又由引理3得 φ(A B)=φ(A)B．

定理2证毕．

[1] Beidar K，Martindal W，Mikhalev A．Rings with generalized identities[M]．NewYork：Marcel Dekker Inc，1996．

[2] Zalar B．On centralizers of semiprime rings[J]．Comment. Math. Univ. Carolinae，1991，32：609―614．

[3] Vukman J．Centralizers of semiprime rings[J]．Comment. Math. Univ. Carol.，2001，42：237―245．

[4] Qi X，Du S，Hou J．Characterization of Centralizers[J]．Acta Math. Sinica，2008，51：509―516．

[5] Zhang Jian-hua．Local derivation of nest subalgebras of Von Neumann algebras[J]．Linear Algebra Appl.，2004，392：61―69．

[6] Wei Qiong，Li Peng-tong．Centralizers of J-subspace lattice algebrs[J]．Linear Algebra Appl.，2007，426：428―437．

[7] Bresar M．Centralizing mappings and derivation in prime rings[J]．J. Algebra,1993，156：385―394．

[8] Davidson K．Nest algebras[M]．Pitman Research Notes in Mathematics Series. 191,Longmans Scientific and Technical，1988．

〔责任编辑 张继金〕

Centralizers and Local Centralizers

CHEN Lin1,JIANG Xue-qin2,ZHAO Zhan-ping2
(1. Anshun College,Anshun Guizhuo 561000,China; 2. Huanghuai University,Zhumadian Henan 463000,China)

Let X be a Banach spaces over the real or complex field F. Let Α be standard operator algebra on X with unit I. In the first part,suppose that φ:Α→Α is an additive map and n is a positive integer,it is proved that,if φ satisfies 2φ(An+1)−φ(An)A−Aφ(An)∈FI for all A∈Α,then there exist some λ∈F such that φ(A)=λA. In the second part,it is proved that every linear local left (right)centralizer of standard subagebra of nest algebra is a left (right)centralizer.

centralizer; local centralizer; standard algebra; nest algebra

O177.1

A

1006-5261(2010)05-0001-03

2010-03-17

陈琳（1981―），男，河南驻马店人，讲师，硕士研究生．