L’ Hospital法则的应用及其常见问题
陈 敏
(黄淮学院 数学科学系,河南 驻马店 463000)
L’ Hospital法则的应用及其常见问题
陈 敏
(黄淮学院 数学科学系,河南 驻马店 463000)
介绍了L’ Hospital法则在未定式极限求解方面的应用,讨论了L’ Hospital法则的应用中易出现的问题并给出了相应的解决方法.在用L’ Hospital法则求极限时,必须对L’ Hospital法则成立的条件进行验证,否则可能得到错误的结果.
L’ Hospital法则;未定式;极限
L’ Hospital法则是求解未定式极限的重要方法,它可以求解的未定式极限的主要类型有0/0,∞/∞,0·∞,∞−∞,1∞,∞0和00型.由于表示这些极限的函数或变量形式多样,变化无穷,在运用L’ Hospital法则时,必须注意是否符合法则成立的条件,否则可能导致运算的繁琐甚至得到错误结果.
1 L’ Hospital法则

2 0/0型和∞/∞型极限的求解
例1 求下列极限[1―2]:
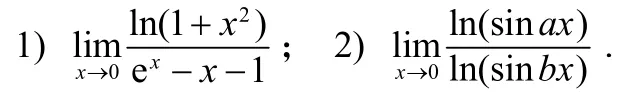
解:1)该极限属于0/0型未定式,可直接用L’ Hospital法则求解.
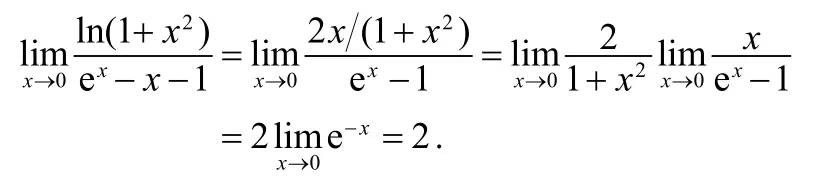
2)该极限属于∞/∞型未定式,也可以直接用L’ Hospital法则求解.
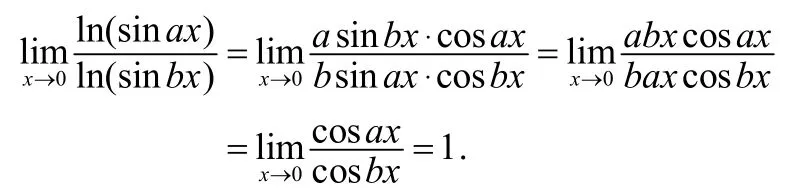
由例1可知,对于符合L’ Hospital法则要求的0/0型及∞/∞型未定式,可结合极限的运算法则及等价无穷小代换等方法,使运算过程得到简化.
3 0·∞型和∞−∞型极限的求解
对于0·∞型及∞−∞型未定式极限,一般首先作代数恒等变形,将其化为 0/0型或∞/∞型未定式极限,然后应用 L’Hospital法则求解.
例2 求下列极限[3]:
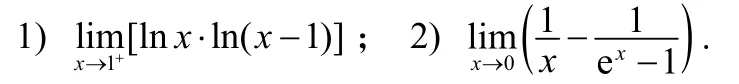
解:1)该极限属于0·∞型,可以化为0/0或∞/∞型.
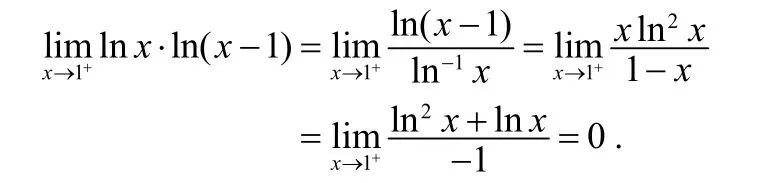
2)该极限是∞−∞型未定式,对极限表达式的两分式通分后可化为0/0型未定式.
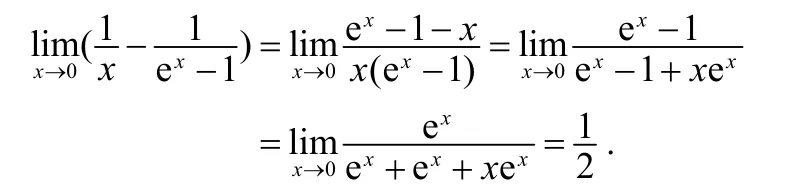
4 1∞型、∞0型和00型极限的求解
对于1∞型、∞0型和00型未定式极限,一般可先用对数的性质、代数恒等变形等方法把极限表达式的幂指数函数化为lim uv=exp(limv lnu)的初等函数形式,再对limv lnu恒等变形后应用L’ Hospital法则求解.
例3 求下列极限[2―3]:

由例3可知,在应用L’ Hospital法则求幂指函数的极限时,用代数替换等方法可简化计算.
5 L’ Hospital法则的应用中应注意的问题
应用L’ Hospital法则求极限时,应注意以下问题:
(1)只有未定式极限,才能用L’ Hospital法则求解,否则会得到错误的结果.
(2)由于L’ Hospital法则的条件是充分而非必要的,因此limu′/v′不存在并不说明limu/v也不存在,可运用其他方法求解.
(3)若分子、分母多次求导后极限表达式出现循环,并不代表极限不存在,可通过恒等变形等方法求解.
(4)在应用L’ Hospital法则时,可综合应用恒等变形、变量代换、因式分解、等价无穷小替换等方法,从而简化求解过程.
(5)对于一些多元函数的极限,可以通过变量代换将其变换为一元函数的极限函数,然后用L’ Hospital法则求解.

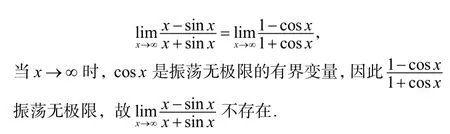
分析:原极限是存在的,但不适合用L’ Hospital法则求解.此问题可用无穷小性质求解.
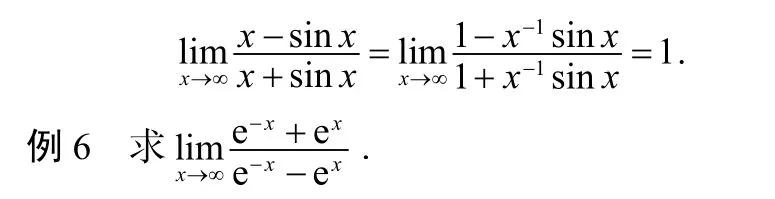
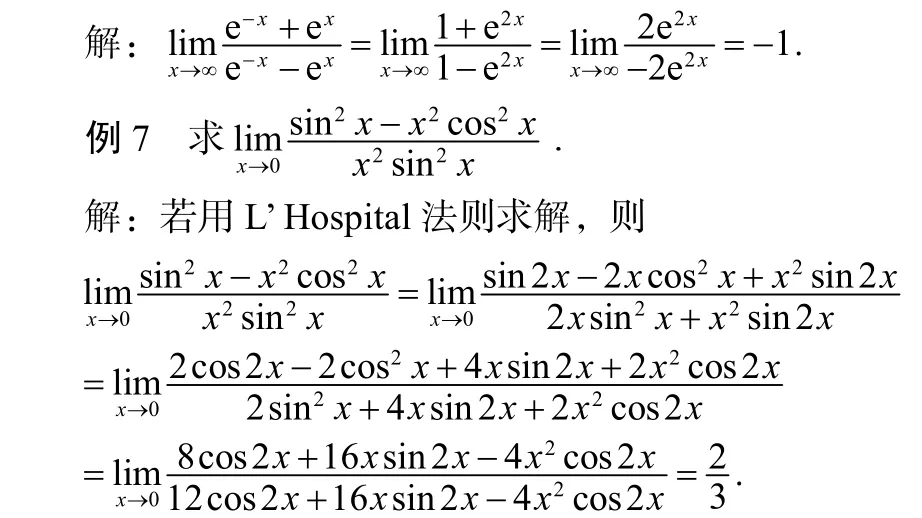
这种解法较为繁琐,稍不注意就会出现错误.
例7的另一种解法如下:
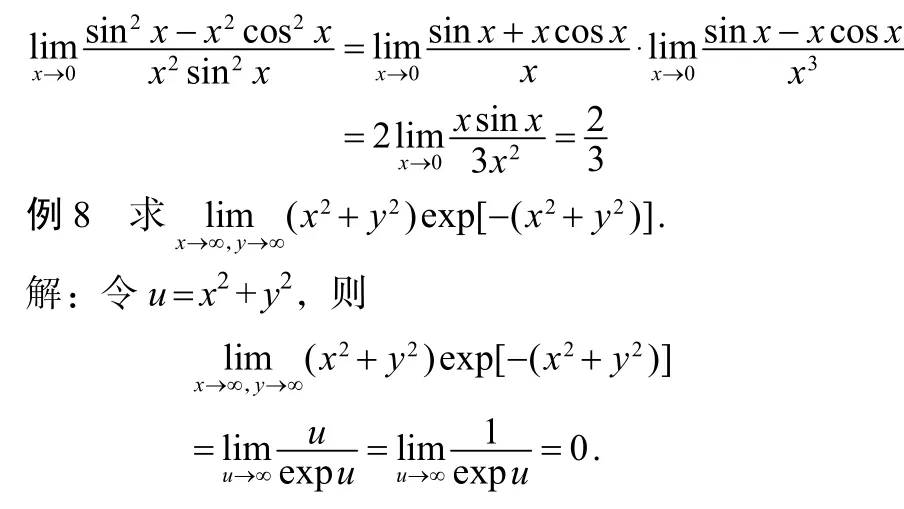
综上所述,在用 L’ Hospital法则求极限时,必须对 L’Hospital法则成立的条件进行验证,否则可能得到错误的结果.另外,对所求极限表达式的形式进行灵活变换,根据极限表达式的特点将L’ Hospital法则与其他方法相结合,可以简化极限的求解.
[1] 周誓达.微积分(经济类与管理类)[M].北京:中国人民大学出版社,2005.
[2] 费定晖.吉米多维奇数学分析习题集题解[M].济南:山东科学技术出版社,2003.
[3] 傅英定,谢云荪.微积分:上册[M].北京:高等教育出版社,2003.
〔责任编辑 张继金〕
O171
A
1006-5261(2010)05-0028-02
2009-11-18
陈敏(1982―),女,河南正阳人,助教.

