一种新的变步长 LMS自适应滤波算法

杨红, 李德敏, 林苍松, 杨旭

(①东华大学信息科学与技术学院,上海 201620;②中国电子科技集团公司第五十研究所,上海 200063)

0 引言

自适应滤波是现代信号处理技术的重要研究领域。几十年来,众多的学者对LMS算法[1-9]的性能分析和算法改进方面进行了大量的研究工作,在理论上和应用上都积累了丰富的经验,并且提出了许多 LMS算法的改进算法,文献[3-4]提出了一种自适应步长随迭代次数n的增加而逐渐减小的变步长算法,该算法对非时变系统稳态误差非常小,但不具有对时变系统的跟踪能力。文献[5]提出的变步长算法中,其步长因子与 e(n)和 x(n)(滤波器 n时刻输入矢量)的互相关函数的估值成正比,在干扰加大的情况下,该算法仍具有良好的性能,但计算量大不易实时实现。文献[6]通过对误差信号e(n)进行非线性处理,得到了一种变步长算法,该算法计算量适中,稳态失调小,但收敛速度不够快。文献[7]提出了一种步长因子与误差信号 e(n)之间满足非线性函数关系的滤波算法,该算法对非相关信号有较高的处理性能,但对于强相关信号算法性能急剧下降。文献[8]用误差信号e(n)的自相关时间均值来调整步长,但收敛效果不太明显。文献[9]提出了一种解相关算法,该算法具有很好地处理强相关信号的能力,但收敛速度有待进一步提高。

[7]建立步长因子与误差信号 之间的非线性函数关系,并借鉴文献[9]归一化的思想,将两种算法有机结合,提出引入输入信号因子,得到了改进的 LMS算法,该算法不仅获得了较快的收敛速度,较好的跟踪性能,还能在输入发生突变的情况下保持较小的稳态误差。

1 算法分析

1.1 改进的 SVSLMS算法

滤波器的原理框图如图1。

图 1 自适应滤波原理框

其误差信号为：

W(n)的迭代公式为：

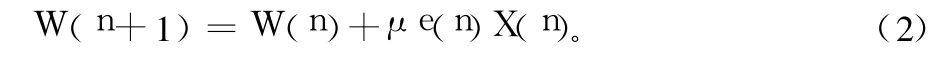
文献[7]中的步长：

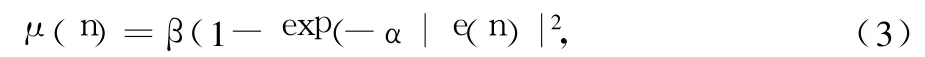
式中,e(n)为误差信号,X(n)为 n时刻输入信号矢量,W(n)为n时刻N阶自适应滤波器的权系数,α控制步长的形状,β控制步长的大小,μ是步长因子,收敛的条件是 0＜μ＜1/2λmax,λmax是输入信号自相关矩阵的最大特征值。

1.2 归一化的 NLMS算法

固定步长的自适应滤波算法 NLMS[10](归一化 LMS)采用如下算式调整自适应滤波器参数：

其中,μ为归一化调整步长,A(n)为n时刻自适应滤波器的系数矢量：

其中 N为自适应滤波器的阶数。

1.3 变步长 N-SVSLMS算法分析

文献[7]提出的算法运算简单,在稳态阶段步长很小且变化不大,在自适应均衡中也能取得较好的效果。但此算法易受到信号输入端不相关噪声的干扰,影响了算法的稳定性。新算法的引入分析为：定义输入矢量X(n)在 n和n-1时刻的相关系数为：

从矢量 X(n)中去除与X(n-1)相关的信息量,并定义为新矢量：

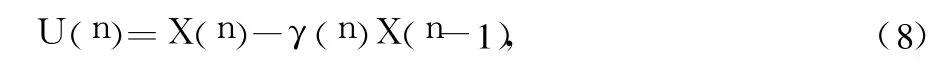
由式(7)和式(8)得：

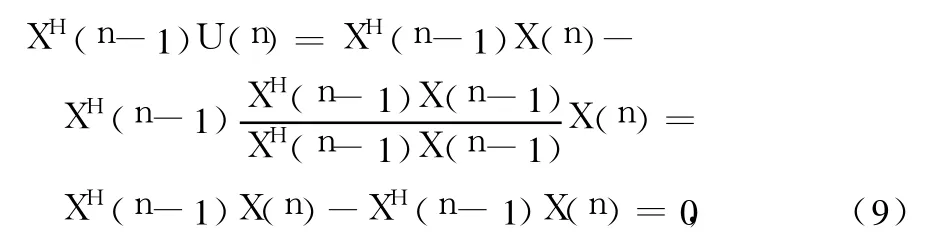
式(9)表明 U(n)与 n-1时刻的信号 X(n-1)正交,这种正交性加快了算法的收敛速度。由于矢量U(n)表示信号矢量X(n)中和以前时刻分量无关的部分,因此定义当前信号的有效能量为：

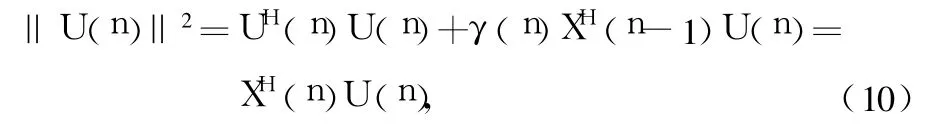
故‖U(n)‖2又称为归一化能量因子,将矢量 U(n)看作为滤波器n时刻的输入,可得权系数更新公式为

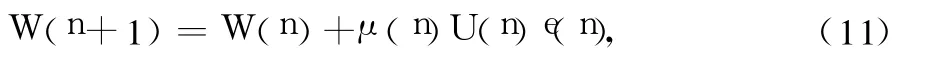
文献[7]中的算法是一种步长因子与误差信号 e(n)之间满足非线性函数关系的滤波算法,该算法对非相关信号有较高的处理性能,但在高信噪比下收敛不够快;文献[9]中的解相关算法具有很好地处理强相关信号的能力,但在信道突变的环境下不够稳定;结合文献[7]和文献[9]两种算法的优点,在此基础上,通过引入输入信号因子U(n),建立归一化的思想和步长因子μ与误差信号之间的非线性函数关系,使之能根据滤波器的输入信号能量和实时误差改变步长,加快收敛速度。

这里算法的步长计算公式为：

其中,μ1(n)β(1-exp(-α|e(n)|2)已在文献[7]中给出,U(n)为输入信号因子,δ是一个小的正数,它保证分母不为零,且 0＜δ≪‖U(n)‖2,μ满足：

将式(12)代入到式(11)中,得到新算法权系数更新公式为：

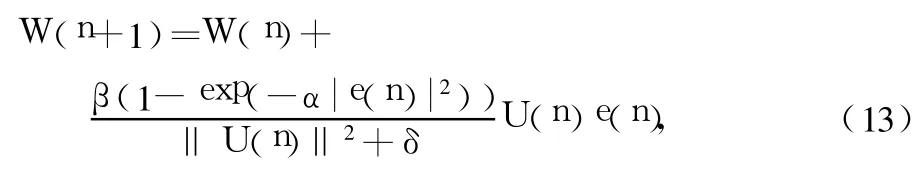
其中,δ是一个小的正数,它保证分母不为零,且 0＜δ≪‖U(n)‖2,收敛因子 μ满足或 0＜μ＜2。其中α控制步长的形状,β控制步长的大小。在保证较小的稳态误差条件下,改进的算法保证了较快的收敛速度和较好的跟踪性能,并且当输入信号发生变化时,能很好的跟踪并获得较小的稳态误差。所以,改进算法具有较好的抗干扰性能,且其收敛性和稳态误差等也明显改善。不仅保持了原算法的优点,而且在低信噪比环境下,性能更加优良,应用范围也更加广泛。

2 性能仿真及分析

2.1 时域波形分析

从图 2中可以看出信号 s经过未知信道后,波形发生了明显的变化,而经过自适应滤波后,波形的到了恢复,且在10～20个比特时达到收敛。信号因噪声的影响而上下波动,自适应滤波克服了这一缺点。从图 2的比较可以看出,该算法具有更好的处理结果,对自相关较弱的噪声不再敏感,有较强的鲁棒性,体现了自适应滤波的特点。

图 2 信号的时域波形

2.2 收敛性能分析

下面通过计算机仿真来给出改进的变步长 N-SVSLMS自适应滤波算法和已有算法的性能比较,采用以下计算机仿真条件：

①自适应滤波器阶数L=4;

②未知系统系数矢量 h1=[0.8.0.6]T,h2=[0.9,0.3,0.2]T,h3=[1,0.7,0.5,0.25]T;

③参考输入信号 x(n)为贝努利二进制随机序列;

④噪声信号 v(n)是与 x(n)不相关的高斯白噪声,其均值为零,方差为 1。分别做 1 000次独立的仿真,采样点数为200,然后求其统计平均,采用对数坐标得出 e(n)的收敛曲线,该算法初始系数均为 0,标准 LMS算法的步长 μ=0.01;改进的SVSLMS算α=20,β=0.05(这里本实验最佳取值);NLMS算法 μ=1;算法 α=20,β=0.5(该实验最佳取值)。

图 3为在矢量 h1环境下的仿真曲线,图 4为在矢量 h2和 h3环境下的仿真曲线。

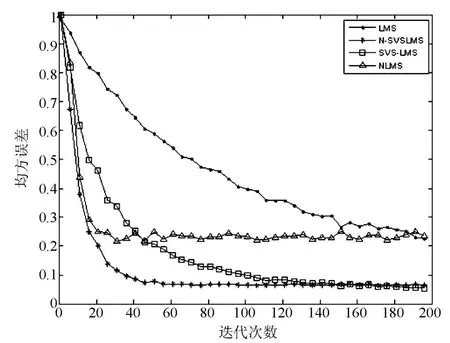
图 3 两径信道下四种不同算法的收敛曲线

由图 3可以看出,在相同的稳态误差情况下,本文算法的收敛速度明显快于其他算法,改进的 SVSLMS算法[7]要快于标准 LMS算法,归一化算法(NLMS)[11]收敛速度很快,但不够稳定,这里算法(N-SVSLMS)比上述三种算法收敛速度要快,而且更趋于稳定。在达到相同均方误差的情况下,NSVSLMS算法的收敛速度明显快于标准 LMS算法和改进的SVSLMS算法,稳定性要优于 NLMS算法。

图 4左右两边的敛收曲线分别是在h2和 h3环境下的曲线图,由图 4可以看出,在良好的信道环境下,NLMS收敛速度很快,但在信道环境突变的情况下,NLMS不但没有收敛,并且还出现了严重的失真,通过比较得知,N-SVSLMS的稳定性要优于其他算法,并适用于多种信道。

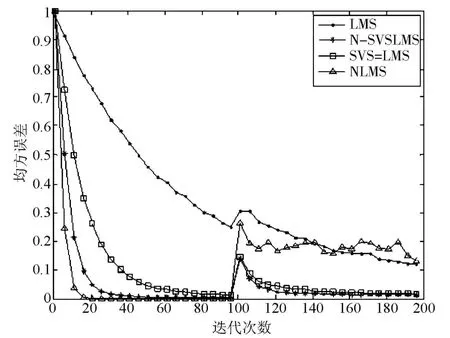
图 4 多径信道下四种不同算法的收敛曲线

在四种算法保持同样的收敛速度时,N-SVSLMS算法具有较小的稳态失调量,性能明显优于其他算法,该算法在启动初期有较大的收敛步长,使算法有较快的收敛速度;在算法深度收敛时有一个较小的步长,使得算法可以获得较小的稳态误差,较好地解决了收敛速度和稳态误差的矛盾。而且该算法对不相关噪声还具有较强的抗跃变能力和鲁棒性。此算法性能明显改善,这也符合变步长自适应算法的思想。

3 结语

通过建立步长因子与误差信号之间的合理非线性函数关系,提出一种归一化的变步长 LMS自适应算法。该算法具有初始阶段和系统时变阶段步长迅速增大而稳态阶段步长自适应减小,并且不容易受噪声干扰的特点。理论分析和计算机仿真结果表明该算法具有收敛速度好、跟踪速度快,收敛精度高的特点,理论分析和实验结果表明该算法明显优于现有算法。

参考文献

[1]孙静,陶智,顾济华,等.基于 LMS自适应滤波的耳语音增强的研究[J].通信技术,2007,40(12)：394-396.

[2]任晓亚,宋爱民.自适应算法在干扰抵消器应用中的比较研究[J].通信技术,2007,40(12)：48-50.

[3]GITLIN R,WEINSTEIN S.The Effects of Large Interference on the Track-ing Capability of Digitally Implemented Echo Cancellers[J].IEEETrans on Com,1978(06)：833-839.

[4]DARKEN C,MOODY J E.Towards Faster Stochastic Gradient Search[C]∥MOODY J E,HANSON S J,LIPPMANN R P.Advances in Neural Information ProcessingSystems4.SanMateo：Morgan Kaufmann,1992：1009-1016.

[5]叶华,吴伯修.变步长自适应滤波算法的研究[J].电子报,1990,18(04)：63-69.

[6]吴光弼,祝琳瑜.一种变步长 LMS自适应滤波算法[J].电子学报,1994,22(01)：55-60.

[7]高鹰,谢胜利.一种变步长 LMS自适应滤波算法及分析[J].电子学报,2001,29(08)：1094-1097.

[8]李方伟,张浩.一种新的变步长 LMS自适应滤波算法及其仿真[J].重庆邮电大学学报：自然科学版,2009,21(05)：591-594.

[9]王振力,张雄伟,杨吉斌,等.一种新的快速自适应滤波算法的研究[J].通信学报,2005,26(11)：1-6.

[10]HAYKINETS.Adaptive Filtering Theory[M].USA：PrenticHall,1985.

[11]DINIZ PS R.Adaptive Filtering：Algorithms and Practical Implementation,Secend Edition[M].USA：Spring,2002.