基于 T-S模糊模型的非线性系统状态估计

张永锋

(四川大学数学学院,四川 成都 610064)

0 引言

在目标跟踪或动力系统领域中,非线性系统的状态估计越来越得到人们的青眛。中将数据融合方法运用于机器人系统设计中[1],使用传统的方法处理了估计及滤波设计问题[2-3],文献[4]中也使用了最小二乘的方法,但主要思想是基于泰勒展式对非线性系统的线性化,如扩展卡尔曼滤波(EKF)[5-6],但对高度非线性的系统,用(EKF)的效果不是十分好,还有一些使用统计技术的方法,如文献[7]中通过选取样本粒子去离散化非线性系统,然后基于选取的粒子去滤波,如无味滤波,粒子滤波等,遗憾的是这些方法的计算复杂度非常大,不适于实时的目标跟踪。最近几十年来,有控制系统领域的学者提出用模糊推理方法对非线性系统建模逼近去找状态估计[8],其中最著名的有 T.Takagi和 M.Sugeno提出的模糊规则逼近模型(T-S模型)。

将模糊推理理论与Kalman滤波结合,提出一种对非线性系统目标状态估计的新方法。这个方法的主要思想是：①用局部状态空间模型族表示一个模糊系统;②对每个局部状态系统滤波得到局部状态估计;③从这对 m个局部状态估计进行模糊线性组合,并进行加权优化处理得到全局估计。能够证明这样构造的全局状态估计是一个无偏的,且稳定的。在给出的货车 -拖车仿真实验中,用此方法与一般的EKF方法进行了比较,验证了用T-S模型规则推理方法得到的估计值的有效性,并给出一些分析的结果。

1 问题阐述

一个非线性函数可以用一族线性函数去逼近,同样,对任意一个非线性系统可以用下面的 m个模糊规则表示的线性系统去逼近它。

其中：

因为zk是xk或uk的非线性函数,用上式表示的系统是时变的非线性系统,为了对每个局部的线性时不变系统进行状态估计,可以构造出每个局部系统的状态 xi(k)与输出yi(k)如下：

定理 1 由式(3)定义的状态xi(k)与 yi(k)的状态方程可用下面的系统来表示：

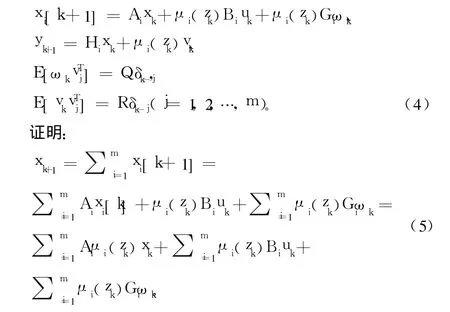
把式(3)定义的矩阵代入式(5)得到：

式(6)是式(1)描述的全局系统的状态模型,因此式(4)式描述的是状态xk的动态行为。用同样的方法可以证明观测方程的情形。

2 模糊系统卡尔曼滤波

卡尔曼滤波的理论的发展已经很成熟了,下面给出经过修正的模糊线性系统的模糊卡尔曼滤波公式。模糊卡尔曼滤波方程与标准卡尔曼滤波方程不同的是式(4)表示的是个模糊的系统,经过下面的滤波公式,得到局部的目标状态估计 ,利用这个局部的估计得到一个所表示的全局模型系统的状态估计每个时间步,模糊卡尔曼滤波为：

有了 m个局部估计 x1[k],x2[k],…,xn[k],就可得到一个无偏估计 xˆk|k=Pk|kXk其中 ：

因为对于一个非线性系统用T-S模糊规则的方法得到了一个全局的状态估计为：xˆk|k=Pk|kXk是对 x的线性无偏估计中,这是因为每个局部的估计是线性无偏的,全局估计是它们的一个加权和形式,根据矩阵论的理论,如此构造的全局估计仍具有无偏性,在后面的仿真实验中,可以看到在解决高度非线性问题是时,EKF的性能并不是十分好,但用现提出的基于T-S模型的规则推理得到的估计可以表现出良好的性能,因此用现提出的方法处理非线性系统具有一定的实际可行性.

3 仿真与计算

在文献[9]中考虑寻求非线性系统最优控制时提出了下面表述的货车-拖车系统,由于此系统涉及到货车与拖车的角度信息,所以具有高度的非线性,用EKF方法去估计系统的角度信息表现出的性能不是很好,下面用这里提出的基于T-S模糊模型的方法处理该系统的状态估计问题,并将于EKF方法进行比较

其中,x0(k)是货车的方向角,x2(k)是拖车方向角,x3(k)是拖车尾部纵向位置,x4(k)是拖车尾部水平位置,uk是转向角.l是货车的长度,L是拖车的长度,T是采样时间,v是恒定的倒退速度,在仿真实验中取L=5.5m,t=0.05 s,l=2.8 m,v=-1.0m/s。对于式(8)描述的非线性系统,利用 T-S模糊规则理论,可以将它用下面的可加噪声的模型来表示：

图 1EKF方法货车方向角误差

图 2 T-S方法货车方向角误差

4 结语

本文利用可加性噪声的T-S模糊规则对非线性系统给出了一个状态估计,是无偏的并且在线性最小误差方差意义下最优估计,仿真的结果表明用基于 T-S的模糊规则与EKF结合的方法对非线性系统进行状态估计能取的良好的效果,并且能表现出很好的稳健性。

[1]赵海,王光兴,数据融合论在机器人系统设计中的应用[J].[EB/OL].(2010-03-01)[1995-03-01].http：//www.cnki.com.

[2]徐自励,华伟,王一扬.多窗谱估计法估计相干函数的双端语音检测[J].通信技术,2007,40(05)：75-76.

[3]安勇,牟容增,陈家国,等.基于多级内插的基带信号成形滤波设计[J].通信技术,2008,41(05)：4-6.

[4]崔健陈洪 张尔扬 .一种 MC-CDMA最小二乘信道估计的改进算法[J].通信技术,2008,41(07)：112-114.

[5]BOZIC S.Digital,Kalman Filtering[M].USA：Halsted Press,1994.

[6]TAKAGI T,SUGENOM.Fuzzy Identification of Systems and Its Applications to Modeling Andcontrol[J].IEEETrans Syst.Man Cybernetics SMC,1985,15(01)：116-132.

[7]PARIZ N.A Robust Fuzzy Model Following Observer‐Based Control Design for Nonlinear System[J].USA：IEEE,2006：5040-5043.

[8]CHEN G,WANG J,SHIEH L.Interval Kalman filter[J].IEEE Trans.Aerosp.Electron.Syst,1997(33)：250-259.

[9]CHEN G,XIE Q,SHIEH L.Fuzzy Kalman filtering[J].Inf.sci,1998(109)：197-209.