流水线 CORDIC算法的 FPGA实现

王亚春, 蔡德林, 张梦龙, 王俊

(①安徽大学电子科学与技术学院,安徽 合肥 230039;②中国电子科技集团第 38研究所,安徽 合肥 200031)

0 引言

坐标旋转计算机(CORDIC,Coordinate Rotational Digital Computer)算法是 Volder于 1959年在美国航空控制系统的设计中提出来的,它是一种用于计算运算函数的循环迭代算法。其基本思想是用一系列与运算基数相关的角度的不断偏摆,从而逼近所需旋转的角度,从广义上讲它是一个数值计算逼近的方法。这些固定的角度与计算基数有关,运算只有移位和加减,可通过该算法不同的实现模式(如圆周模式、双曲线模式、线性模式等)来计算的函数包括乘、除、平方根、正余弦、反正切以及指数运算等。1971年,J.S Walther提出了统一的CORDIC算法形式,把圆周旋转、双曲旋转和直线旋转统一到同一个CORDIC迭代方程中,为同一硬件实现多功能运算奠定了基础。在传统的硬件算法设计中,乘、除等基本数学函数运算是一种既耗时又占用面积大的运算,CORDIC算法正是为解决这种问题而产生的,它从算法本身入手,将复杂的算法分解成一些在硬件中容易实现的基本运算,如加法、移位等,从而使得这些算法在硬件上可以得到较好的实现。

1 CORDIC算法的基本原理

以基于圆周模式的 CORDIC算法实现为例,介绍CORDIC算法的基本原理[1]。假设平面直角坐标系里有一向量：a(xi,yi)=a(r cosα,r sinα),现将其旋转 θ角得到新向量：b(xj,yj)=b(r cos(α+θ),r sin(α+θ)),如图 1所示,则有：

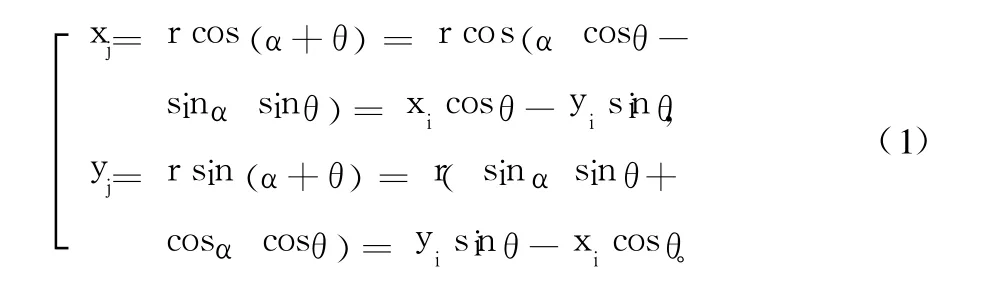
图 1 CORDIC算法旋转示意

写成矩阵形式就是：

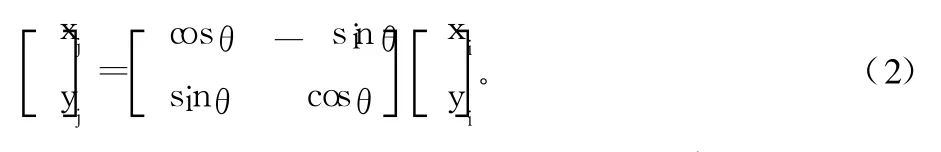
如果向量 a(xi,yi)经过 n次旋转才到达 b(xi,yi),其中第 k次旋转的角度为 θk,那么第 k次旋转的表达式为：

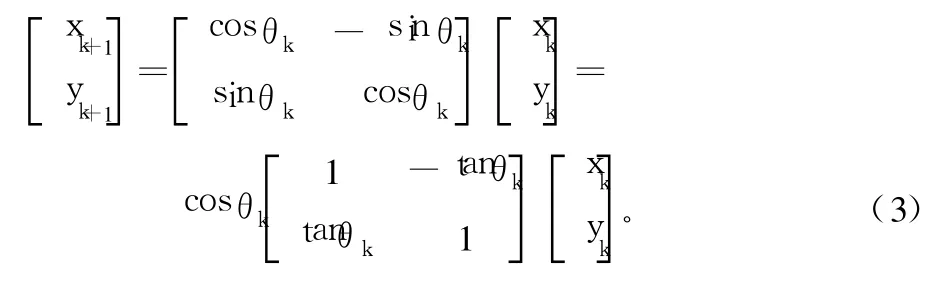
如果限制 tanθk=±2-k,则可以将 tanθk乘项的乘法操作变为移位操作,式(3)将只有一个乘积项 cosθk：

θk=Skarctan 2-k,Sk={-1,+1}。

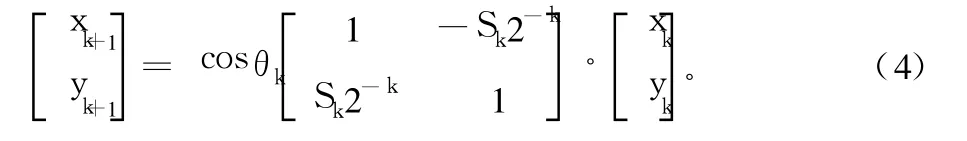
除了 cosθk系数外,CORDIC算法只需要简单的移位和相加操作即可完成。事实上 cosθk还可以事先算出来。考虑到：

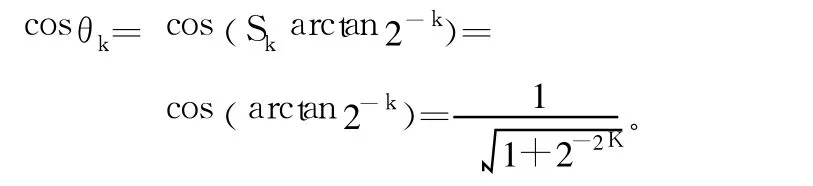
经过无数次迭代后,cosθk系数项将变成一个常数。由于 cosθk系数项是一个常数,因此可以在迭代的过程中忽略cosθk系数项,迭代的最后再将其乘入。这样迭代式就变为：

式(5)就是 CORDIC算法的迭代式。假设 z代表的是尚未旋转的角度：

zk+1=(总角度 -已旋转角度)=zk-Skarctan 2-k(未旋转角度-刚旋转角度),将此式和式(5)结合就得到了下面三个迭代方程式：其中 Sk的符号由第 k次旋转时候的角度 zk决定,它们的关系是：Sk=-1,zk＜0

+1,zk≥0,向量 a(xi,yi)向向量 b(xj,yi)逼近的精度由迭代的次数决定,迭代的次数越多,逼近的精度就越高,迭代 n次(n→∞ )得到的最终结果为：

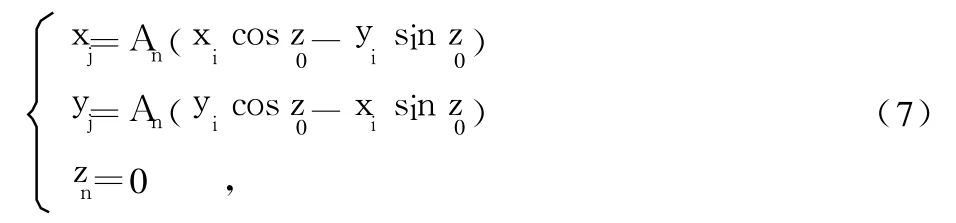
其中zn=0表明旋转到了指定的角度。

2 CORDIC流水线结构的 FPGA实现

CORDIC流水线结构的 FPGA实现参考文献[2-4]。在实际应用中,CORDIC的实现方式应该根据目标需求,在速度和资源之间进行折中。采用流水线结构,这种方式能够在执行进程的同时输入数据,从而极大提高了程序的运行效率,在该结构中,每一个移位器都是固定的深度,而且旋转角度集的各个值作为常数直接连接到累加器上,不需要存储空间和读取时间,图 2是CORDIC算法的一般流水线结构。

图 2 CORDIC算法的一般流水线结构

3 仿真结果与分析

仿真结果与分析参考文献[5]。该设计中选用的FPGA芯片是 Altera公司 CycloneⅢ系列中EP3C25F256C6器件,使用 VHDL语言完成电路描述之后,在QuartusⅡ软件平台上进行编译、仿真的结果如图 3所示(表 1列出其计算结果)。

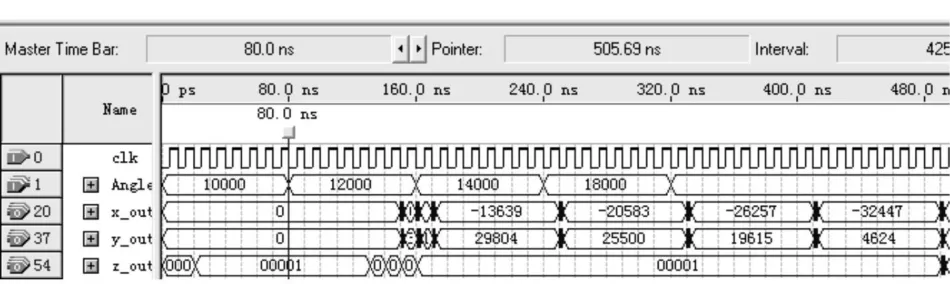
图 3 用FPGA实现CORDIC算法的时序仿真

其中输入信号有两个,分别为时钟 clk和要计算的角度Angle。输出则有 3个,分别是 x_out(余弦值)、y_out(正弦值)和 z_out(迭代结束时的角度误差)。由式(7)可知,为了使最后结果中 x_out和 y_out分别为余弦值和正弦值,就应该设置 xi和 yi的初始值分别为 1/An和 0。但程序里的初始值并不是这样设置的,这是因为把第一次迭代精简在了初始值中设置,同时还进行了预处理,即扩大了输入角度的范围。图 3仿真结果中,输入角度Angle用十六进制数表示,计算出的正弦值y_out和余弦值 x_out则用带符号整数表示。 无论是输入角度 Angle还是输出的正、余弦值均扩大了 215倍,实际的角度和计算结果应该除以 215。表 1列出了图 3的仿真结果中的 4个角度和CORDIC计算结果,同时还列出了理论的正弦值和余弦值。可以看出,经过 16次迭代后,CORDIC计算结果已经非常精确。

表 1 CORDIC计算结果与理论值的比较

4 结语

探讨了 CORDIC算法的一种硬件实现,它具有速度快、精度高、结构简单易实现等优点,从实验结果来看,其误差很小,能够满足速度和精度的要求,因而具有十分重要的工程研究和应用意义。

[1]VOLDER JE.The CORDIC Trigonometric Computing Technique[J].IRE Trans.Electronic Computers,1959(EC-8)：330-334.

[2]徐光辉,程旭东,黄如,等.基于 FPGA的嵌入式开发与应用[M].北京：电子工业出版社,2006.

[3]田耘,徐文波,张延伟,等.无线通信 FPGA设计[M].北京：电子工业出版社,2007.

[4]UWE M B.数字信号处理的 FPGA实现[M].北京：清华大学出版社,2006.

[5]徐小峰,唐治德,邓玉娟,等.基于 CORDIC算法的 QAM调制器的 FPGA实现[J].通信技术,2008,41(09)：9-11.