工资 薪金所得个人所得税相关命题的证明与运用

陈诗谷

一、命题的提出

在实际工作中人们常常会有这样的问题：在支付给员工的工资、薪金所得全年总额不变的情况下，每个月工资应该发放多少才能使全年工资、薪金所得的个人所得税金额最小。根据个人所得税法律法规的相关规定，工资、薪金所得个人所得税的应纳税额应按如下公式计算：

当应纳税所得额大于0时：

应纳税额=应纳税所得额×适用税率－速算扣除数

=(每月收入额-免税收入额-法定减除费用额-按规定可扣除的社会保险-按规定可扣除的住房公积金-按规定可扣除的捐赠等其他支出)×适用税率-速算扣除数

=(每月收入额-按规定可扣除项目金额总和)×适用税率-速算扣除数

=应纳税所得额×适用税率-速算扣除数

当应纳税所得额等于0时，应纳税额=0。

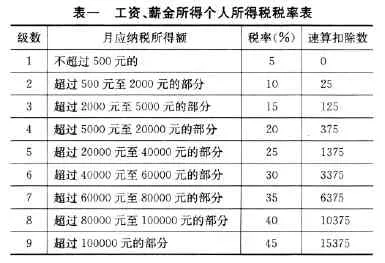
注：法定减除费用额指2000元或4800元。我们假设月应纳税所得额为0时其适用税率为0。月应纳税所得额大于0时其适用税率指其在表一中对应的最高税率，如月应纳税所得额为4000元时，其在表一中对应的最高税率为0.15，故0.15就是应纳税所得额为4000元时的适用税率，如没有特别说明，以下适用税率的含义与此相同。

?

由于工资、薪金所得适用超额累进税率，月应纳税所得额越大，适用的税率越大，故人们往往会觉得各月的工资发放较为平均时全年所交的个人所得税会较少，这时各月的应纳税所得额较为平均，其适用税率亦较为平均，故我们有命题1：在支付给员工的工资、薪金所得全年总额不变的情况下，若各月按规定可扣除项目金额总和是确定的且不发放全年一次性奖金，则当全年各月工资、薪金所得的月应纳税所得额的适用税率都相等时，全年各月工资、薪金所得的个人所得税应纳税额之和是最小的。

当我们考虑的时间不是一年而是若干个月时，情况又如何呢？由命题1我们不难有命题2：在支付给员工的m(m为大于0的整数)个月工资、薪金所得总额不变的情况下，若各月按规定可扣除项目金额总和是确定的且不发放全年一次性奖金，则当这m个月工资、薪金所得的各月应纳税所得额的适用税率都相等时，这m个月工资、薪金所得的个人所得税应纳税额之和是最小的。

二、命题的证明

命题1是命题2的特殊情形，只要令m=12，引用命题2就可以证明命题1，故只要证明了命题2，就可以证明命题1。

（一）命题2的证明如下：

设i为大于0且小于m+1的整数，第i月的应纳税额、应纳税所得额、收入额以及按规定可扣除项目金额总和分别为ti、yi、si、ai，其中ai是确定的正数。设各月应纳税额、应纳税所得额、收入额、按规定可扣除项目金额总和的m个月之和分别为Tm、Ym、Sm、Am，其中Sm是一大于或等于0的确定正数。由于ai是确定的正数，故Am是一确定的正数。

设当si=sdi时各月应纳税所得额的适用税率都相等，这时yi=ydi，ti=tdi，Tm=Tdm。设该相等的适用税率为d，d在表一中对应的速算扣除数为kd。

先用反证法来证明：若Sm、ai是确定的数值则d的值是唯一的。

假设d的值不是唯一的，即d可取两个或两个以上的值，取其中两个不同的值c、e，不妨设0≤c＜e。设当sdi=sci时，ydi=yci，d=c。设当sdi=sei时，ydi=yei，d=e。

由0≤c＜e可知yci≥sci－ai，yei=sei－ai。由表一可知，适用税率越大，其对应的应纳税所得额越大，故yci＜yei，故sci－ai＜sei－ai，故sci＜sei，故，这与Sm是一确定值矛盾，从而说明d可取两个或两个以上的值的假设不成立，也就是说d的值是唯一的，故kd的值亦是唯一的。

当d=0时，ydi=0，故tdi=0，故Tdm=0，由于Tm≥0，故Tdm是Tm的最小值。

由于Sm、Am都是确定的数值且d、kd的值亦是唯一的，故Tdm的值亦是唯一的。

在si-ai≤0的月份，si≤ai，ti=0，故si-sdi≤ai-sdi，因为d＞0，两边同乘d有d(si-sdi)≤d(ai-sdi)，即d(si-sdi)≤-dydi，两边同加tdi有tdi+d(si-sdi)≤tdi-dydi。由d＞0有kd≥0且tdi=dydi-kd，故tdi-dydi=-kd，故tdi－dydi≤0，故tdi+d(si-sdi)≤0，由于ti=0，故ti≥tdi+d(si-sdi)。

在si-ai＞0的月份，yi=si-ai=sdi-ai＋(si-sdi)=ydi＋(si-sdi)。若si-sdi≥0，因为月应纳税所得额为ydi时的适用税率为d，所以在此基础上增加si-sdi的月应纳税所得额时，该增加的月应纳税所得额的适用税率大于或等于d，故因此而增加的应纳税额大于或等于(si-sdi)d，由于月应纳税所得额为ydi时对应的应纳税额为tdi，故ti≥tdi＋(si-sdi)d。若si－sdi＜0，因为月应纳税所得额为ydi时的适用税率为d，所以在此基础上减少(sdi-si)的月应纳税所得额时，该减少的月应纳税所得额的适用税率小于或等于d，故因此而减少的应纳税额小于或等于(sdi-si)d，由于月应纳税所得额为ydi时对应的应纳税额为tdi，故ti≥tdi-(sdi-si)d，即ti≥tdi＋(si-sdi)d。

故d＞0时有ti≥tdi＋(si-sdi)d，故

综上所述，d≥0时Tdm是Tm的最小值。又因为d不能小于0，故命题2成立。

除命题2所述情形外，其他情形下这m个月工资、薪金所得的个人所得税应纳税额之和能否取得最小值呢？由上述证明可知，当所有月份都有ti=tdi＋(si-sdi)d时，Tm=Tdm，即这时Tm的值是最小的。ti=tdi＋(si-sdi)d意味着yi－ydi=si-sdi且yi-ydi的适用税率为d，这时yi的适用税率等于d或者d-0.05。所有月份的yi的适用税率等于d属于命题2所述情形。当yi的适用税率为d-0.05且d-0.05＞0时，要使ti=tdi＋(si-sdi)d，则yi必须等于表一中适用税率为d-0.05时的最大的月应纳税所得额，如d=0.2，则yi的适用税率等于0.15，yi=5000元；当yi的适用税率为d-0.05且d-0.05=0时，要使ti=tdi＋(si-sdi)d，则si必等于ai。由上述分析有命题3：在支付给员工的m(m为大于0的整数)个月工资、薪金所得总额不变的情况下，如果各月按规定可扣除项目金额总和是确定的，不发放全年一次性奖金，并且这m个月工资、薪金所得的月应纳税所得额分别适用两个不同的适用税率：d1及d2（d1、d2为大于或等于0的正数），d2减d1等于0.05，对于月应纳税所得额的适用税率为d1的月份增加的任意小的收入ε（ε为正数）元，该等月份因此而增加的应纳税所得额为ε元且其适用税率为d2，那么d2等于各月的月应纳税所得额的适用税率都相等时的适用税率且这m个月工资、薪金所得的个人所得税应纳税额之和是最小的。

（二）命题3的证明如下：

设月应纳税所得额大于b1（b1为大于或等于0的整数）且小于或等于b2（b2是大于0的整数）时其在表一中对应的适用税率为d2。设月应纳税所得额的适用税率为d1的月份有n（n为大于0且小于m的整数）个。设这m个月中第j（j为大于0且小于或等于m的整数）月的月应纳税所得额的适用税率为d2，设其月应纳税所得额为w，则b1＜w≤b2。

将第j月的工资收入减少(w-b1)/2且将其平均分配到月应纳税所得额的适用税率为d1的月份，其他月份的工资收入不作变动，故变化前后的工资收入总额不变。

进行上述变化后，第j月的工资收入减少了(w－b1)/2，该月份因此而减少的月应纳税所得额为(w-b1)/2，减少后的月应纳税所得额为w-(w-b1)/2＝(w＋b1)/2，由于b1＜w≤b2，故b1＜(w＋b1)/2≤(b2＋b1)/2＜b2，故减少后的月应纳税所得额的适用税率仍然为d2，故变化后减少的应纳税额为d2(w-b1)/2。

由b1＜w及n＞0可得(w-b1)/(2n)＞0。因为月应纳税所得额的适用税率为d1的月份增加任意小的收入ε元时，该等月份因此而增加的应纳税所得额为ε元且其适用税率为d2，所以进行上述变化后，月应纳税所得额的适用税率为d1的每一月份的工资收入都增加(w-b1)/(2n)，因此而增加的应纳税所得额为(w-b1)/(2n)且其适用税率为d2，即变化后该等月份的月应纳税所得额的适用税率变为d2，该等月份因此而增加的总的应纳税额为nd2(w-b1)/(2n)=d2(w-b1)/2，等于变化后第j月减少的应纳税额，而除第j月及月应纳税所得额的适用税率为d1的月份外，其他月份的应纳税额没有变化，故变化后这m个月工资、薪金所得的个人所得税应纳税额之和和变化前相等。由于月应纳税所得额的适用税率为d1的月份在上述变化后其月应纳税所得额的适用税率为d2，故变化后这m个月工资、薪金所得的各月应纳税所得额的适用税率都相等，由命题2的证明可知，该相等的适用税率的值是唯一的，故该相等的适用税率的值为d2，引用命题2可知变化后这m个月工资、薪金所得的个人所得税应纳税额之和是最小的，故变化前这m个月工资、薪金所得的个人所得税应纳税额之和亦是最小的，故命题3成立。

三、命题的应用

由于各月应纳税所得额都相等的时候，各月应纳税所得额的适用税率必相等，故只要求出各月应纳税所得额都相等时的月应纳税所得额，就可以得出各月应纳税所得额的适用税率都相等时的适用税率d，运用命题2及命题3就可以确定使m个月工资、薪金所得的个人所得税应纳税额之和最小的月应纳税所得额的取值范围。当d＞0时，设月应纳税所得额大于b（1b1为大于或等于0的整数）且小于或等于b（2b2是大于0的整数）时其在表一中对应的适用税率为d。具体运用步骤如下：

（一）若Sm-Am≤0，则最优工资发放方案为：各月的工资都少于或等于当月按规定可扣除项目金额总和。这时各月工资、薪金所得的个人所得税应纳税额m个月之和有最小值0。

（二）若Sm-Am＞0，各月应纳税所得额都相等时有Ym，这时各月的月应纳税所得额=Ym/m=(Sm-Am)/m，由表一可确定d、kd、b1及b2，则最优工资发放方案有两种：（1）每个月的月应纳税所得额都大于b1且小于或等于b2；（2）1个月以上（含1个月）m个月以下（不含m个月）的月应纳税所得额为b1，其余月份的月应纳税所得额都大于b1且小于或等于b2。由命题2的证明可知，这时各月工资、薪金所得的个人所得税应纳税额m个月之和有最小值(Sm-Am)d-mkd。

（三）将每月的应纳税所得额加上每月按规定可扣除项目金额总和就可以得出每月的工资发放额。

如某人20x9年预计全年工资收入为81600元，每月税前可扣除的社会保险费为300元，1至6月每月税前可扣除的公积金为500元，7至12月每月税前可扣除的公积金为600元，每月都没有免税收入及税前可扣除的捐赠等其他支出，假定每月的法定减除费用额为2000元，则m=12，S12=81600（元），A12=300×12+500×6+600×6+2000×12=34200（元），各月应纳税所得额都相等时的月应纳税所得额=(S12－A12)/12=(81600-34200)/12=3950（元）。由表一可知d=0.15，b1=2000（元），b2=5000（元），kd=125，故最优工资发放方案有两种：（1）每个月的月应纳税所得额都大于2000元且小于或等于5000元；（2）1个月以上（含1个月）12个月以下（不含12个月）的月应纳税所得额为2000元，其余月份的月应纳税所得额都大于2000元且小于或等于5000元。这时全年各月工资、薪金所得的个人所得税应纳税额之和的最小值是(81600－34200)×0.15－125×12=5610（元）。将每月的应纳税所得额加上每月按规定可扣除项目金额总和就可以得出每月的工资发放额（具体计算过程略）。