有穷非整数级亚纯函数的唯一性定理

翟广鹏 李娜

（山东省莘县供电公司,山东莘县252400）

有穷非整数级亚纯函数的唯一性定理

翟广鹏 李娜

（山东省莘县供电公司,山东莘县252400）

本文利用Nevanlinna基本定理，得到一个关于有穷非整数级亚纯函数的唯一性定理，推广了现有的结果。

亚纯函数；分担值；唯一性

1.引言

整函数与亚纯函数是函数论的一大分支，值分布理论是整函数与亚纯函数所研究的主要内容之一，而函数的唯一性理论是值分布理论的一个重要研究方向.我国数学界在值分布论的研究中，在二十世纪三四十年代，熊庆来、李国平、庄圻泰等老前辈就做出了许多独创的成果。近二三十年来，我国著名的数学家杨乐、张广厚、顾永兴、陈怀惠、仪洪勋等也在这方面研究获得了许多新进展，在国际上走在前列［1-16］。在本文，我们首先介绍了研究亚纯函数的唯一性理论的重要工具—Nevanlinna基本理论，以及现有的成果，最终得到了两个关于有穷非整数级亚纯函数的唯一性定理。

首先给出标记符号：标记符号［1］设f（z）与g（z）与为非常数亚纯函数，a为任意复数.再设f（z）-a的零点为zn（n=1，2，…）。如果zn（n=1，2，…）也是g（z）-a的零点（不计重级），则记为f=a⇒g=a或g=a⇐f=a.如果zn（n=1，2，…）是f（z）-a的v（zn）重零点时，zn（n=1，2，…）也是g（z）-a的至少v（zn）重零点，则记为f=a→g=a或g=a←f=a.因此f=a⇔g=a表示f（z）-a与g（z）-a的零点相同（不计重级），f=∞⇔g=∞表示f（z）与g（z）的极点相同（不计重级）。f=a⇌g=a表示f（z）-a与g（z）-a零点相同，而且每个零点的重级也相同，f=∞⇌g=∞表示f（z）与g（z）的极点相同而且每个极点的重级也相同.

定义1.1［1］设f（z）与g（z）为非常数亚纯函数，a为任意复数.

i）如果f=a⇌g=a，则称a为f（z）与g（z）的CM公共值.（也称f（z）与g（z）CM分担a［12］）

ii）如果f=a⇔g=a，则称a为f（z）与g（z）与的IM公共值.（也称f（z）与g（z）IM分担a［12］）

iii）如果a为f（z）与g（z）的IM公共值，并且f（z）-a与g（z）-a的所有零点的重级均不相同，则称a为f（z）与g（z）的DM公共值.

1.2［2］设k是一个非负整数或∞，a∈c，Ek（a，f）表示f-a的所有零点，当零点的重数m≤k，计m次；若m＞k，则计k+1次，如果Ek（a，f）=Ek（a，g），那么称f与g以权k分担a.

1.3［4］［8］设f（z）为亚纯函数，按照约定f（z）不为常数，因而当r→∞时，T（r，f）→∞，对任意复数a（可以为∞）我们定义：

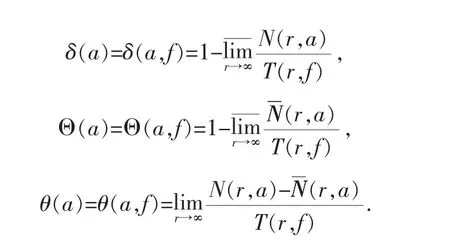
δ（a，f）、θ（a，f）分别称为f（z）的亏量、f（z）的a值点的重级指数，如果δ（a，f）＞0，则称a是f（z）的一个亏值或一个Nevanlinna例外值.显然，有0≤δ（a）≤Θ（a）≤1，0≤θ（a）≤Θ（a）≤1.

下面给出Nevanlinna基本定理和已有结果.

定理1.1［1］（Nevanlinna第二基本定理）设f（z）是圆内的亚纯函数，f（0）≠0，1，∞，

且f′（0）≠0.则对0＜r＜R有

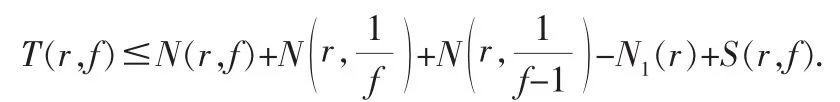
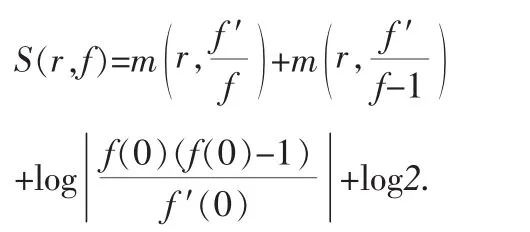
采用精简密指量（精简计数函数［1］）的定义以后，第二基本定理的等价形式为

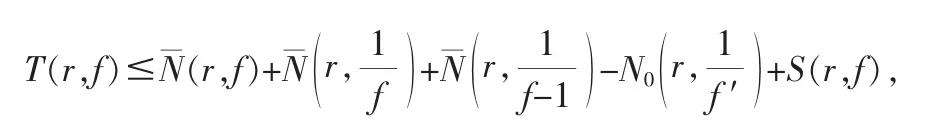
对于有穷非整数级整函数，仪洪勋［5］证明了：

定理1.2［5］设f（z）与g（z）为非常数整函数，f（z）的级λ（f）为有穷非整数，且f=0⇌g=0.如果存在两个判别的有穷非零复数a1，a2，满足及则

2.几个引理

引理2.1［4］设f（z）和g（z）是两个亚纯函数，它们的级分别为λ（f）和λ（g），若λ（f）＜λ（g）,则f（z）±g（z）的级

引理2.2［4］设f（z）是一个亚纯函数，则亚纯函数与f（z）=的级相同.特别是与f（z）有相同的级.

引理2.3［4］设f（z）和g（z）是两个亚纯函数，它们的级分别为λ（f）和λ（g），若λ（f）＜λ（g）,则亚纯函数f（z）·g（z），的级λ都与g（z）的级λ（g）相等.

引理2.4［1］设f（z）和g（z）为开平面上的非常数亚纯函数，其级分别为λ（f）和λ（g），则

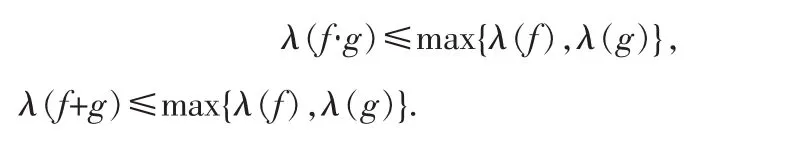
引理2.5［5］设h（z）为非常数整函数，f（z）=eh（z），且f（z）的级为λ，下级为μ，

i）若h（z）为p次多项式，则λ=μ=p.

ii）若h（z）为超越整函数，则λ=μ=∞.

引理2.6设f（z）和g（z）为有穷非整数级亚纯函数，f（z）的级λ（f）与g（z）的级λ（g），满足λ（f）≤λ（g），且，则λ（f）=λ（g）.

证明由条件λ（f）≤λ（g）知，只需证明λ（f）＜λ（g）不成立即可.

1°若f（z）≡g（z），则显然λ（f）=λ（g）.

2°若f（z）不恒等于g（z），用反证，假设λ（f）＜λ（g）成立.由于f=0⇌g=0，故可设其中h（z）为整函数.由已知，eh（z）不恒为1，故由引理2.3，由引理2.5知，上式左边是整数，而右边是有穷非整数，显然不能成立，从而λ（f）＜λ（g）的假设不成立，只能有λ（f）=λ（g）.

综合1°、2°，引理2.6得证.

引理2.7[6]设f，g是非常数亚纯函数，λ（g）为有穷非整数，且f，g具有两个CM公共值0，∞，如果存在两个判别的有穷非零复数a1，a2满足

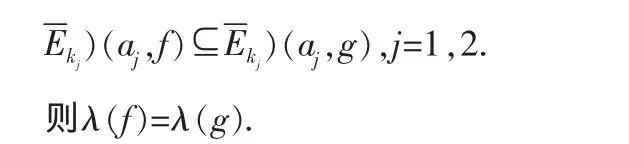
3.主要结果及其证明

接下来，我们要对定理1.2进行改进：关于整函数的唯一性定理推广为关于亚纯函数的唯一性定理.从而得到如下定理：

定理3.1设f（z）和g（z）是两个非常数亚纯函数，g（z）的级λ（g）为有穷非整数，且如果a1，a2是另外的两个判别的有穷非零复数，满足及则

证明（1）不妨设b1=0，b2=∞.假设f（z）不恒等于g（z），由已知条件及引理2.7，得λ（f）=λ（g）.又f=0⇌g=0，故可设

其中h（z）为整函数，由引理2.2和引理2.4，

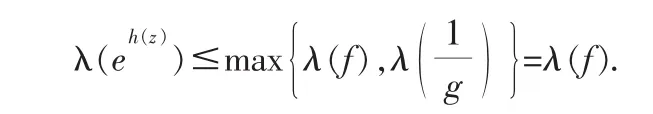
设{zn}是f（z）-a1的所有j（1≤j≤k）重零点，则由f=a1→g=a1知，其中k为任意正整数，故{zn}也是g（z）-a1的j（1≤j≤k）重零点，由，得eh（zn）=1.

由假设f（z）不恒等于g（z），则eh（z）不恒为1，从而有

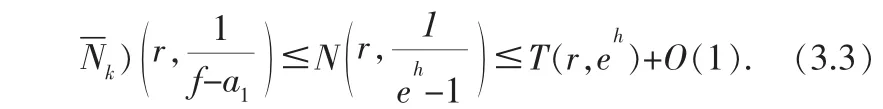
同理，

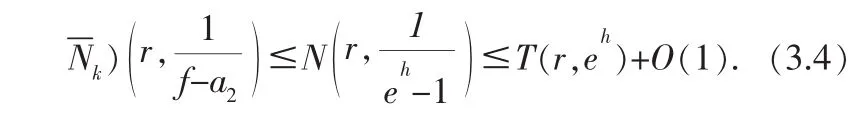
其中k为任意正整数.

由Nevanlinna第二基本定理，得

从而

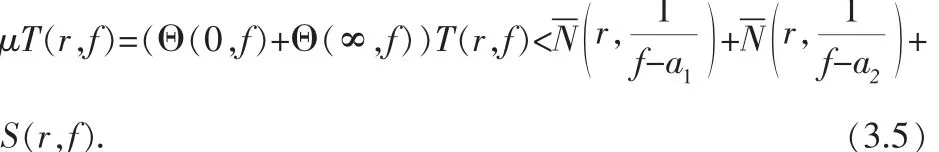
而

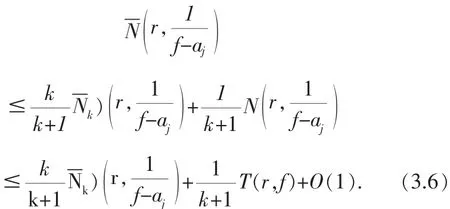
其中，j=1，2，由（3.3）、（3.4）、（3.5）和（3.6）式得

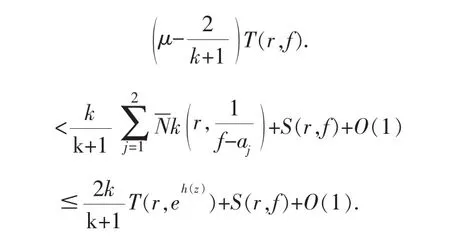
上式两边中令k→∞，则

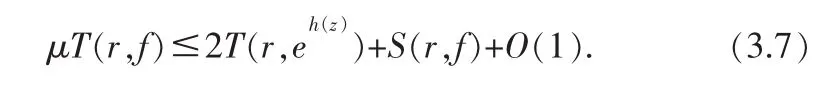
因此λ（f）≤λ（eh（z））与（3.2）式矛盾，假设不成立.故f（z）≡g（z）.

（2）b1，b2均为有穷非零复数，则令

则有λ（F）=λ（f），λ（G）=λ（g），显然，F，G满足（1）的情形，其它情形均可转换为（1）的情形.

由（1）、（2），结论得证。

［1］仪洪勋，杨重骏.亚纯函数唯一性理论［M］.北京：北京大学出版社，1995：24-132.

［2］林珊华，林伟川.整函数涉及权分担值的微分多项式唯一性问题［J］.福建师范大学学报（自然科学版），2005,21（4）：22-26.

［3］林伟川.涉及亚纯函数正规族与唯一性理论的几个问题［D］.济南：山东大学，2003：5-6.

［4］柏盛桄.整函数与亚纯函数［M］.湖北：华中师范大学出版社，1987：93-146.

［5］林伟川.涉及零点分布整函数的唯一性［J］.纺织高校基础科学学报，2001,14（4）：283-285.

［6］吕巍然，林伟川.整函数惟一性定理的一个推广［J］.石油大学学报（自然科学版），2002,26（4）：106-108.

［7］张南岳，陈怀惠.复变函数论选讲［M］.北京：北京大学出版社，1995.8：283-290.

［8］莫叶.亚纯函数论［M］.济南：山东大学出版社，1997.5：48-49.

［9］张国威.亚纯函数唯一性及正规族［D］.硕士学位论文，济南：山东大学，2008.3.10：8-9.

［10］王品玲.整函数和亚纯函数值分布的若干结果［D］.博士学位论文，南京：南京师范大学，2006：7.

［11］黄斌.具有四个分担值的亚纯函数的唯一性定理（英文）［J］.数学季刊,2001,16（4）：35-42.

［12］黄斌.具有一个或两个分担值的亚纯函数的唯一性［J］.山东大学学报（理学版）,2002,37（2）：111-114.

［13］林珊华，林伟川.整函数涉及权分担值的微分多项式唯一性问题［J］.福建师范大学学报（自然科学版），2005,21（4）：22-26.

［14］Yi hongxun.Unicity theorems for entire or meromorphic functions［J］.Acta Mathematica Sinica,1994,10（2）：121-131.

［15］杨乐.值分布理论及其新研究［M］.北京：科学出版社，1982：5.

［16］林伟川，吕巍然.有穷级整函数的唯一性［J］.福建师范大学学报（自然科学版），2001,17（2）：6-9.

book=4,ebook=65

O174.52

A

1008—3340（2010）04—0061—03

2010－10－21

翟广鹏（1987－），男，本科，山东省莘县供电公司。李娜（1986－），女，本科，山东省莘县供电公司。