一阶线性微分方程解的渐进性证明

袁春华

（济南大学理学院，山东 济南 250022）

一阶线性微分方程解的渐进性证明

袁春华

（济南大学理学院，山东 济南 250022）

本文给出了一阶线性微分方程解的渐近性证明常用的结论并对结论进行了证明，通过举例说明了应用这些结论证明一阶线性微分方程解的渐进性非常简便。

一阶线性微分方程；初值问题；连续

1.基本知识

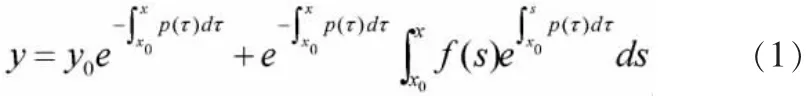
2.基本结论

对于满足一定条件的一阶线性微分方程，可以利用一阶线性微分方程解表达式（1），对一阶线性微分方程解的渐进性进行证明，证明时，常用到如下的相关结论．

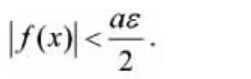
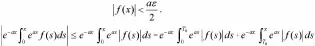
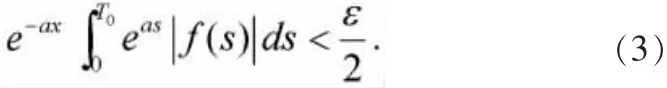
则对上述任给ε>0，取T=max{T0，T1}，当x>T时，由式（2）、（3）可知：

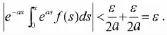
证明：令F（x）=f（x）-b，则F（x）在［0，+∞）上连续，且有由结论1可知：=0.

从而

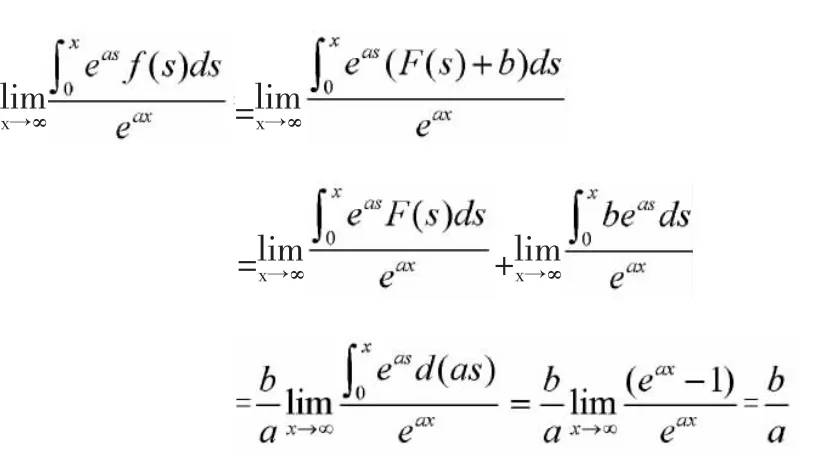
3.结论应用

证明：不妨设y=y（x）是方程任一解且满足 y=（0）=y0，初值问题满足解的存在唯一性条件，由（1）式可知，该初值问题的解为：

则

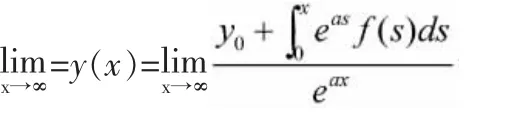
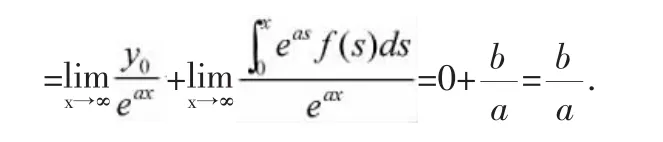
例2：设f（x）在［0，+∞）上连续可微，

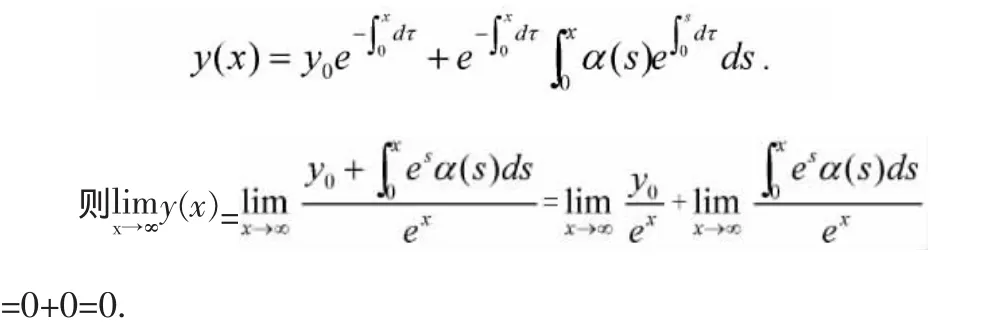
4.小结

对上述例题，也可以直接用函数极限定义直接证明，但非常麻烦；利用上述结论证明有关一阶线性微分方程解的渐进性非常方便简捷。

［1］东北师范大学微分方程教研室.常微分方程［M］.北京：高等教育出版社，2009.

［2］王克，潘家齐.常微分方程学习指导书［M］.北京：高等教育出版社，2007.

［3］庄万.常微分方程习题解［M］.济南：山东科学技术出版社，2008.

［4］王高雄，周之铭，朱思铭，王寿松.常微分方程［M］.北京：高等教育出版社，2004.

book=59,ebook=1

O175

A

1008—3340（2010）04—0059—02

2010－08－28

袁春华（1967-），男，讲师，硕士，研究方向：交通规划、智能优化算法。