用变分迭代法求解Hirota-Satsuma型耦合KdV方程组

于欢欢,张金良

用变分迭代法求解Hirota-Satsuma型耦合KdV方程组

于欢欢,张金良

(河南科技大学数学与统计学院,河南洛阳471003)

用变分迭代法研究了Hirota-Satsuma型耦合 KdV方程组,求出了 Hirota-Satsuma型耦合 KdV方程组的近似解,利用Matlab对近似结果和精确解进行了模拟.

变分迭代法;Hirota-Satsuma型耦合KdV方程组;Matlab;模拟

变分迭代法来源于量子力学,后来被工程师Inokuti[1]等应用于求解非线性方程,取得了比较理想的效果.但是,由于这种方法识别Lagrange乘子很繁杂,一直未得到普遍的关注和应用.1999年,何吉欢[2]对广义的拉格朗日乘子做了修正,引入限制变分的概念,提出一种简单而快速的变分迭代方法:首先设初始迭代为含有若干参数的等式,然后利用一般的Lagrange乘子来构造修正函数,这里通过变分原理[3]确定Lagrange乘子的最优值.变分迭代法能够得到真实解的一个收敛的连续逼近解,而且变分迭代法不受任何限制,如线性和非线性问题中的小参数限制等.它以类似的方式处理线性问题和非线性问题,而且其收敛性也得到了验证[4].

近年来许多学者对变分迭代方法作了大量的研究,一些研究人员将其用于求解非线性的积分微分方程[5]、KdV方程[6]、量子力学中的微扰问题[7]、厄尔尼诺/拉尼娜-南方海涛模型[8]、海-气振子ENSO模型[9]、厄尔尼诺大气物理机理上的一些问题[10]以及研究赤道海气振子模型[11]等,也有学者将变分迭代方法与现存的方法进行了比较,结果证明变分迭代法收敛到真实解的速度较快[12].本文利用变分迭代方法求解广义的 Hirota-Satsuma型耦合 KdV方程组的近似解,并利用Matlab对其近似结果和精确解进行模拟.

1 求解Hirota-Satsuma型耦合KdV方程组

在文献[13]中介绍了含有三个位势的4×4阶矩阵的谱问题,其中一种类型的方程为广义的 Hirota-Satsuma型耦合 KdV方程.近年来,许多学者用不同的方法对广义的 Hirota-Satsuma型耦合KdV方程进行了研究,如扩展的tanh函数展开法[14]、符号计算法[15]以及代数方法[16]等.

考虑一个广义的Hirota-Satsuma型耦合 KdV方程组

初始条件为

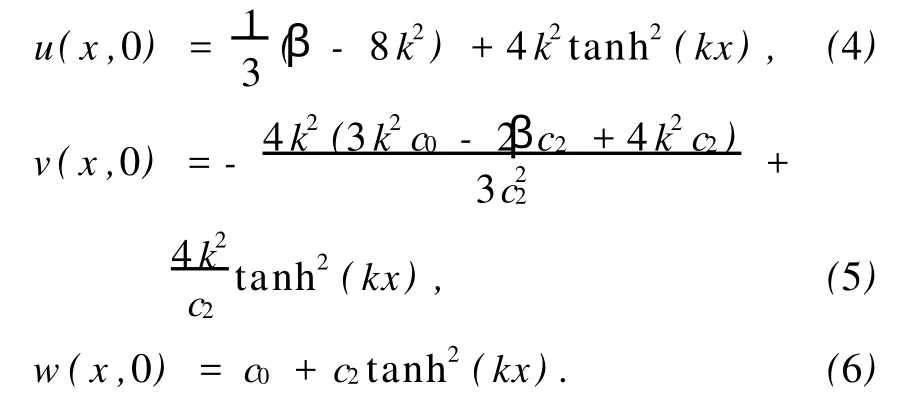
式中c0,c2,β和k均为常数.它的精确解为

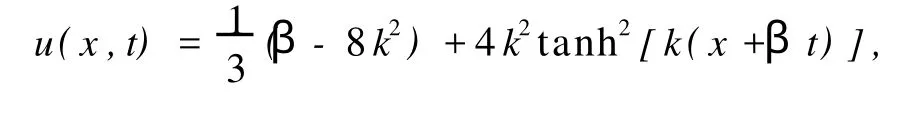
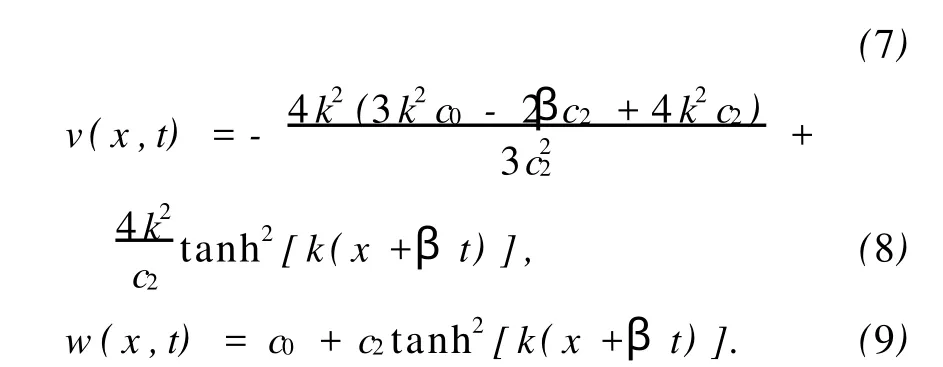
用变分迭代方法对方程(1)～(3)建立如下校正泛函

式中λ1,λ2和λ3是广义的拉格朗日乘子和为限制变分量,即δ

对式(10)～(12)取变分得

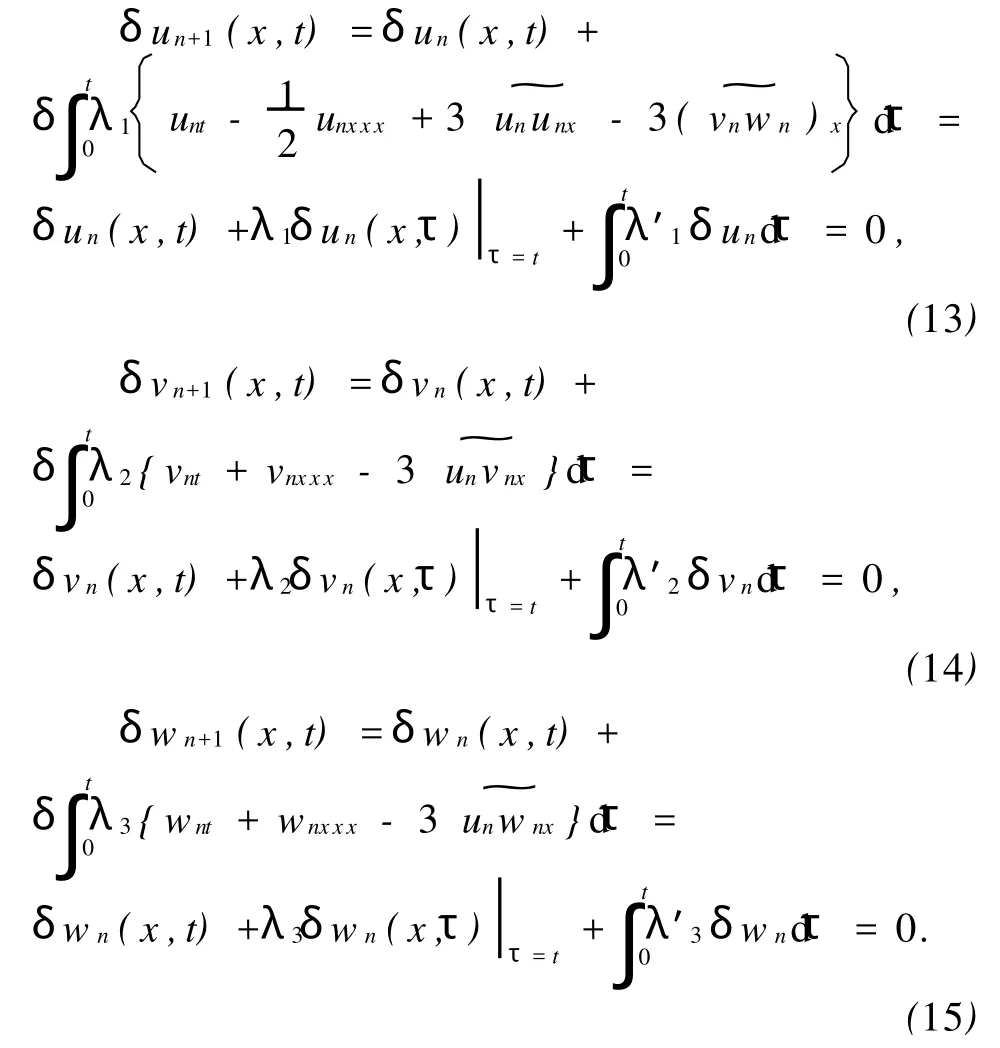
于是,可得以下驻值条件

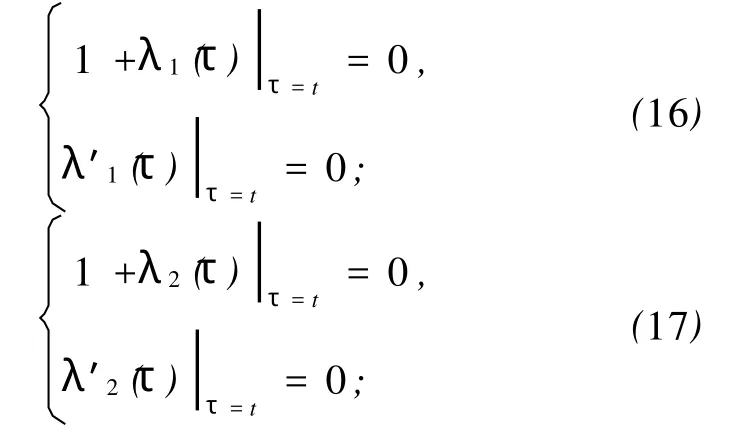
从而,可以识别拉氏乘子得

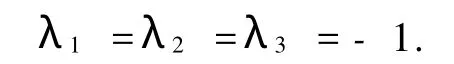
将其代入到式(10)～(12)得到迭代公式

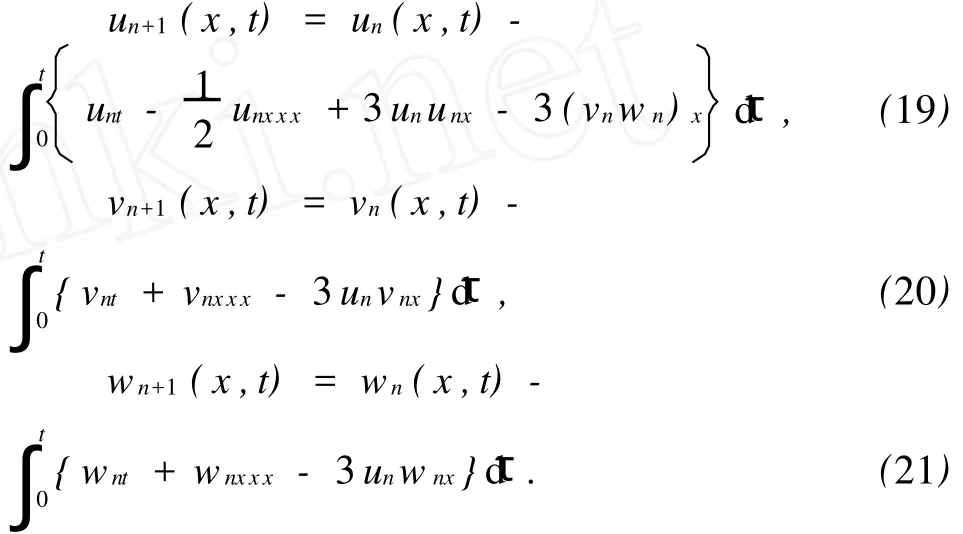
假设初始近似解为

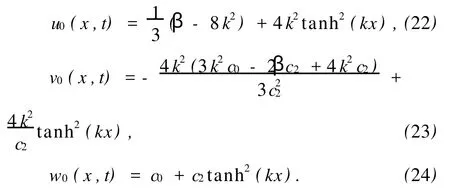
令分别将式(16)、(17)、(18)代入到式(13)、(14)、(15)得到

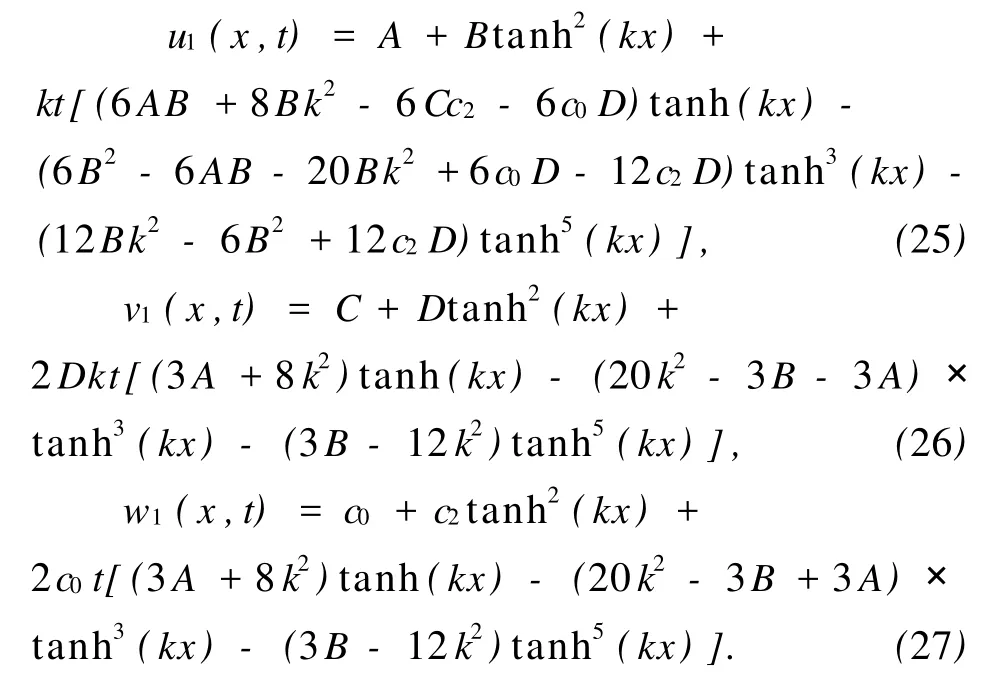
由于c0,c2,β和k均为常数,这里令β=2,c0= c2=k=1,则有

A=-2,B=4,C=-4,D=4.

于是方程的近似解(25)～(27)为

同理,将式(28)～ (30)带入变分迭代公式(19)～ (21)得到

利用变分迭代公式(19)～ (21),还可以计算出三阶以及更高阶的近似解.

当β=2,c0=c2=k=1时,方程(1)～(3)的精确解为

利用Matlab,方程组(1)～ (3)的精确解和近似解见图1～图9.

图1 β=2,c0=c2=k=1时,u(x,t)的精确解图像

2 结束语

由模拟结果可以看出,用变分迭代法求解广义Hirota-Satsuma耦合 KdV方程组,一阶迭代近似解的图形与精确解吻合的相当好,由此可以根据近似解来研究广义 Hirota-Satsuma耦合 KdV方程组孤波的波形变化和特征.但是,在进一步迭代的时候,由于t的幂次高,所得近似解的图形与精确解偏差较大.这也说明变分迭代方法在应用中有一定的局限性,但仍是解决这类问题的强有力工具.

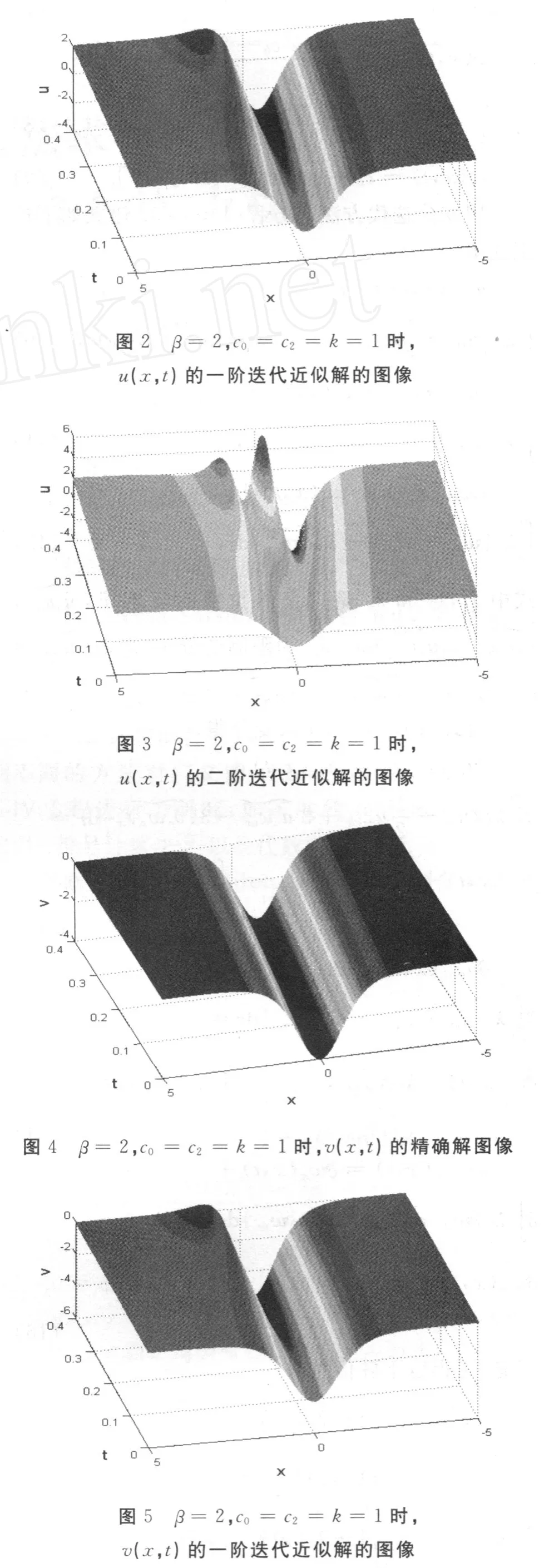
[1]Inkuti M,Sekine H,Mura T.General use of the Lagrange multiplier in nonlinear mathematical physics,in variational method in the mechanics of solids[M].Pergamon Press,1978:156-162.

[2]He J H.Variational iteration method-Some recent results and new interpretions[J].Computers and Mathematics with Applications,2007,54:881-894.

[3]徐建平,桂子鹏.变分方法[M].上海:同济大学出版社,1999:5-35.

[4]Tatari M,Dehghan M.On the convergence of He’s variational iteration method[J].Journal of Computational and Applied Mathematics,2007,207:121-128.

[5]Odibat Z M,Momani S.Application of variational iteration method to Nonlinear differential equations of fractal order[J].International Nonlinear Science and Numerical Simulation,2006,7:27-34.

[6]Inc M.Numerical simulation of KdV andmKdV equations with initial conditions by the variational iteration method[J].Chaos Solitons and Fractals,2007,34(4): 1075-1081.

[7]谢长珍.变分迭代法求解量子力学中的微扰问题[J].江西科学学报,2004,22(5):317-322.

[8]莫嘉琪,林万涛,朱江.厄尔尼诺/拉尼娜一南方海涛模型的变分迭代解法[J].数学进展,2006,35(2):232-236.

[9]冯茂春.海-气振子 ENSO模型的变分迭代解法[J].中山大学学报:自然科学版,2005,44(增刊):152-153.

[10]莫嘉琪,林万涛.厄尔尼诺大气物理机理的变分迭代解法[J].物理学报,2005,54(3):1081-1083.

[11]莫嘉琪,林万涛.三维赤道海气振子模型的近似解[J].物理学报,2008,57(3):1291-1294.

[12]Wazwaz A M.A comparison between the variational iteration method and Adomian decomposition method [J].Journal of Computational and Applied Mathematics,2007,207(1):129-136.

[13]Wu Y T,Geng X G,Hu XB,et al.A generalized Hirota-Satsuma coupled Korteweg-de Vries equation and Miura transformations[J].Physics Letters A,1999, 255:259-264.

[14]Malfliet W.Solitary wave solutions of nonlinear wave equations[J].Am.J.Phys.,1992,60:650-654.

[15]Lan Xu.Variational iteration method for solving integral equations[J].Computers and Mathematics with Applications,2007,54:1071-1078.

[16]Zayed E M E,Zedan H A,Gepreel K A.On the solitary wave solutions for nonlinear Hirota-Satsuma coupled KdV equations[J].Chaos Solitons and Fractals,2004,22(2):285-303.

[17]何吉欢.Schrodinger方程的变分迭代解法[J].数学物理学报,2001,21A(增刊):577-583.

[18]谢元喜,唐驾时.求一类非线性偏微分方程精确解的简化试探函数法[J].动力学与控制学报,2005,3(1): 15-18.

[19]Parkes E J,Duffy B R.An automated tanh-function method for finding solitary wave solutions to nonlinear evolution equation[J].Computer Physics Communications,1996,98:288-300.

Variational iteration method for solving the Hirota-Satsuma coupled KdVequations

YU Huanhuan,ZHAN GJinliang
(School of Mathematics and Statistics,Henan University of Science and Technology, Luoyang 471003,China)

In this paper,the variational iteration method were applied to investigate the Hirota-Satsuma coupled KdV equations,and some approximate solutions were obtained.Using Matlab,the approximate solutions and exact solutions of the Hirota-Satsuma coupled KdV equations were simulated.

variational iteration method;Hirota-Satsuma coupled KdV equations;Matlab;simulation

O175.2

A

1671-9476(2010)05-0038-04

2010-05-12

河南省基础与前沿技术研究项目(No.092300410179);河南科技大学博士启动基金资助项目(No.09001204)

于欢欢(1986-),男,河南通许人,硕士研究生,主要从事非线性数理方程研究;张金良(1966-),男,河南唐河人,教授,博士,研究方向:非线性数学物理问题.