加工中心龙门磁悬浮高度的滑模-H∞控制*
刘春芳 安明伟 王丽梅
(沈阳工业大学电气工程学院,辽宁沈阳 110023)
加工中心龙门磁悬浮高度的滑模-H∞控制*
刘春芳 安明伟 王丽梅
(沈阳工业大学电气工程学院,辽宁沈阳 110023)
针对龙门数控加工中心中移动横梁的悬浮高度进行了研究。在龙门移动式数控机床中,可采用磁浮技术悬浮横梁消除摩擦提高加工精度。为保持悬浮系统的稳定性和精确性,提出了自适应积分滑模控制器并结合鲁棒H∞控制理论的控制方案。针对系统参数摄动和未建模动态设计了积分滑模变结构控制器;为降低滑模控制器抖振的发生,采用自适应控制对控制律的不确定值进行估测;考虑到刀具切削部件引起的系统质量变化以及外力干扰等对系统的影响,在控制中结合了H∞的控制理论,以增加系统的鲁棒性。仿真研究结果表明,此控制器具有很强的抑制扰动的能力和高刚度,可以实现稳定悬浮。
磁悬浮系统 反馈线性化 滑模变结构 自适应控制
随着工业技术的进步,磁悬浮系统应用越加广泛,而且多应用于高精密用途。许多精密仪器及工业设备均使用磁悬浮系统,因此对于定位控制的精密度要求也越来越高。如何选择有效的控制法则,使受控的磁悬浮系统达到要求,就成为精密定位控制的重要课题[1,2]。本文将磁浮技术应用于龙门数控加工中心以电磁铁和静止导轨之间产生的吸力为基础将龙门的横梁悬浮在静止导轨上方,同时采用永磁直线电动机进行推进驱动即能够实现高精度定位。
本文采用反馈线性化理论,将磁悬浮非线性系统转换为特定的线性系统,再针对转换的线性状态进行控制,来达成位置追踪定位控制的目的。在控制器设计部分,本文先对系统设计出滑模控制器,然后再根据适应控制理论针对滑模控制器的参数不确定值进行估测。目的主要是降低滑模控制器抖振的发生,使所设计的自适应滑模控制器有良好的暂态响应和稳态误差。同时,对系统所面临的刀具切削引起的系统质量改变以及外力扰动等的抑制问题,提出自适应积分滑模控制器结合鲁棒控制理论∞来抑制这种扰动,以增强系统的鲁棒性。经仿真验证得,此控制器能有效估测系统参数、具有小稳态误差及高鲁棒性且能使系统达到精确定位及追踪目的。
1 磁悬浮机床的单铁动力学模型及线性化方法
1.1 数学模型
龙门移动式横梁两端垂直同步悬浮,除了要求悬浮的高刚度以外,还要保证悬浮的同步性、稳定性和精确性。通过理论分析,可以得出磁悬浮机床的每一个电磁铁都有独立控制自由度。因此系统可以解耦为单电磁悬浮的控制问题[3]。其动力学模型如图1所示。
忽略铁芯的边际效应(Field Fringing)及漏磁(Leakage Flux),忽略铁芯和导磁物之间的磁阻,假设磁化曲线是线性的,认为磁通密度及磁场强度在铁芯及气隙中都是均匀分布的。
因此单电磁铁悬浮非线性动力学模型方程为
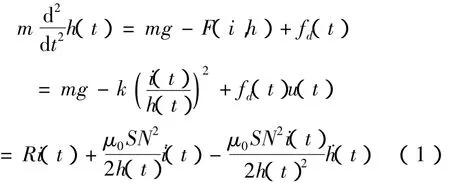

式中:h(t)表示悬浮间隙;F(i,h)表示电磁吸力;m 表示悬浮横梁的质量;g为重力加速度;fd(t)为干扰;i(t)为控制线圈的电流;u(t)为控制线圈两端的电压;μ0=4 ×10-7为真空磁导率;S为铁心面积;N为电磁铁绕组匝数;k=μ0SN2/4是一个常量。
1.2 反馈线性化方法
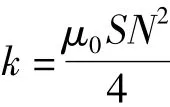


那么非线性状态空间方程可以写为
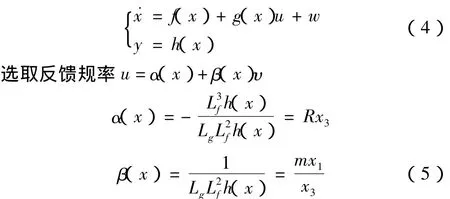
设线性状态变量为z=[z1z2z3]T,又根据˙z=[∂Φ(x)/∂x][f(x)+g(x)α(x)+g(x)β(x)υ]我们可以得到线性状态空间方程

2 自适应积分滑模鲁棒控制器设计
在研究磁悬浮系统控制的过程中会遇到两种不确定因素:第一种是系统的参数随环境变化而造成的参数摄动以及建模过程中被忽略的未建模动态;第二种是悬浮刀具切削工件引起的悬浮体质量改变以及外力扰动[3]。
针对磁悬浮系统在控制器设计上必须考虑磁浮系统中这些不确定性的影响,才能设计出抗扰性和鲁棒性高的控制器。对此,本文设计了自适应积分滑模鲁棒控制器。
2.1 积分滑模控制器
设φu为受到的等效外力扰动,则线性状态方程式(6)变换为



式中:G为常数矩阵;v=v0+v1,v0为系统连续控制;v1为系统不连续控制。
由文献[5]可知,任一矩阵 B∈Rn×m,若 rankB=m,则矩阵B可满足特性

式中:B+为 B 的伪逆矩阵(Pseudo Inverse Matrix),B+=(BTB)-1BT;B⊥为 BT的零空间,B⊥∈Rn×(n-m)。
将系统总扰动量φ写成以下形式φ=φm+φu,其中 φm≡BB+φ,φu≡B⊥B⊥+φ。这里 φm代表系统的未建模动态、系统参数摄动等扰动;φu代表刀具切削引起的悬浮横梁系统质量变化或受到的外力扰动。
将式(10)微分,可得

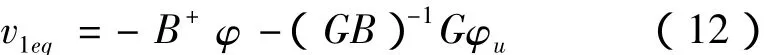
将 v1以式(12)替代并代入式(9)得

其中矩阵 Γ =[I-B(GB)-1G],等效干扰 φeq=Γφu。
从式(13)中得,扰动φm已成功被消除,只剩下扰动φu,因此必须借由调整矩阵G和设计v0来抑制由于质量变化等引起的扰动对系统的影响。
依据文献[5],可知当G=B+时,可将等效干扰抑制到最小。此时‖Γ‖=1,φeq=φu。因此可将此结果带到等效控制式(12)中,得

式(14)中仅包含φm,因此若想使用不连续控制v1补偿φu将会使得系统稳定性变得更不好。
这里使用不连续控制

其中ρ为切换增益。之后再以G=B+代入滑模函数,并微分一次,得

检验式(16)稳定性。定义Lyapunov函数为

将上式微分一次
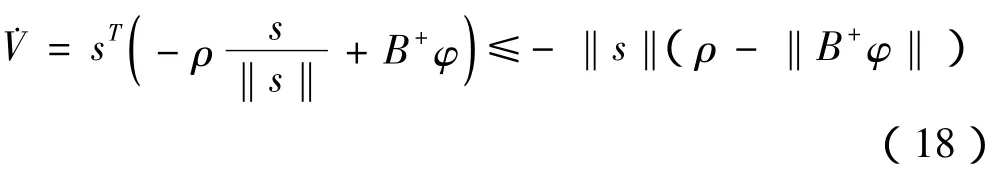
其中ρ>‖B+φ‖,故系统满足Lyapunov稳定。
2.2 自适应估测法则
磁悬浮系统在定位控制以及追踪命令时,会存在扰动φm,且其不是固定不变的。这会使系统不稳定抖振剧烈,无法精确的追踪和定位。因此,根据自适应控制原理设计一个自适应法则,估测滑模控制器控制律中切换函数项扰动参数值的上界,以降低系统的抖振现象,使系统输出能够追随输入命令运行。
因为未建模动态或系统参数摄动扰动的上界未知,因此假设此扰动为有界函数,其上界为,|φm|≤。然后根据适应控制原理设计的一个自适应法则去估测此扰动的上界¯φm,其估测值为^φ。其自适应估测法则为

其中β为自适应增益,β>0。
2.3 H∞控制
虽然前面所设计的自适应积分滑模控制器有良好的暂态性能和稳态误差,但是只要系统质量变化,即不确定因素φu存在时,则可能造成磁浮系统不稳定。因此针对式(13)中扰动φeq=φu的抑制,本论文采用H∞控制理论来处理。
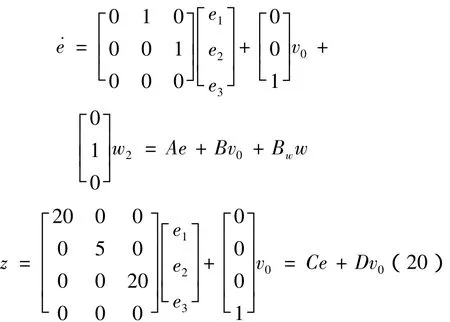
考虑下列系统式中z为所要调节的输出,C和D分别为状态和输入的加权矩阵。这里的控制目标是使扰动w以及输出z的转移函数Tzw的H∞范数压缩至最小。
接下来再按照H∞控制的设计方式,找出γ值。

式中γ=20.35时,可满足式(21)。
求半正定对称矩阵X,满足代数Riccati方程式

可求出矩阵

若找出矩阵X,则控制器可设计为
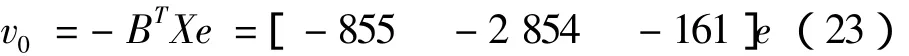
再将式(15)与式(23)合并及应用自适应估测法则可得控制律
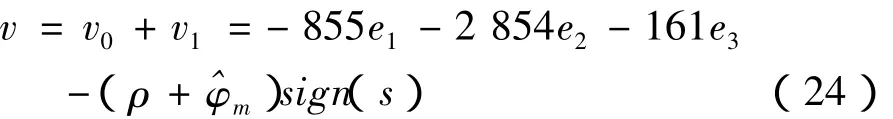

此控制律即是磁浮系统反馈线性化自适应积分滑模鲁棒控制的法则。其结构图如图2所示。
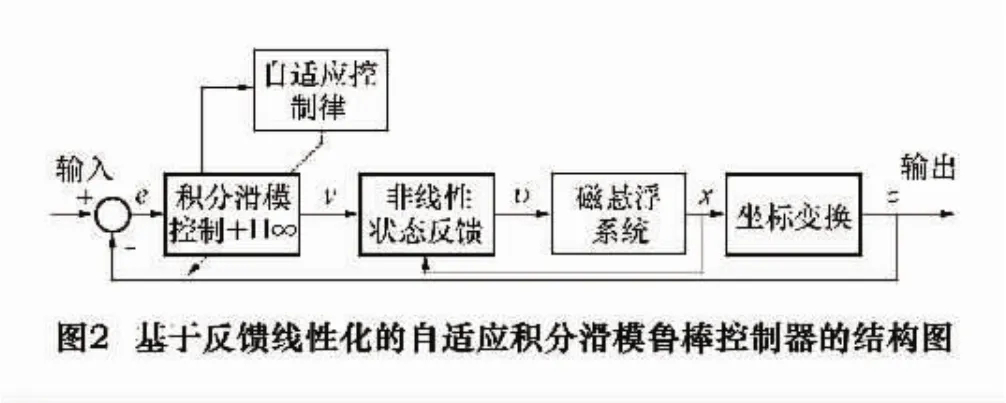
稳定性分析:
定义Lyapunov函数为
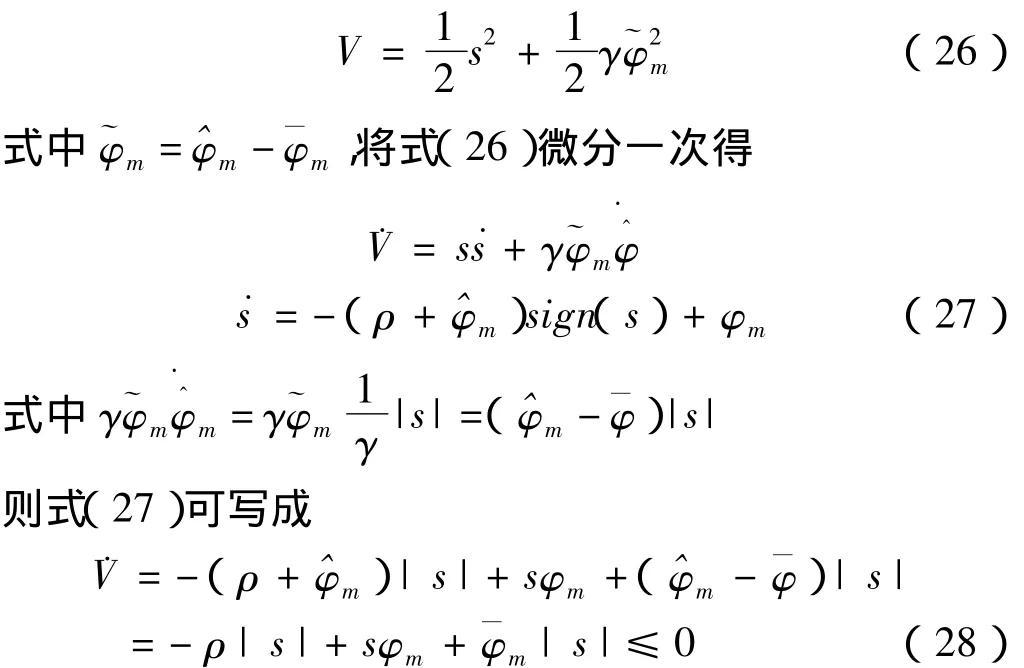
则满足稳定理论。
3 仿真
为了实现机床高加工精度的目标,将横梁悬浮起来,要求所设计的滑模控制器能够使横梁稳定地悬浮在2 mm处,并在有扰动影响的情况下具有很强的鲁棒性。根据上面所设计的控制器,利用MATLAB/Simulink进行仿真[11]。系统参数见表1。
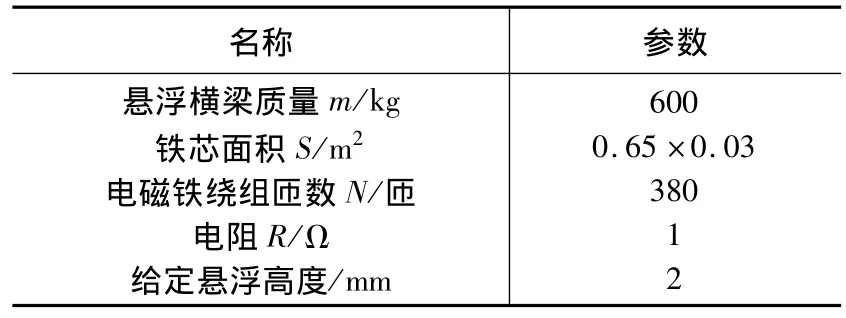
表1 系统参数
在仿真过程中,系统的稳定性和滑模面及控制率中的参数有密切的关系,要选取适当的k和ε,才能达到较好的控制效果。图3是滑模面和滑模运动的曲线图。当k=40,ε=5时,滑模面S=0以及系统到达滑模面和在面上的运动曲组线。

当系统加入脉冲扰动时,输出响应如图4所示。在0.3 s时加入扰动后,悬浮气隙和悬浮位置误差产生振荡,在0.1 s内又恢复稳定,具有很强的鲁棒性。
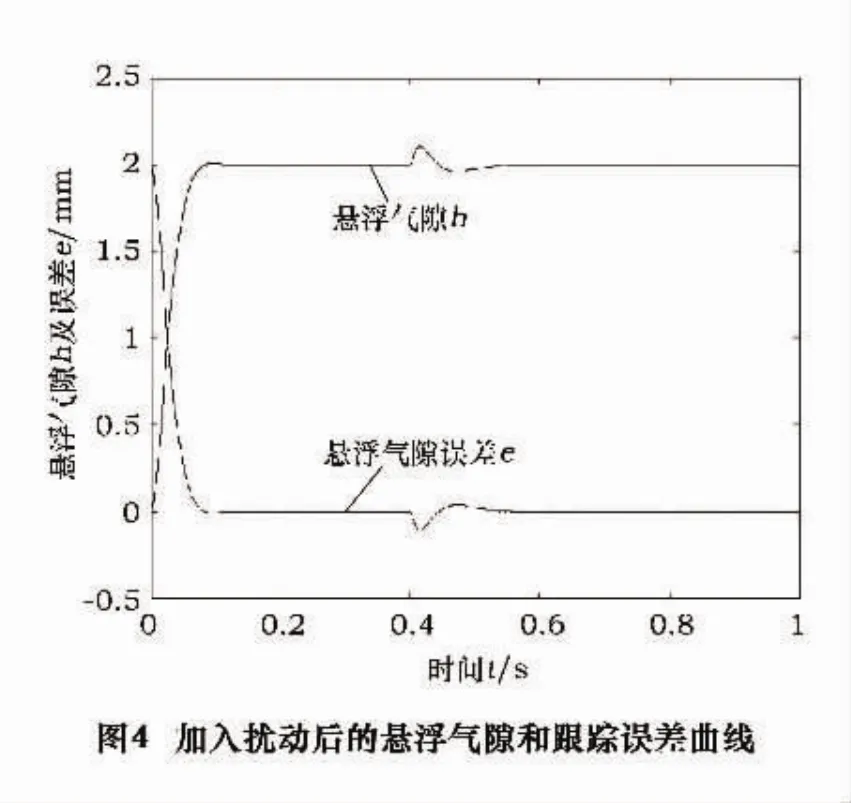
图5是磁悬浮系统加入了阶跃扰动后的输出曲线图。图5a的悬浮气隙在受到干扰后,气隙增加到2.18 mm左右,经过调节又回到期望值。电磁线圈电流增加到8 A,在1.25 s时稳定在7.33 A。
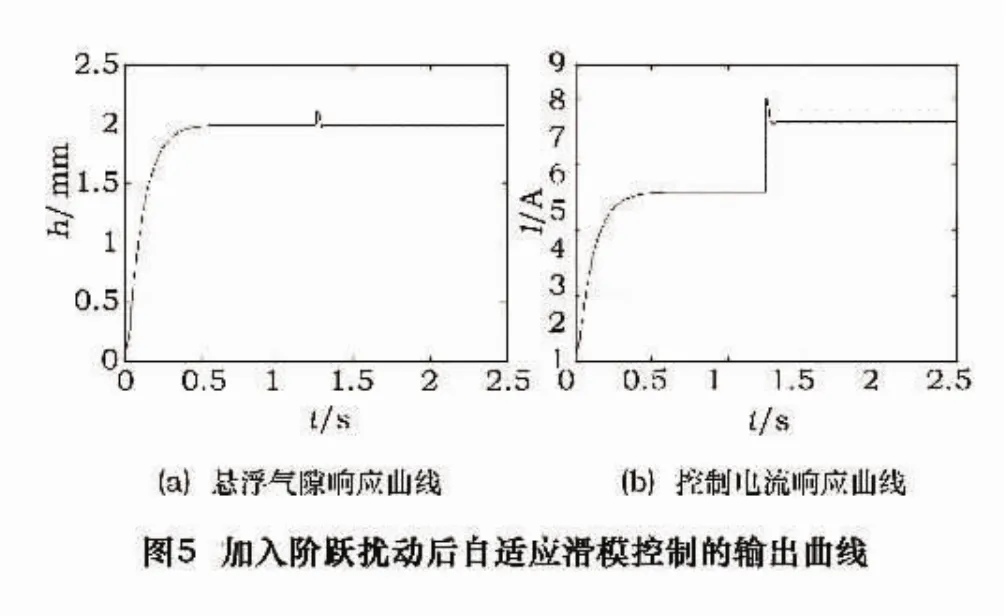
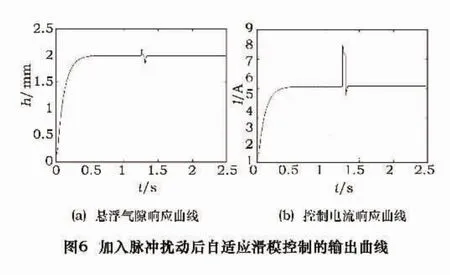
图6是磁悬浮系统加入脉冲扰动干扰后的悬浮气隙和电流的输出。图6a为悬浮气隙的输出,可以看到振荡很小,而且振荡后可以快速回到给定值。图6b为控制电流的输出曲线图,控制电流的振荡稍大,但是也能快速回到给定的参数值。
滑模变结构控制可保证系统稳定,是一种鲁棒性强、稳定性好、超调小、响应速度快的控制方法。滑模控制对被控对象的数学模型不作精确的要求,在一定的范围内参数的摄动不会给系统带来影响,并能有效的抑制外加干扰。
4 结语
本文在龙门移动式数控加工中心中引入了磁悬浮技术,彻底消除了摩擦,并采用了基于反馈线性化的自适应滑模变结构控制方法对磁悬浮系统进行控制。但由于系统的动态模型,在其运行过程中会产生扰动,为克服这些问题,使用∞控制理论结合积分型滑模控制器的设计方式来加强控制器的鲁棒性,并再利用自适应控制理论来估测控制器参数,以减缓系统抖动情形的发生。实验结果表明与传统的状态反馈方法相比,无超调,响应速度快且能够有效地抑制干扰。系统的参数变化以及添加的外部扰动对输出的影响不大,即系统具有较强的鲁棒性。
1 杨霞,李强,郭庆鼎.基于数控机床进给用磁悬浮直线电机摩擦的消除[J].组合机床与自动化加工技术,2005(7)
2 Jinunshian Phuah,Jianming Lu.Chattering Free Sliding Mode Control in Magnetic Levitation System[J].IEEJ Trans EIS,2005,125(4)
3 王丽梅,石佳.基于反馈线性化的龙门数控机床磁悬浮系统滑模鲁棒控制[J].机床与液压,2008,36(5)
4 王军闯.NC机床磁悬浮进给机构研究[D].大连交通大学.2006.
5 F.Castanos,L.Fridman.Analysis and design of integral sliding manifolds for systems with unmatched perturbation[sJ].IEEE Trans.Automatic Control,Vol.51,no.5,pp.853 -858,May 2006.
6 [美]斯洛廷 J-JE,李卫平.应用非线性控制[M].北京:机械工业出版社,2004.
7 王丽梅,石佳.龙门移动式数控机床横梁磁悬浮控制系统研究[J].制造技术与机床,2008(2)
8 Z.J.Yang,M.Minashima.Robust nonlinear control of a feedback linearable voltage - controlled magnetic levitation system[J].Trans.IEEJapan,2005,121(7)
9 梅生伟,申铁龙,刘康志.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2003.
10 P.Tsiotras and M.Arcak.Low -bias control of AMB subject to voltage saturation:state-feedback and observer design[sJ].IEEE Trans.Control Systems Technology,vol.13,no.2,pp.262 -273,Mar.2005.
11 刘金琨.滑模变结构控制MATLAB仿真[M].清华大学出版社,2005.
如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。
Sliding Mode-H∞Control of Magnetic Levitation Used in Gantry Machining Center
LIU Chunfang,AN Mingwei,WANG Limei
(School of Electrical Engineering,Shenyang University of Technology,Shenyang 110023,CHN)
The levitation rigidity of gantry NC machine tool was studied.The magnetic levitation technology is adopted for the moving crossbeam of the gantry NC machine tool in order to eliminate friction and increase machining precision.Adaptive integral sliding mode controller with∞method is further proposed to achieve steady levitation.In this paper,the adaptive control is used to improve the chattering behavior.And the random disturbance can be suppressed by the control with∞method.Finally,the experimental result shows this system has powerful ability of suppressing disturbance and high rigidity.It can achieve steady levitation.
Magnetic Levitation System;Feedback Linearization;Sliding Mode Variable Structure Control;Adaptive Control
TP273
A
* 国家自然科学基金项目(50805098)
刘春芳,1975年生,女,副教授,博士,从事伺服系统、鲁棒控制及计算机仿真等方面的教学、科研工作。
p
2009-07-14)
10125

