链-索-链型悬链锚泊线静力问题的若干算式

于 洋

(浙江海洋学院,舟山 316000)

链-索-链型悬链锚泊线静力问题的若干算式

于 洋

(浙江海洋学院,舟山 316000)

在无流速、忽略拉伸变形的假定条件下,对链-索-链型悬链锚泊线的静力问题进行了理论研究。以隐函数方程的形式给出了海底锚链离底部分长度的计算式,以参数方程的形式给出了悬链线形状及张力的解析解,所有结果均为无因次表达式。

悬链线;锚泊;静力特性;解析解

Abstract:A theoretical study on the static performance of catenary chain-wire-chain mooring line is carried out in this paper based on the assumption condition that there is no current and deformation of the line is neglected.The length of the chain cable that is hauled up from seabed is determined by an implicit equation,the coordinates and tensions at each points of the catenary line are of analytical solutions described by parametric equations.All of the results are shown in non-dimensional type.

Key words:catenary line;mooring;static performance;analytical solution

0 前言

中等水深条件下的海洋浮体定位,常采用链-索-链锚泊系统,利用悬链线特性为浮体提供恢复力[1]。该锚泊线主要由锚链和钢索组成,在海底锚桩一端和水面浮体一端分别采用一段锚链,锚链之间由钢缆连接。在锚泊线上有的安装沉子或浮子以改善锚泊性能[2]。锚或锚桩只承受水平作用力,因而要求海底锚链在锚(桩)处要与地面保持相切。对于这种复合锚泊线,一般采用数值方法进行静力计算,并需考虑水流作用和锚泊线拉伸变形的影响[3～5]。然而,在无流、无浮子或沉子条件下,如忽略锚泊线拉伸变形,则可以得到其静力问题的理论解——以隐函数方程和解析解的形式给出其计算公式。

1 悬链线基本公式

假定无流速,海底平坦,且忽略锚泊线拉伸变形(单一类型锚链线如图1所示),将坐标系 XOZ的原点O取在锚链悬链线与海底的切点处,则悬链线上距原点长度L的点的坐标可写为[6,7]

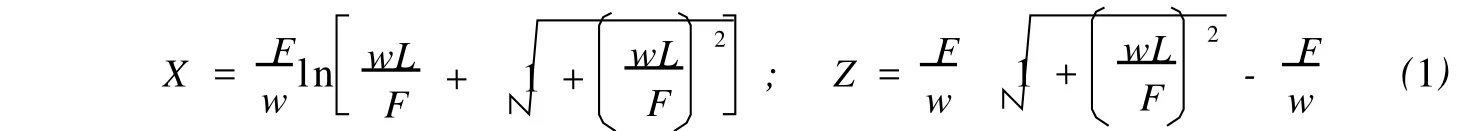
可见,该坐标满足以L为参变量的参数方程。当悬链线上距原点长度L0时,Z=H,有

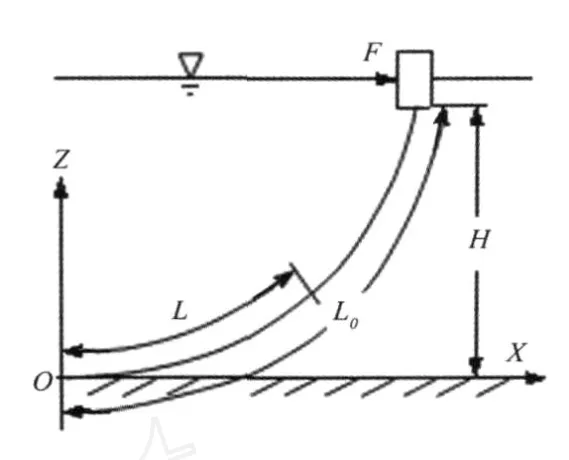
图1 单一锚泊线示意图

式(1～2)中:w为水中锚泊线单位长度重量;F为水平外力;L0为悬链线长度。

2 链-索-链型锚泊线海底锚链离底部分的长度

图2所示的整个锚泊线由L1、L2和L3段组成,其中L1和L3段为锚链;L2段为钢索。L4为海底锚链被拉起的长度。为求解出L4,分别将L1段和L2段按照悬链线形状延长直至与水平线相切(图中虚线部分)。L1段延长长度记为L1′;L2段延长长度记为 L2′。在三个切点处分别建立坐标系 XOZ、X′O′Z′和X"O"Z"。于是 ,利用式(2),并结合图 2,有

图2 组合锚泊线及其局部延长线

另外 ,对 L1′段和(L2+L2′)段、L3段与 L2′段进行受力分析 ,可得

上面各式中:w1、w2和 w3分别为L1、L2和L3段锚泊线在水中的单位长度重量。

现对上面各参数作无因次化,令

对于一个具体锚泊线来讲,上式中 n1、n3、l1和l2均为已知量,所以式(9)就是关于 l4的隐函数方程。给定某一外力 f后,可利用式(9)数值求解出 l4。当 n1=n3=1时,该式则退化为普通的悬链线方程。

如果令 l4=0,n3=1,则式(9)变为

将式(7)代入式(3)、(4),连同式(5)一起代入式(6),并进行无因次化,化简后可得到:

利用该方程可求出l3段锚链刚好完全卧底时的临界外力 fcr。如果实际外力 f

3 悬链线上各点坐标计算

因为整个锚泊线由三段悬链线组成,所以应先在各自的坐标系中求出其悬链线坐标,再通过坐标平移至同一个坐标系中。

3.1 三段悬垂线在各自坐标系中的参数方程

参照式(1),可得L4段在 XOZ坐标系中的悬链线方程:

3.2 坐标原点O′和O"在坐标系 XOZ中的坐标

利用L4段和L2′段纵、横长度之差,可以求出O′点在 XOZ坐标系中的坐标:

3.3 坐标系平移之后的悬链线坐标

首先将式(13)～式(16)平移至 XOZ坐标系中。考虑到原点O,即切点位置随外力大小而变,故随后再平移至以锚(桩)处为原点的坐标系中(仅横坐标改变)。为方便,横、纵坐标仍用 x、z表示。L1段平移后方程为

上面各式中,Δl如式(27),其中 ls2为外力小于临界力时,悬链线中钢索的长度,由式(10)确定。

4 悬链线各点张力

当外力 f大于临界力fc时,悬链线上各点无因次张力由式(28)、式(29)求出:

当外力 f小于临界力fc时,tx同式(28),tz由下式求出:

5 算例

设某悬链锚泊线的顶端锚链长L1=220 m;单位长度水中重量 w1=2 730 N/m;海底锚链长L3=400 m;单位长度水中重量 w3=2 340 N/m;中间钢索长L2=1 200 m;单位长度水中重量w2=780 N/m。锚泊线顶端距海底高度为 H=500 m。当锚泊线顶端索受水平外力F分别为1 000 kN和1 800 kN时,求悬垂线坐标及张力。

解:

步骤1:对各物理量进行无因次化

l1=L1/H=0.44;l2=L2/H=2.4;l3=L3/H=0.8;n1=w1/w2=3.5;n3=w3/w2=3.0;f1=F1/(w2H)=1 000 000/(780×500)=2.564;f2=F2/(w2H)=1 800 000/(780×500)=4.615。

步骤2:求出海底锚链刚好全部卧在海底时临界外力 fcr

此步骤作为下一步计算判断之用。因为海底锚链刚好全部卧在海底时,l4=0,故将 f视为未知量,由式(10)数值求解(本文采用二分法,步骤3与4的数值求解亦采用该方法),得 fcr=3.675。

步骤3:当外力 F=1 000 kN(f1=2.564)时的悬链线形状与张力

因为 f1

由于底部锚链全部卧底,故只需利用式(21)～式(24)计算悬垂部分钢索和顶部锚链的悬链线坐标。并注意在这4个式子中,l4=0,l2=1.9875。

悬链线张力由式(28)～式(31)计算,同样有 l4=0,l2=1.9875。

步骤4:当外力 F=1 800 kN(f2=4.615)时的悬链线形状与张力

因为 f2>fcr,故需由式(9)数值解出海底锚链被拉起的无因次长度,得l4=0.1077,实际长度为500×0.1077=53.85 m。悬链线总的无因次长度为l1+l2+l4=0.44+2.4+0.1077=2.9477,实际长度为500×2.9477=1 473.85 m。

因为 l4>0,所以悬链线坐标由式(21)～式(26)计算,悬链线中各点的张力运用式(28)～式(31)计算。

根据上述计算结果,将两种外力条件下的悬链线坐标绘于图3中,悬链线张力绘于图4中(均已换算成有因次物理量)。图4给出了锚链线张力沿着悬链线的变化情况,其横坐标表示悬链线长度,L=0对应的是锚链线与海底的切点;纵坐标为锚链线张力。在曲线中部,对应的是悬链线中钢索部分,由于单位长度重量较小,锚泊线张力增加趋势较缓;而在曲线右端部,对应的是顶端锚链,由于单位长度重量较大,锚链线张力快速增加。

6 结语

在无流速、锚泊线无拉伸变形的假定条件下,推导出了链-索-链悬链线静力特性的理论解。悬链线形状与张力以参数方程的形式给出了较为简单的解析解。在计算悬链线张力时,该参数为从悬链线与水平线切点起算的悬链线长度。在计算悬链线形状时,该参数亦为悬链线长度,但分为三部分,分别在图2所示的三个坐标系中单独定义,并没有随悬链线坐标平移而改变,故出现每一段悬链线长度l的取值范围不同的情况,即彼此不连续。但计算出的悬链线形状在连接点处是光滑、连续的。从物理意义上讲,这是由式(7)的力平衡关系所决定的。海底锚链被拉起的部分的长度,以隐函数方程的形式给出,具体计算时还需要采用数值方法。

[1] Ruinen I R M.The Use of Drag Embedment Anchors in Offshore Mooring Systems[J].Ingeokring Newsletter,2003,9(1):7-9.

[2] 王冬姣.索-链-浮子/沉子组合锚泊线的静力分析[J].中国海洋平台,2007,22(6):16-20.

[3] 潘斌,高捷.浮标系泊系统静力计算[J].重庆交通学院学报,1997,16(1):68-73.

[4] 滕斌,郝春玲,韩凌.Chebyshev多项式在锚链分析中的应用[J].中国工程科学,2005,7(1):21-26.

[5] 张火明,范菊,杨建民.深水系泊系统静力特性快速计算方法研究[J].船海工程,2007,36(2):64-68.

[6] 于洋,李伟.锚泊中船舶卧底链长的一种估算方法[J].中国航海,2002,1:40-42.

[7] 缪国平.挠性部件力学导论[M].上海:上海交通大学出版社,1995.

Solutions of Static Performance of A Catenary Chain-Wire-Chain Mooring Line

YU Yang
(Zhejiang Ocean University,Zhoushan 316000,China)

U675.922

A

1001-4500(2010)02-0006-05

2009-09-02; 修改稿收到日期:2010-01-15

浙江省科技计划重大项目资助(2008C03010)

于 洋(1963-),男,教授,从事船舶与海洋工程流体力学、航海技术研究。