基于ANN响应面法和Monte Carlo法的海洋平台可靠度分析

黄小光, 许金泉

(1.中国石油大学,东营 257061;2.上海交通大学,上海 200240)

基于ANN响应面法和Monte Carlo法的海洋平台可靠度分析

黄小光1,2, 许金泉2

(1.中国石油大学,东营 257061;2.上海交通大学,上海 200240)

利用人工神经网络(ANN)响应面法和Monte Carlo法对波流联合作用下固定式海洋平台进行了可靠度分析。综合考虑各种随机变量对海洋平台失效的影响,通过有限元方法获得一组随机变量和结构响应数据,利用BP神经网络模型构建平台结构的隐式功能函数。基于Monte Carlo方法由MATLAB软件产生大量的随机变量组合,通过统计网络映射结果确定结构的可靠性。

人工神经网络;Monte Carlo法;功能函数;可靠度

Abstract:Reliability analysis of fixed offshore platform subjected to wave and current is studied by response surface method of artificial neural network(ANN)and Monte Carlo simulation.The effects of different random variables to the invalidation of platform are synthetically considered,the structural response data and random variables are obtained by finite element methods.The BP neural networks are built to the implicit performance function of platform structure.Based on the Monte Carlo simulation,MA TLAB software generates lots of combinations of stochastic variables,by counting the mapping results of BP networks;the reliability of structure is obtained.

Key words:artificial neural network;Monte Carlo method;performance function;reliability

0 引言

海洋油气开发是一个高投入高风险的产业。海洋平台作为海洋资源开发的基础性设施,其安全可靠性对海洋油气生产和作业人员安全至关重要,因此海洋平台的可靠度评价一直是工程研究人员极为关注的问题。由于海洋平台工作环境的复杂性、恶劣性以及威胁平台安全因素的随机性,致使平台结构可靠度分析的功能函数难以显式表达,这限制了传统可靠度计算方法的应用。目前海洋平台可靠度的计算方法主要分三种:一是基于疲劳损伤理论的疲劳寿命可靠度分析,该方法通过有限元计算平台管节点的热点应力范围,应用疲劳累积损伤理论和S-N曲线对平台结构进行可靠度评估[1～4]。二是基于失效模式识别的平台系统可靠度分析,该方法通过计算失效模式的概率寻找系统的主要失效模式,用联合概率近似算法确定系统的可靠度[5,6]。三是通过规范确定平台结构的极限状态,采用Monte Carlo结合有限元法、响应面法等方法计算结构的可靠度[7,8]。第一、二种方法实现起来过程复杂,工作量较大,不易为广大工程技术人员所接受。第三种方法思路非常明确,但Monte Carlo结合有限元法需要过多抽样次数,不太适于大型复杂结构的可靠性分析,相对而言响应面法在大型结构的可靠性分析中的运用更为广泛。响应面法是用数值拟合构造一个函数代替功能函数进行可靠度分析,因此构造函数的拟合效果直接影响到可靠度计算结果。响应面法采用多项式拟合响应面,对于多参数非线性问题,响应面一般为多维非线性曲面,但多项式拟合的精度不够[7]。本文将人工神经网络与响应面法相结合,形成一种基于神经网络响应面法和Monte Carlo法的可靠度计算方法。该方法利用神经网络强大的非线性拟合功能构造结构响应面,能克服传统响应面法响应面拟合精度不足的弱点,对于海洋平台之类的大型复杂结构的可靠性分析具有一定的实用价值。

1 极限状态方程

1.1 确定基本变量及分布

确定描述结构状态的基本变量为 X1,X2,…,Xn。通常情况下,这些参数一般包括结构的几何形状尺寸、材料特性参数、载荷参数等,通过统计确定它们的分布状态。

1.2 选取结构抗力 R,建立极限状态方程

结构抗力指整个结构或构件承受内力或变形的能力。结构抗力可以看成基本变量的函数,即 R=R(X1,X2,…,Xn)。结构抗力一般根据工程需要选取,可以选取结构危险点的应力极限,也可以选取某些关键点的容许位移。结构作用效应S指由作用引起的结构的内力和变形(如内力、应力、位移等),可以表示为 S=S(X1,X2,…,Xn)。若以 X=(X1,X2,…,Xn)表示基本变量参数向量,则功能函数可写成:

当 g(x)>0时,表示结构安全,其发生概率 Pr就是结构的可靠度;当 g(X)<0时,表示结构失效;当 g(X)=0时,表示结构处于极限状态。根据上面定义结构可靠度的表达式可写成:

式中 P(·)表示括号内事件发生的概率。

2 BP神经网络模型

2.1 获取样本

根据统计结构合理选取或按随机抽样方法获得这些基本随机变量的m种组合,将它们作为m组予以输入。对各随机变量组合所确定的结构模型进行有限元分析,可得到对应的m组作用效应S,构成m组 X-S对。

2.2 建立BP神经网络模型

按照人工神经网络原理,建立BP网络模型。将m组基本变量作为网络的输入,输入层包括 n个节点,对应基本变量个数;其输出层节点数由结构抗力确定,这里取一个节点。然后随机将上述 m组 X-S对中的一部分作为BP网络的训练样本,训练完毕之后,用 X-S对中余下的部分对网络进行测试。

3 Monte Carlo方法计算可靠度

如果网络测试结果合理,即可用Monte Carlo仿真方法求解结构的作用效应和可靠度。根据基本变量的分布规律由MATLAB产生L组随机抽样组合,将随机抽样组合作为BP网络的输入,对网络激活,得到结构相应的作用效应S,再与结构抗力R进行比较。若R>S,则表示结构处于安全状态;反之则表示结构失效。如此重复进行L次,统计L次网络仿真后结构处于安全状态的次数M。由大数定律知,当仿真次数L足够大时,频数M/L就近似等于结构的可靠度。

4 算例

4.1 结构有限元模型

本文通过研究波流联合作用下固定式海洋平台的可靠度来验证方法的高效性和正确性。平台类型为导管架平台,由上层平台结构和下部的导管架结构组成,导管架底部通过桩基础固定。平台高98 m,所在水域深80 m,底部轮廓为正六边形,面积约为235 m2。上层平台结构包括两层矩形甲板(厚0.02 m)和支撑框架(矩形,0.2 m×0.3 m)。下部导管架由一系列钢管焊接而成,主体是6根主导管(Φ1.2 m×0.03 m),其间用细管件(Φ0.5 m×0.02 m)为支撑,组成空间塔架结构。利用有限元软件ANSYS建立固定式海洋平台的有限元模型,如图1所示。采用PIPE59单元模拟泥面以上至导管架帽以下的支撑结构;采用PIPE16单元模拟泥面以下部分结构;采用BEAM4单元模拟甲板的框架梁,SHELL60单元模拟甲板。模型共有1 793个节点,2 337个单元。为简化计算,借鉴“等效桩法”取桩基在土壤以下6 m处(相当桩基外径5倍)固支。平台结构分析的载荷主要包括海流载荷、波浪载荷、结构自重载荷等,自重载荷由程序按单元截面积和长度自动生成并施加;海流载荷、波浪载荷利用了ANSYS提供的PIL E 59单元的流体动载荷自动生成功能施加。考虑结构的运动,ANSYS程序关于水动力载荷按结构与流体的相对运动速度表示的Morison方程为式中:{f}为流体动力效应引起的单位长度的载荷;CD为法向曳力系数;CM为法向惯性力系数;CT为切向曳力系数;{˙un}为法向流体质点相对速度矢量;{˙vn}为法向流体质点加速度矢量;{˙ut}为切向流体质点相对速度矢量,以上流体质点速度均为波浪速度与海流速度的矢量和;De为考虑附着层厚度的外径值;ρw为海水密度。

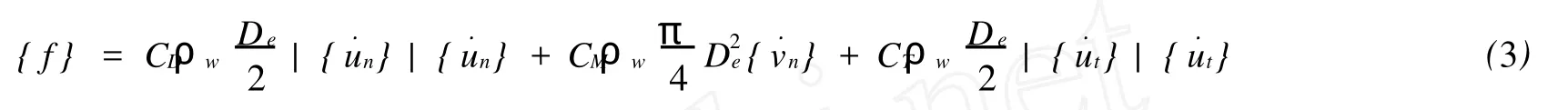
通过ANSYS软件的波流参数表填写对应的参数值,包括波浪理论选项、波流相互作用选项、水深、海水密度、波浪入射角、流速、流向、波高、波峰相位角和波周期等,软件自动生成流体载荷并施加到平台结构上,以保证计算进行。

4.2 结构极限状态方程

首先考虑以平台甲板的最大水平位移Dmax为可靠性控制目标。影响Dmax的变量非常多,本文选取波浪周期、波高、波浪相位角、入射角、海流速度、流向及主导管尺寸等为基本变量。目前一些文献计算波流共同作用的海洋结构物可靠度时,往往忽略波流入射角及波浪相位角的影响,采用任意选取波流方向或由相位搜索确定对结构作用力最大的相位角进行计算。由于海洋环境的复杂性,波流不可能一直沿一个方向作用到平台上,而波浪相位角也是随机的,这样得到的结论欠准确。由于没有统计数据,于此把波浪相位角处理成[0°～360°]均匀分布。波浪及海流方向主要受风向影响,西南和东北风向偏多,于此将波浪海流方向分两个阶段的正态分布,由于结构对称性,即可只需考虑其中一种情况。各基本变量统计特征如表1所示。

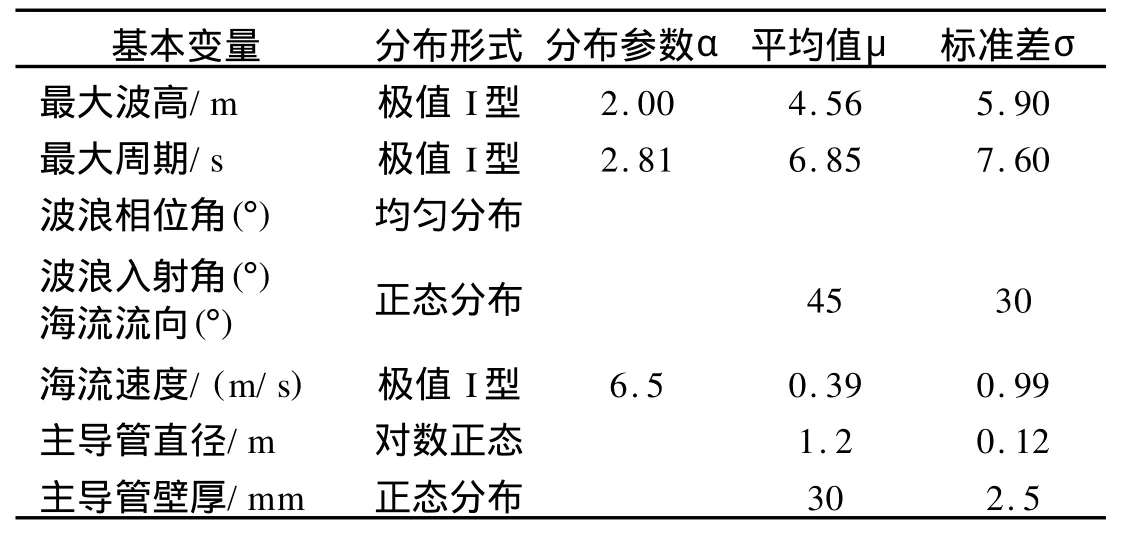
表1 基本随机变量统计特征表

显然平台甲板的最大水平位移Dmax随基本变量而变化。可把Dmax看成以上七个基本变量的函数,则平台的功能函数可以表示为

式中:Du表示极限状态下平台甲板的最大水平位移;x1…x7分布对应表1中的七个基本随机变量。

4.3 网络训练与测试

参考已有的波浪数据[13],合理选取其他基本变量,产生一系列基本变量组合,分别对这些变量组合确定的结构进行有限元分析,计算平台甲板的最大水平位移 Dmax。有限元数据样本如表2所示,这组样本可以用来训练及测试神经网络。

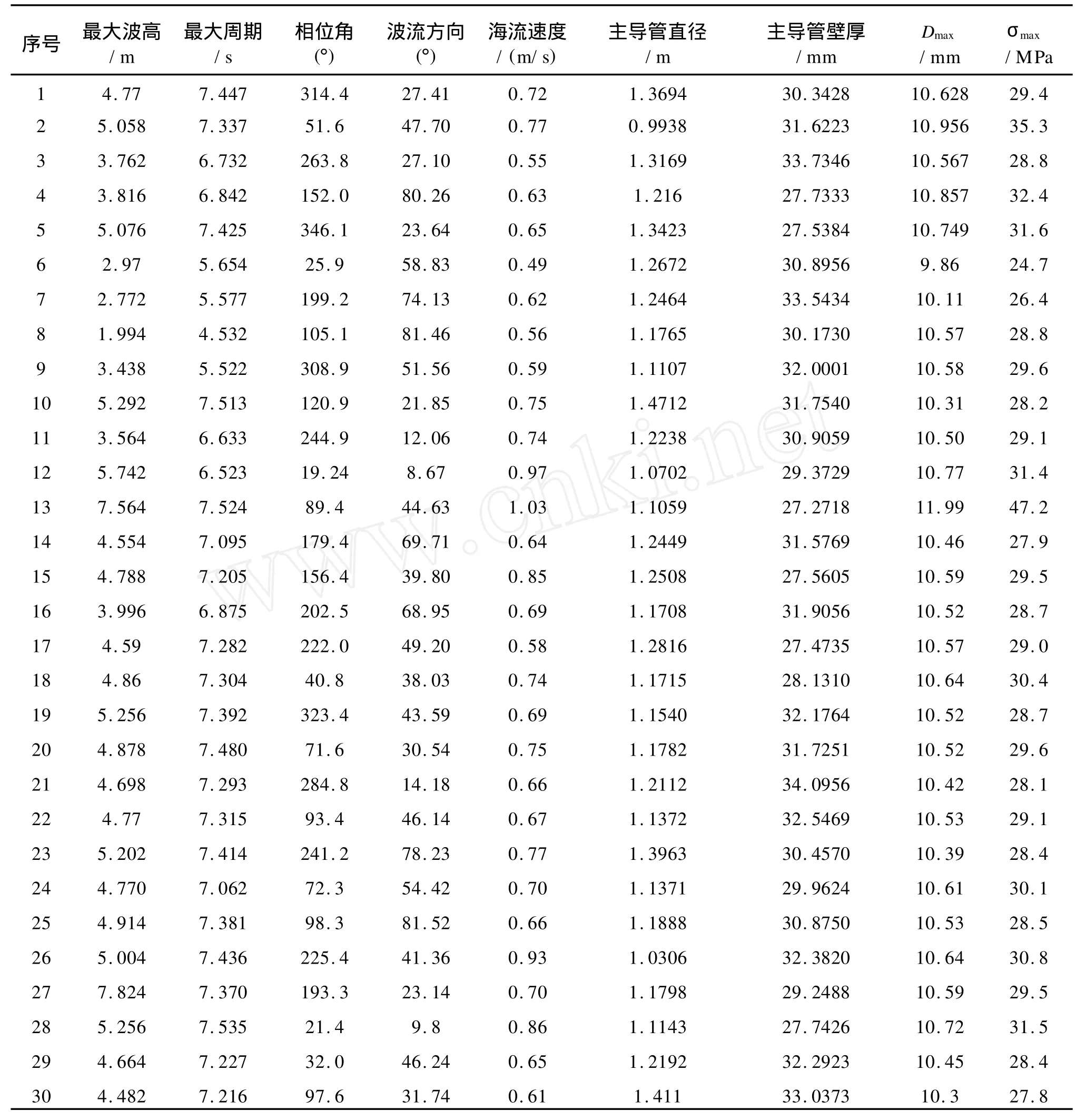
表2 有限元数据样本

建立BP神经网络模型,以随机变量 x1,x2,…,x7作为网络的输入参数,Dmax作为网络的输出参数,并对输入输出参数进行归一化处理;隐含层的传递函数选用tansig函数,输出层的传递函数选用logsig函数;网络的训练目标误差为 E=10-6,学习率为0.35;网络输入层、隐含层和输出层的神经元数目分别为7、15、1。将前25个有限元数据样本作为BP网络的训练样本,调用MATLAB神经网络工具箱对该BP网络进行训练,网络经3 283次迭代后收敛,得到训练好的网络。将后5个有限元数据样本代入训练好的BP网络,对网络进行测试,测试结果如表3所示。通过测试可以看到,该网络模型可以较好地描述上述七个随机变量与甲板最大水平位移之间的关系,由该模型所确定的结构响应面法比传统响应面法在精度上提高了。

同时测试结果也直观地说明了神经网络的预测功能,利用这个网络模型可以很方便地预测各种海况下平台甲板的最大水平位移,如需要更好地预测精度,可再增加训练样本的数量。

4.4 仿真结果

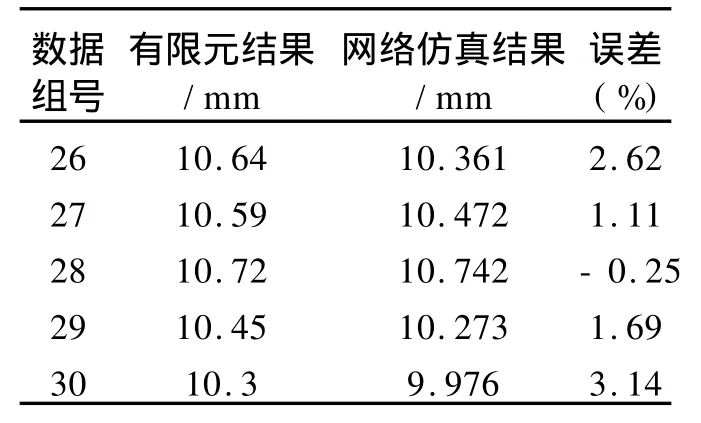
表3 BP网络测试结果

由上述模型,通过MATLAB平台实现Monte Carlo仿真计算海洋平台的可靠度。参照工业与民用建筑高层钢结构规范,平台正常使用时,顶端水平位移与高度之比值下限为1/500,所以本文平台的 Du取200 mm,对导管架平台进行可靠性分析。利用MATLAB产生以上七个基本变量满足如表1分布规律的随机组合样本,将这些样本作为网络的输入,激活网络得到相应的仿真结果。统计仿真结果发现,仿真结果大于200 mm(平台处于失效状况)的概率几乎为零,仿真结果大于50 mm的概率小于0.001%。因此不以平台最大水平位移作为可靠度的控制目标,改用平台最大应力为可靠度控制目标。平台用钢的屈服极限σs=234 MPa,极限应力取为σu=117 MPa,建立相应的功能函数,应用同样步骤计算平台可靠度,表4显示了可靠度随抽样样本组合数的变化情况。

表4 仿真结果

从表4可以看出,网络仿真20 000次已能得到足够精确的结果,而计算仅用时5 min,这充分说明本文方法的效率之高。本文方法的另一优点是不受随机变量数目及随机变量分布规律的影响,MATLAB软件可以产生常见的所有随机变量分布。大型软件如ANSYS也有可靠度分析模块,但软件提供的随机变量分布种类很少,且工程很常见的极值型分布甚至没有,致使ANSYS之类软件可靠度计算的推广受到限制。另外,在结构的某些参数或基本变量的分布规律发生变化时,本文方法可以不需要重新进行有限元计算和网络的重新训练,直接用原网络模型进行仿真即可。

5 结论

本文通过对固定式海洋平台的可靠性分析,说明基于ANN响应面法和Monte Carlo方法的可靠度分析的可行性。借助神经网络的高度非线性映射关系能力和Monte Carlo法随机抽样的思路,利用MATLAB强大的数值计算功能,对大范围的数据进行概率分析,求出结构系统的可靠度。本文方法能够克服复杂结构可靠度计算中极限状态方程无法显式表达的困难,而且不受随机变量个数及其分布规律的影响。与传统的结构可靠度计算方法相比,本文方法仅需少量分布合理的有限元计算结果,工作量降低,对于大型复杂结构优势非常明显。

[1] 张立,金伟良.海洋平台结构疲劳损伤与寿命预测方法[J].浙江大学学报(工学版),2002,36(2):138-142.

[2] 陈伯真,胡毓仁,严庆谊.海洋平台关节点的疲劳可靠性分析[J].中国海洋平台,1996,11(3):114-117.

[3] 许亮斌,陈国明.考虑疲劳失效的海洋平台动态可靠性分析[J].石油学报,2007,28(3):131-134.

[4] Madhavan Pillai,et al.Fatigue reliability analysis of fixed offshore structure:A first passage problem approach[J].浙江大学学报A(英文版),2006,7(11):1839-1845.

[5] 胡云昌,刘闯,余建星,郭振邦.导管架平台的三维可靠度分析[J].海洋学报(中文版),1995,17(6):117-125.

[6] 杨国安,盖会明.海洋平台水下结构累积损伤失效路径的动态搜寻方法[J].中国海洋平台,2006,21(6):12-17.

[7] 桂劲松.结构可靠度分析的改进BP神经网络响应面法[J].应用力学学报,2005,22(1):127-130.

[8] 张崎,李兴斯.海上导管架平台可靠性分析抽样-模拟方法[J].大连理工大学学报,2006,46(2):166-169.

[9] 李茜,杨树耕.采用ANSYS程序的自升式平台结构有限元动力分析[J].中国海洋平台,2003,18(4):41-46

[10] 杨树耕,藤明清等.有限元分析软件ANSYS在海洋工程中的应用(续1)——第二讲采用ANSYS程序[J].中国海洋平台,2000,15(5):40-46.

[11] 桂劲松,康海贵.结构可靠度分析的响应面法及其Matlab实现[J].计算力学学报,2004,21(6):683-687.

[12] 安伟光,蔡荫林,陈卫东.随机结构系统可靠度分析与优化[M].哈尔滨:哈尔滨工程大学出版社,2007.

[13] 沈照伟.基于可靠度的海洋工程随机载荷组合及设计方法研究[D].杭州:浙江大学,2004.

[14] 纪冬梅,胡毓仁.结构疲劳寿命及可靠度的神经网络预测方法[J].上海交通大学学报,2005,39(2):256-259.

[15] 焦李成.神经网络系统理论——智能科学与非线性科学丛书[M].西安:西安电子科技大学出版社,1990.

[16] 王正林,龚纯,何倩.精通MATLAB科学计算[M].北京:电子工业出版社,2007.

Reliability Analysis of Offshore Platform Based on Response Surface Method of ANNand Monte Carlo Simulation

HUANG Xiao-guang1,2, XU Jin-quan2
(1.China University of Petroleum,Dongying 257061,China;2.Shanghai Jiao Tong University,Shanghai 200240,China)

P75

A

1001-4500(2010)02-0045-05

2009-07-21; 修改稿收到日期:2010-01-16

黄小光(1980-),男,讲师,博士研究生,从事石油管线结构力学分析、海洋石油钻采设备的疲劳可靠性分析工作。