THE FORM INVARIANCES AND THE HOJMAN CONSERVED QUANTITIES FOR HAMILTON SYSTEMS*

Zhang Hong-Bin（张宏彬），Gu Shu-Long（顾书龙）and Chen Hai-Bo(陈海波)

（Department of Physics,Chaohu College,ChaohuAnhui238000）

THE FORM INVARIANCES AND THE HOJMAN CONSERVED QUANTITIES FOR HAMILTON SYSTEMS*

Zhang Hong-Bin（张宏彬），Gu Shu-Long（顾书龙）and Chen Hai-Bo(陈海波)

（Department of Physics,Chaohu College,ChaohuAnhui238000）

Abstract:The form invariance and the Lie symmetry are defined for Hamilton systems.A relation between the form invariance and the Lie symmetry is derived.The Hojman conserved quantity is constructed by using the generators of Lie symmetry.An approach to find Hojman conserved quantities in terms of the form invariance is presented.An example is given to illustrate the application of the results.

Key words:Hamilton system；form invariance；Lie symmetry；Hojman conserved quantity；PACC:0320

1 Introduction

The symmetry of mechanical systems is one of the most important subjects in physics,which has been investigated for a long time.The symmetry of a mechanical system will be useful for integrating the equations of motion,since it is closed related to invariants(or first integrals)of this system.The modern approaches of finding invariants are mainly in terms of the Noether symmetry,the Lie symmetry and the Mei form invariance.The Noether symmetry is an invariance of the Hamilton action under the infinitesimal transformation of a continuous group[1].The Noether′s theorem associates one conserved quantity to each Noether symmetry.The Mei′s form invariance is an invariance of dynamical functions of system such as Lagrangian,Hamilton,non-potential generalized force and generalized constrained force etc,under the infinitesimal transformation[2-6].A new conserved quantity can be obtained by using Mei′s from invariance[7]. Lie′s method consists in finding the continuous symmetry transformations that leave a system of differential equations invariant.These symmetry transformations constitute a Lie group.Once you have obtained the symmetry group,there are some ways to find first integrals.In 1979 Lutzky[8]showed that constants of motion for a Lagrangian system are determined even by point symmetries which do not preserve the action, and demonstrated that the explicit form of these conserved quantities can be specified from a knowledge of the symmetry group generator.In 2003,Fu and Chen[9]studied non-Noether symmetries and conserved quantities of nonconservative dynamical systems.

In 1992,Hojman[10]presented a new conservation law without using either Lagrangian or Hamilton,solely based on the existence of symmetries.This direct method has attracted much attention[11-18].In this paper,we study Hojman conserved quantities by using the Mei form invariance for the Hamilton systems.In section 2,the definitions of the form invariance and Lie symmetry are given.In section 3,the Hojman conserved quantity is constructed by using the generators of Lie symmetry for the Hamilton system.The relation between form invariance and Lie symmetry is deduced in section 4.A approach to find Hojman conserved quantities in terms of the form invariance is presented in section 5.Finally,a example is given to illustrate the application of the results.

2 Definition and criterion of form invariance for Hamilton systems

If the differential equations of motion of a mechanical system can be written in the form

then such system is called a Lagrangian system.The Lagrangian systems include(but not limited to): holonomic conservative system,holonomic system with generalized forces derived from a generalized potential,systems of inverse problem of Lagrange mechanics[19-20],nonholonomic systems with the equations of motion of the corresponding to the holonomic system governed by Eq.（1）,the Chaplygin systems with the Helmholtz potential[21-22]，the nonholonomic potential systems whose free motion can be realized[23].

Introducing the generalized momentums and the Hamilton

then Eq.(1)may be written in the canonical form

whereis the Hamilton.

Introduce the infinitesimal transformations with respect to time,generalized coordinates and generalized momentums

or their expansion formula

where ε is an infinitesimal parameter,τ（t，q，p）,ξs（t，q，p）and ηs（t，q，p）are called infinitesimal g enerators.Under the infinitesimal transformations（5）,Hamilton H（t，q，p）becomes H（t*，q*，p*）.

Definition 1:Under the infinitesimal transformation（5）,if the canonical equations（3）keep their form invariant,i.e.,

where

then such invariance is called a form invariance of the Hamilton systems.

Introduce the differential operator of the infinitesimal generators

and its extensions

Expanding H*,one has

From Eqs.(6)—(10),the following criterion can be obtained.

Criterion 1:The infinitesimal transformation（5）is a Mei's symmetric transformation of the system（3）,if and only if the infinitesimal generators τ（t，q，p）,ξk（t，q，p）and ηk（t，q，p）satisfy the following conditions

Proof:Substituting Eq.（10）into Eqs.（6）,using Eqs.（3）,and neglecting and the higher infinitesimal terms,Eqs.（11）will be obtained.

3 .The Hojman conserved quantity for Hamilton systems

The basic idea of the Lie symmetry is to keep the equations of motion（3）invariant under the infinitesimal transformations（5）.For convenience,Eqs.（3）are rewritten in following form

where gs=∂H/∂psand hs=-∂H/∂q· s.

Definition 2:The infinitesimal transformation（5）is a Lie′s symmetric transformationof the system（3）,if and only if there exist functionsτ（t，q，p）,ξs（t，q，p）and ηs（t，q，p）that satisfy the following determining equations

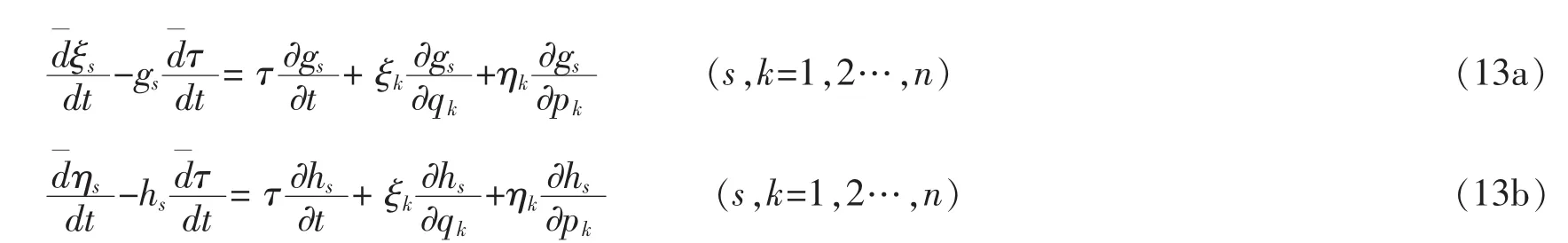
where

In terms of the generators of the Lie symmetry for equations（3）,the following theorem concerning conserved quantities can be proved.

Theorem 1:The system（3）possesses the following conserved quantuty

If the infinitesimal generators τ（t，q，p）,ξs（t，q，p）and ηs（t，q，p）satisfy the determining equations（13）,

and the function μ（t，q，p）admits the following equation

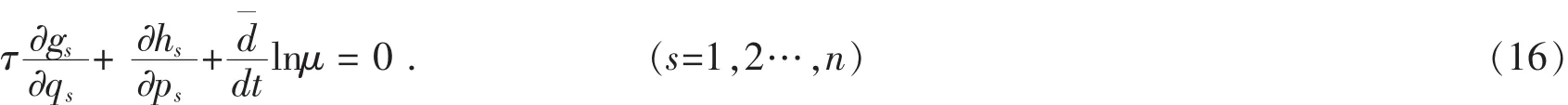
Proof:From Eq.（15）,one has

It is straightforward to show that for any function A（t，q，p）[10]

and substituting Eqs.（18）into Eq.（17）and using Eqs.（13），we obtain

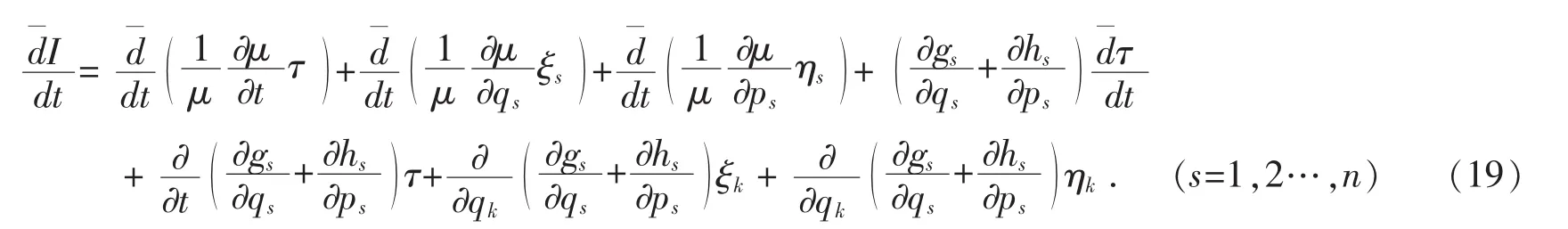
Finding the partial differential of Eq.（16）with respect to t，qkand pkrespectively,and substituting the results into Eq.（19），and using Eqs.（13），one can get

By virture of above theorem,one can easily dudece following corollaries：

Corollary 1：The system（3）possesses the following conserved quantity

if the infintesimal generators τ（t，q，p）=0,ξs（t，q，p）and ηs（t，q，p）satisfy（22）

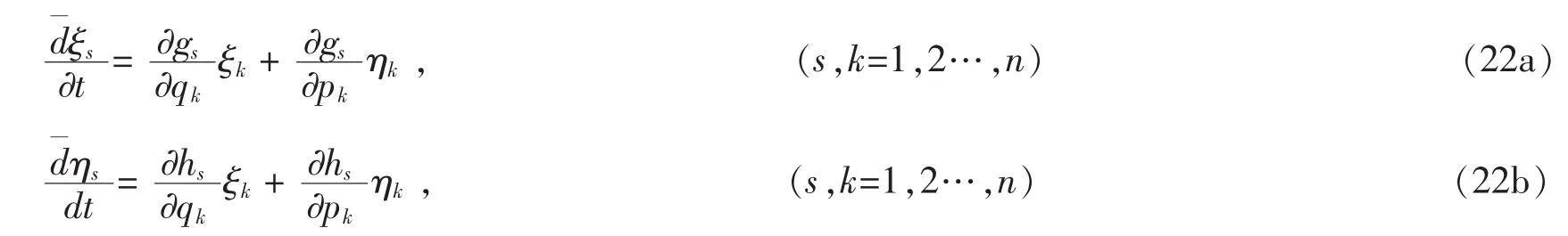
and function admits the equation（16）.This is the result of the literature[14].

Corollary 2：The system（4）possesses the following conserved quantity

If the infintesimal generators ξs（t，q，p）=0,τ（t，q，p）and ηs（t，q，p）satisfy（24）

and function μ=μ（t，q，p）admits the equation（16）.

Corollary 3：The system（4）possesses the following conserved quantity：

If the infinitesimal generators ηs（t，q，p）=0，τ（t，q，p）and ξs（t，q，p）satisfy（26）

and function μ=μ（t，q，p）admits the equation（16）.

4 Necessary and sufficient condition under which the form invariance is a Lie symmetry

From the deductions of Eqs.（11）and（13）,it can be seen that the form invariance is generally different from the Lie symmetry.For seeking their relations,the equation（3）may be rewritten as follows:

Then for the system（3）,the determining equations of a Lie's symmetry have new form

Some direction calculations yield

Equatio（29）demonstrates the relation between the form invariance and the Lie symmetry.From the relation, the following proposition can be derived.

Proposition 1:For the Hamilton system,the necessary and sufficient condition under which the form invariance is a Lie symmetry is that the following relations hold

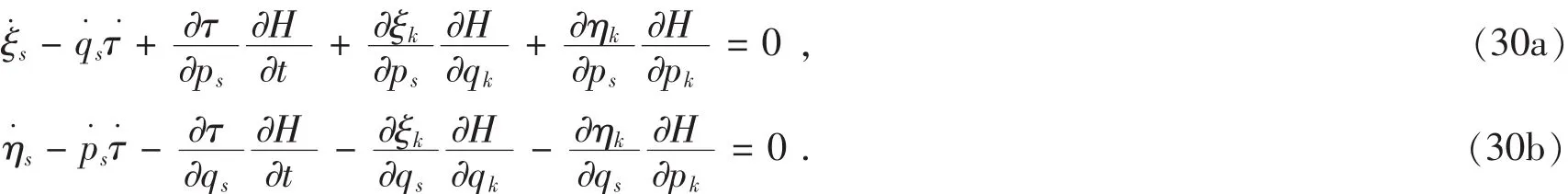
Let the sum of the coefficient of the terms which dependent on orrespectively equals zero,and the sum of the remainder of terms equals also zero,one has

Proof:Substitution of Eqs.（11）and（30）into Eq.（29）leads to X（1）（F）＝0 and X（1）（G）＝0. According to the determining equations（28）,we know that the form invariance is a Lie symmetry.

Particularly,if τ＝0,then the conditions（30）become

5 Hojman conserved quantity deduced from form invariance

The Hojman conserved quantity can be located by using the form invariance.

Proposition 2:For the Hamilton system,under the infinitesimal transformation（5）,if the infinitesimal generators τ（t，q，p），ξs（t，q，p）and ηs（t，q，p）satisfy Eqs.（11）and（30）,and there exists a function μ= μ（t，q，p）admits the equation（16）,then form invariance leads to the Hojman conserved quantity（15）.

Proof:If the infinitesimal generators τ（t，q，p），ξs（t，q，p）and ηs（t，q，p）satisfy Eqs.（11）and Eqs.（30）,by using proposition 1,we know that the generators are also Lie symmetrical.And we can subsequently obtain the conserved quantity（15）by using the theorem 1.

Proposition 3:For the Hamilton system,under the infinitesimal transformation(5),if the infinitesimal generators τ（t，q，p），ξs（t，q，p）and ηs（t，q，p）satisfy Eqs.（11）and（32）,and there exists a function μ=μ（t，q，p）admits the equation（16）,then form invariance leads to the Hojman conserved quantity（21）.

Proof:If the infinitesimal generators τ（t，q，p），ξs（t，q，p）and ηs（t，q，p）satisfy Eqs.（11）and（32）, proposition 1 means that the generators are also Lie symmetrical.Corollary 1 yields subsequently the conserved quantity（21）.

6 An Illustrative example

As an illustration of the theory developed in the preceding sections,consider the case of a simple degree of freedom linear damped oscillator

First,transform Eq.（33）into a Hamilton system,and its Lagrangian is

Therefore

Eq.（11）leads to

It can be easily verified that

are two solution sets of Eq.（36）.Since the generator（37）satisfies the Eq.（13）,so it is also the Lie symmetry of the system（34）.However,the generators（38）don’t satisfy the Eq.(13),so it isn’t the Lie symmetry of the system（34）.From Eq.（16）,one has

Equation（39）exists a solution

Inserting Eqs.(37)and(40)into Eq.(25)leads to conserved quantity

7 Conclusions

For Hamilton systems,we present an approach to find Hojman conserved quantities in terms of the form invariance.

Acknowledgments:The research supported by the National Natural Science Foundation of China under Grant No.10872037 and the National Natural Science Foundation of Anhui Province under Grant No. 070416226.

[1]Noether A E 1918 Nachr.Ges.Wiss.G·ttingen.Math.Phys.KI II 235

[2]Mei F X 2000 J.Beijing Inst.Technol.9 120

[3]Mei F X 2001 Chin.Phys.10 177

[4]Mei F X and Chen X W 2001 Beijing Inst.Technol.10 138

[5]Wang S Y and Mei F X 2001 Chin.Phys.10 373

[6]Wang S Y and Mei F X 2002 Chin.Phys.11 5

[7]Mei F X 2004 J.Dyna.Contrl.2 28.(in Chinese)

[8]Lutzky M 1979 Phys.Lett.72A 86

[9]Fu J L and Chen L Q 2003 Phys.Lett.317A 255

[10]Hojman S A 1992 J.Phys.A:Math.Gen.25 L291

[11]Gonález-Gascón F 1994 J.Phys.A:Math.Gen.27 L59

[12]Lutzky M 1995 J.Phys.A:Math.Gen.28 L637

[13]Pillay T and Leach P G L 1996 J.Phys.A:Math.Gen.29 6999

[14]Mei F X 2002 Chin.Sci.Bull.47 1544

[15]Mei F X 2003 Acta Phys.Sin.52 1048（in Chinese）

[16]Zhang H B,Chen L Q and Gu S L 2004 Acta.Mech.Sinica.36 254（in Chinese）

[17]Zhang H B,Chen L Q and Gu S L 2004 Commun.Thero.Phys.42 321

[18]Zhang H B and Chen L Q 2005 J.Phys.Soc.Jap.74（3）905

[19]Santilli R M 1978 Foundations of theoretical mechanics I.（New York:Springer-Verlag）

[20]Mei F X 1988 Special problems in analytical mechanics.（Beijing:Beijing institute of technology Press）（in Chinese）

[21]Novoselov V S 1966 Variational methods in mechanics.（Leningard:LGU）.（in Russian）

[22]Mei F X 1985 Foundations of mechanics of nonholonomic systems.（Beijing:Beijing institute of technology Press）（in Chinese）

[23]Mei F X 1994 Acta.Mech.Sinica.26 470.（in Chinese）

责任编辑：陈侃

*Received March 17,2010

Project supported by the National Natural Science Foundation of China under Grant No.10872037 and the National Natural Science Foundation of Anhui Province under Grant No.070416226.

Biography:Zhang Hong-Bin(1963-),Male,Doctor,Professor.